「实战案例」基于Python语言开发的信用评分卡

信用风险计量模型可以包括跟个人信用评级，企业信用评级和国家信用评级。人信用评级有一系列评级模型组成，常见是A卡（申请评分卡）、B卡（行为模型）、C卡（催收模型）和F卡（反欺诈模型）。 今天我们展示的是个人信用评级模型的开发过程，数据采用kaggle上知名的give me some credit数据集。
今天，给各位数据粉带来的是比较熟悉的一个经典数据挖掘应用案例——金融常见信用评分卡的开发解析。

基于Python语言开发信用评分卡

Part 1 学会信用评分卡，我都能干什么？

01、信用评分卡的应用场景

与信用评分卡挂钩的信用评级在全球金融领域有广泛应用。它涉及到公司管理，企业债发行，企业融资，企业上市，企业并购，个人炒股和购买公司债券等多个场景。

企业债发行

企业主体信用评级越高，意味着该企业抗风险能力、盈利能力越强，发债融资成本越低。作为企业董事会，管理者，决策者应该了解企业主要财务指标，了解自身企业评级。

企业发债时都需要评级。国内评级这块主要分为AAA、AA+、AA、AA-、A+。企业评级过低会限制某些工具的发行额度、交易场所可质押性等等

如果是评级太低，企业发行债券没人买。目前广大投资者的投资门槛是AA。

企业上市

企业上市融资时也需要信用评级。目前国内只有优质企业才能上市融资，上市牌照是很难拿的。如果财务指标和资质不达标，则不能上市。

企业并购

企业并购是企业之间的兼并和收购行为。如果收购方不能很好了解对方企业评级，买来的企业可能是包装过的垃圾企业。失败企业并购会让企业背上巨大债务负担。

个人炒股

个人炒股投资者如果不懂企业评级，也难以买到优质股，容易被人忽悠买到垃圾股。建议不会数据科学的人趁早离开股市和金融投资，否则可能欠下巨额债务。

如果个人通过学习机器学习模型，可以识别有价值企业，股票，债券，财富升值概率显著高于不懂模型的人。

本案我们主要聚焦的是【金融信贷】场景中的信用评分卡开发实施全过程。

评分卡模型建模流程

典型的信用评分卡模型如图1-1所示。信用风险评级模型的主要开发流程如下：
（1） 获取数据，包括申请贷款客户的数据。数据包括客户各个维度，包括年龄，性别，收入，职业，家人数量，住房情况，消费情况，债务等等。
（2） 数据预处理，主要工作包括数据清洗、缺失值处理、异常值处理、数据类型转换等等。我们需要把原始数据层层转化为可建模数据。
（3） EDA探索性数据分析和描述性统计，包括统计总体数据量大小，好坏客户占比，数据类型有哪些，变量缺失率，变量频率分析直方图可视化，箱形图可视化，变量相关性可视化等。
（4） 变量选择，通过统计学和机器学习的方法，筛选出对违约状态影响最显著的变量。常见变量选择方法很多，包括iv，feature importance，方差等等 。另外缺失率太高的变量也建议删除。无业务解释性变量且没有价值变量也建议删除。
（5） 模型开发，评分卡建模主要难点是woe分箱，分数拉伸，变量系数计算。其中woe分箱是评分卡中难点中难点，需要丰富统计学知识和业务经验。目前分箱算法多达50多种，没有统一金标准，一般是先机器自动分箱，然后再手动调整分箱，最后反复测试模型最后性能，择优选取最优分箱算法。
（6） 模型验证，核实模型的区分能力、预测能力、稳定性、排序能力等等，并形成模型评估报告，得出模型是否可以使用的结论。模型验证不是一次性完成，而是当建模后，模型上线前，模型上线后定期验证。模型开发和维护是一个循环周期，不是一次完成。
（7） 信用评分卡，根据逻辑回归的变量系数和WOE值来生成评分卡。评分卡方便业务解释，已使用几十年，非常稳定，深受金融行业喜爱。其方法就是将Logistic模型概率分转换为300-900分的标准评分的形式。
（8） 建立评分卡模型系统，根据信用评分卡方法，建立计算机自动信用化评分系统。美国传统产品FICO有类似功能，FICO底层语言是Java。目前流行Java，python或R多种语言构建评分卡自动化模型系统。

（9）模型监控，着时间推移，模型区分能力，例如ks,auc会逐步下降，模型稳定性也会发生偏移。我们需要专业模型监控团队，当监控到模型区分能力下降显著或模型稳定性发生较大偏移时，我们需要重新开发模型，迭代模型。模型监控团队应该每日按时邮件发送模型监控报表给相关团队，特别是开发团队和业务团队。

02、金融信贷基础概念

在进行项目实施开发前，对应用场景进行深入了解，是我们数据人的基本功。

信用风险

信贷业务，又称贷款业务，是商业银行等信贷机构最重要的资产业务和主要赢利手段。信贷机构通过放款收回本金和利息，扣除成本后获得利润。对有贷款需求的用户，信贷机构首先要对其未来的还款表现进行预测，然后将本金借贷给还款概率大的用户。但这种借贷关系，可能发生信贷机构（通常是银行）无法收回所欠本金和利息而导致现金流中断和回款成本增加的可能性风险，这就是信用风险，它是金融风险的主要类型。

信用评分

在信贷管理领域，关于客户信用风险的预测，目前使用最普遍的工具为信用评分卡，它源于20世纪的银行与信用卡中心。在最开始的审批过程中，用户的信用等级由银行聘用的专家进行主观评判。而随着数据分析工具的发展、量化手段的进步，各大银行机构逐渐使用统计模型将专家的评判标准转化为评分卡模型。如今，风险量化手段早已不局限于银行等传统借贷机构，持牌互联网公司的金融部门、持牌消费金融公司等均有成体系的风险量化手段。其应用的范围包括进件、贷后管理及催收等。信用评分不但可以筛选高风险客户，减少损失发生，也可以找出相对优质的客户群，发掘潜在商机。

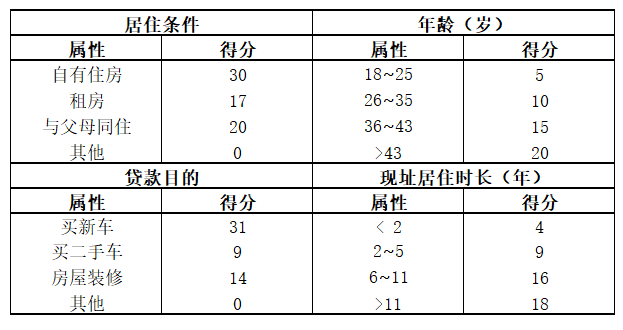
顾名思义，评分卡是一张有分数刻度和相应阈值的表。对于任何一个用户，总能根据其信息找到对应的分数。将不同类别的分数进行汇总，就可以得到用户的总分数。信用评分卡，即专门用来评估用户信用的一张刻度表，这里我们举一个简单的例子：假设我们有一个评分卡，包含四个变量（特征），即居住条件、年龄、贷款目的和现址居住时长（见表2-1）

表2-1 简单评分卡

用表2-1这张简单的评分卡，我们能轻而易举地计算得分。一个47岁、租房、在当前住址住了10年、想借钱度假的申请者得到53分（20+17+16+0=53），另一个25岁、有自己的房产、在当前住址住了2年、想借钱买二手车的人也同样得到53分（5+30+9+9=53）。同样地，一个38岁、与父母同住、在当前住址住了18个月、想借钱装修的人也得到53分（15+20+4+14=53）。事实上，我们一共有七个组合可以得到53分，他们虽然各自情况都不一样，但对贷款机构来说代表了同样的风险水平。该评分系统采用了补偿机制，即借款人的缺点可以用优点去弥补。

总的来说，信用评分卡就是通过用数据对客户还款能力和还款意愿进行定量评估的系统。从20世纪发展至今，其种类已非常多，目前应用最广泛最多的主要分为以下四种：

• 申请评分卡（ApplicationCard）：申请评分卡通常用于贷前客户的进件审批。在没有历史平台表现的客群中，外部征信数据及用户的资产质量数据通常是影响客户申请评分的主要因素。
• 行为评分卡（BehaviorCard）：行为评分卡用于贷中客户的升降额度管理，主要目的是预测客户的动态风险。由于客户在平台上已有历史数据，通常客户在该平台的历史表现对行为评分卡的影响最大。
• 催收评分卡（CollectionCard）：催收评分卡一般用于贷后管理，主要使用催收记录作为数据进行建模。通过催收评分对用户制定不同的贷后管理策略，从而实现催收人员的合理配置。
• 反欺诈评分卡（Anti-fraudCard）：反欺诈评分卡通常用于贷前新客户可能存在的欺诈行为的预测管理，适用于个人和机构融资主体。

其中前三种就是我们俗称的“ABC”卡。A卡一般可做贷款0-1年的信用分析；B卡则是在申请人一定行为后，有了较大消费行为数据后的分析，一般为3-5年；C卡则对数据要求更大，需加入催收后客户反应等属性数据。

四种评分卡中，最重要的就是申请评分卡，目的是把风险控制在贷前的状态；也就是减少交易对手未能履行约定契约中的义务而造成经济损失的风险。违约风险包括了个人违约、公司违约、主权违约，本案例只讲个人违约。

案例背景

发放贷款给合适的客户是银行收入的一大来源，在条件允许的范围内，银行希望贷出去的钱越多越好，贷款多意味着对应的收入也多，但是如果把钱贷给了信用不好的人或者企业，就会面临贷款收不回来的情况。

对于贷款申请的审批，传统人工审批除了受审批人员的专业度影响外，也会受到其主观影响，另一方面专业人员的培养通常也需要一个较长的周期。 而信用评分卡技术的变量、评分标准和权重都是给定的。同一笔业务，只要录入要素相同，就会给出一个参考结果。既提高了审批效率也减少了人为因素的干扰，如人工审批过程中的随意性和不一致性。确保了贷款审批标准的客观性、标准化和一致性；保证风险特征相近的贷款申请能够得到相似的审批结果，如审批通过与否、授信额度、利率水平等。

信用评分卡技术在20世纪50年代即广泛应用于消费信贷，尤其是在信用卡领域。随着信息技术的发展和数据的丰富，信用评分卡技术也被用于对小微企业贷款的评估，最初是拥有大量客户数据信息的大型银行。如富国银行1993年首先在小微企业贷款领域应用信用评分卡技术。随后，美国很多社区银行等中小银行也开始广泛应用小微企业信用评分系统。

现中国的某银行信用卡中心的贷款申请业务近期又增长了10%，原来的申请评分卡已出现数据偏移，监测到审批准确度有下降趋势。作为信用卡中心的风控建模分析师，小王接到风控总监下发的任务：基于近两年的历史数据（见“数据集介绍”的Train_data.csv），重新建立一张“申请评分卡”用于预测申请者未来是否会发生90天以上的逾期行为，以此来判断给哪些客户予以发放，哪些客户予以拒绝。

数据集介绍

• 训练数据：Train_data.csv。该数据即有特征X又有标签y，是小王用来建模的数据。
• 预测数据：Predict_data.csv。该数据只有特征X没有标签y，为小王需要预测的数据。也即新进的申请信用卡的客户相关信息。

基于Python语言开发信用评分卡

Part 2 信用评分卡如何做数据准备工作

导入相关依赖模块

# 加载所需包

%matplotlib inline

import matplotlib.pyplot as plt

import numpy as np

import pandas as pd

import os

import woe.feature_process as fp

import woe.eval as eval

from collections import Counter

from sklearn.model_selection import train_test_split

import seaborn as sns

plt.rc(‘font’, family=‘SimHei’, size=13) # 显示中文

plt.rcParams[‘axes.unicode_minus’] = False # 用来正常显示负

import sys

sys.path.append(‘E:\大数据实验室_教研部案例集\自定义函数’) # 添加自定义函数文件所在的环境路径

from summary_df import data_summary #用于数据探查

from score_scale import score_scale

from score_predict import score_predict

数据探索

os.chdir(r"E:\大数据实验室_教研部案例集\案例1_信用评分卡\data")

data_org = pd.read_csv(“Train_data.csv”)

data_summary(data_org)

数据准备

数据清洗-ALL数据

data_org.drop_duplicates(inplace=True)

#data_org.shape

#(149391, 11)

• 可见数据中存在重复行。

a = Counter(data_org[‘Label’])

print(“原数据集的正负样本量为：”,a)

print(“原数据集好坏样本的比例为：{:.5f}”.format(a[0]/a[1]))

原数据集的正负样本量为： Counter({0: 139382, 1: 10009})

原数据集好坏样本的比例为：13.92567

• result: 我们知道一般建模所需的好坏客户样本比率约为3:1～5:1。评分卡建模通常要求正负样本的数量都不少于1500个。但样本量也并非越大越好，当总样本量超过50000个时，模型的效果将不再随着样本量的增加而有显著变化了，而且数据处理与模型训练过程也较为耗时。
• 这里我们需要对样本做欠采样（Subsampling）:
• 负样本取10000条
• 正样本取40000条

数据筛选与数据平衡

from sklearn.utils import shuffle

data_org = shuffle(data_org) # 全体数据做随机打乱

data_bad = data_org[data_org[‘Label’]==1] # 坏客户

data_good = data_org[data_org[‘Label’]==0] # 好客户

data_bad_select = data_bad.iloc[:10000,:] #选前10000条坏客户

data_good_select = data_good.iloc[:40000,:] #选前40000条好客户

data_select = pd.concat([data_bad_select,data_good_select]) #最终数据

# data_select.shape

#(50000, 11)

拆分训练集和测试集

from sklearn.model_selection import train_test_split

from collections import Counter

# 数据提取与数据分割

X = data_select.drop([‘Label’],axis=1) # 特征列

y = data_select[‘Label’] # 标签列

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,random_state=0)

print(“训练集正负样本数据量：{}”.format(Counter(y_train)))

print(“测试集正负样本数据量：{}”.format(Counter(y_test)))

训练集正负样本数据量：Counter({0: 28017, 1: 6983})

测试集正负样本数据量：Counter({0: 11983, 1: 3017})

数据清洗-训练数据

缺失值处理

查看缺失值分布情况

import missingno as msno # 处理缺失值的包,需要安装

msno.matrix(X_train)

plt.show()

plt.imshow(~X_train.isna(),aspect=“auto”)

plt.gray()

缺失值处理的常用方法：

缺失值处理方法的选择,主要依据是业务逻辑和缺失值占比,在对预测结果的影响尽可能小的情况下,对缺失值进行处理以满足算法需求,所以要理解每个缺失值处理方法带来的影响,下面的缺失值处理方法没有特殊说明均是对特征(列)的处理:

1. 占比较多:如80%以上,直接删除该变量

• 如果某些行缺失值占比较多,或者缺失值所在字段是苛刻的必须有值的,删除行

1. 占比一般:如30%-80%:将缺失值作为单独的一个分类

• 如果特征是连续的,则其他已有值分箱
• 如果特征是分类的,考虑其他分类是否需要重分箱

1. 占比少:10%-30%:多重插补:认为若干特征之间有相关性,则可以相互预测缺失值

• 需满足的假设:MAR:Missing At Random:数据缺失的概率仅和已观测的数据相关,即缺失的概率与未知的数据无关,即与变量的具体数值无关
• 迭代(循环)次数可能的话超过40,选择所有的变量甚至额外的辅助变量
• 详细的计算过程参考:Multiple Imputation by Chained Equations: What is it and how does it work?

1. 占比较少:10%以下，单一值替换,如中位数,众数，或者从业务理解上用0值、特殊值填充
2. 在决策树中可以将缺失值处理融合到算法里:按比重分配

这里的占比并不是固定的,例如缺失值占比只有5%,仍可以用第二种方法,主要依据业务逻辑和算法需求

本数据的缺失值处理逻辑:

• 对于信用评分卡来说,由于所有变量都需要分箱,故这里缺失值作为单独的箱子即可
• 对于最后一列Dependents,缺失值占比只有2.56%,作为单独的箱子信息不够,故做单一值填补,这列表示家庭人口数,有右偏的倾向,且属于计数的数据,故使用中位数填补
• 这里没必要进行多重插补,下面的多重插补只是为了让读者熟悉此操作

单一值替换填充缺失值

# Dependents的缺失值用其中位数替换

NOD_median = X_train[“Dependents”].median()

X_train[“Dependents”].fillna(NOD_median,inplace=True) # fillna填补缺失值的函数,这里用中位数填补

X_train[“Dependents”].fillna(NOD_median,inplace=True) # 对测试集填充缺失值

#MonthlyIncome 列的缺失值超过5%，可作为单独的一个分类处理。这里统一将赋值为-8

X_train[“MonthlyIncome”].fillna(-8,inplace=True)

X_train[“MonthlyIncome”].fillna(-8,inplace=True)

C:\Anaconda3\lib\site-packages\pandas\core\generic.py:6287: SettingWithCopyWarning:

A value is trying to be set on a copy of a slice from a DataFrame

See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy

self._update_inplace(new_data)

check数据是否还有缺失值

a = data_summary(X_train)

data_missing_summary = a[a[‘percent’]<1]

if

data_missing_summary.shape[0]==0:

print(‘数据已经没有缺失值！’)

else:

print(‘数据还存在缺失值，请输出数据框data_missing_summary查看缺失情况！’)

数据已经没有缺失值！

异常值处理

异常值处理的常用方法:

1. 删除对应的样本数据，即所在的行
2. 替换成缺失值,当缺失值处理
3. 盖帽法处理

结合业务逻辑和算法需求判断是否需要处理异常值以及如何处理,一般情况下盖帽法即可,即将极端异常的值改成不那么异常的极值。不过一些算法例如决策树中连续变量的异常值也可以不做处理。

自定义盖帽法函数

盖帽法将某连续变量均值上下三倍标准差范围外的记录替换为均值上下三倍标准差值，即盖帽处理。

def cap(x,lower=True,upper=True):

“”"

函数功能：盖帽法处理异常值。

参数解释：

x： 表示输入的Series对象

lower：表示是否替换1%分位数

upper：表示是否替换99%分位数

“”"

# 生成分位数:1%和99%的分位数

quantile = [0.01,0.99]

Q01,Q99=x.quantile(quantile).values.tolist()

#替换异常值为指定的分位数

if lower:

out = x.mask(x

if upper:

out = x.mask(x>Q99,Q99)

return(x)

# 先保留原数据X_train盖帽法中的极端值，以备后面训练集和预测集处理其异常值时使用

df_min_max = X_train.apply(lambda x:x.quantile([0.01,0.99]))

#盖帽法处理异常值

X_train = X_train.apply(cap)

data_summary(X_train)

数据清洗-测试集数据

# 用训练的信息填充

X_test[“Dependents”].fillna(NOD_median,inplace=True) # 对测试集填充缺失值

X_test[“MonthlyIncome”].fillna(-8,inplace=True)

def cap2(x,df_min_max,lower=True,upper=True):

“”"

函数功能：用训练集中的盖帽法极端值处理测试集的异常值。

参数解释：

x： 表示输入的Series对象；

df_min_max：是训练集中的盖帽法极端值数据框。

“”"

col_name = x.name

Q01,Q99 = df_min_max[col_name].values

#替换异常值为指定的分位数

if lower:

out = x.mask(x

if upper:

out = x.mask(x>Q99,Q99)

return(x)

# 用训练集中的盖帽法极端值处理测试集的异常值

for itr in df_min_max.columns:

X_test[itr] = cap2(X_test[itr],df_min_max)

# 合并数据X,Y

data_train = pd.concat([X_train,y_train],axis=1)

data_test = pd.concat([X_test,y_test],axis=1)

训练数据特征处理

WOE分箱

我们要制作评分卡，最终想要得到的结果是要给各个特征进⾏分档，以便业务⼈员能够根据新客户填写的信息为客户打分。我们知道变量（即特征）的形态可分为离散型和连续型，离散型天然就是分档的，因此，我们需要重点如何使连续变量分档，即连续变量离散化。

连续变量离散化，我们也常称为分箱或者分组操作。它是评分卡制作过程中⼀个非常重要的步骤，是评分卡最难，也是最核⼼的思路。目的就是使拥有不同属性的客户被分成不同的类别，进而评上不同的分数。在评分卡建模流程中，我们常用WOE（Weight of Evidence，迹象权数）方法对变量进行分箱。

WOE分箱的好处：

• 避免变量值中出现极端值（Outliers）的情形，
• 减少模型过度配适（Overfitting）的现象。

Python代码实现woe

“”"

woe分箱, iv and transform:

woe包的使用条件：因变量y的列名必须为"target",列值必须为0或1.

“”"

data_train.rename(columns={‘Label’: ‘target’}, inplace=True) # 修改列名为"target"

civ_dict ={}

all_cnt = len(data_train) # 所有样本数据量

n_positive = sum(data_train[‘target’]) # 正样本数据量

n_negtive = all_cnt - n_positive # 负样本数据量

for column in set(data_train.columns)-set([“target”]):

if data_train[column].dtypes == ‘object’:

civ = fp.proc_woe_discrete(data_train, column, n_positive, n_negtive, 0.05*all_cnt, alpha=0.02)

else:

civ = fp.proc_woe_continuous(data_train, column, n_positive, n_negtive, 0.05*all_cnt, alpha=0.02)

civ_dict[column]=civ

--------------process continuous variable:Age---------------

-----------process continuous variable:Dependents-----------

-------process continuous variable:OverDue_60_89days--------

---------process continuous variable:OverDue_90days---------

----------process continuous variable:CreditLoans-----------

-----------process continuous variable:DebtRatio------------

-------process continuous variable:OverDue_30_59days--------

---------process continuous variable:MortgageLoans----------

-----process continuous variable:AvailableBalanceRatio------

---------process continuous variable:MonthlyIncome----------

变量的IV值

用与之相关的另一个重要概念，IV值（Information Value，信息值）则用来衡量该变量（特征）对好坏客户的预测能力。

查看每个变量对应的IV值

civ_df = eval.eval_feature_detail(list(civ_dict.values()),out_path=’

output_feature_detail_20210218.csv’) # 输出分箱结果

# 整理输出每个变量的IV值

iv_result_a = civ_df[[‘var_name’,‘iv’]].drop_duplicates()

iv_result = iv_result_a[‘iv’]

iv_result.index = iv_result_a[‘var_name’].values

Age

Dependents

OverDue_60_89days

OverDue_90days

CreditLoans

DebtRatio

OverDue_30_59days

MortgageLoans

AvailableBalanceRatio

MonthlyIncome

# 查看每个变量的IV值

iv_result.sort_values().plot(kind=“barh”)

iv_result.sort_values(ascending=False)

AvailableBalanceRatio 1.173317

OverDue_90days 0.845325

OverDue_30_59days 0.723239

OverDue_60_89days 0.574336

MonthlyIncome 0.084926

DebtRatio 0.082108

CreditLoans 0.073128

Age 0.063129

MortgageLoans 0.054396

Dependents 0.035709

Name: iv, dtype: float64

• 可见所有的IV值均大于0.02,故这里使用所有变量

# 删除iv值过小的变量

iv_thre = 0.02 #阈值设置为0.02

keep_vars_iv = iv_result[iv_result > iv_thre]# 筛选出iv值（大于阈值）有辨别能力的变量

keep_vars_iv

Age 0.063129

Dependents 0.035709

OverDue_60_89days 0.574336

OverDue_90days 0.845325

CreditLoans 0.073128

DebtRatio 0.082108

OverDue_30_59days 0.723239

MortgageLoans 0.054396

AvailableBalanceRatio 1.173317

MonthlyIncome 0.084926

Name: iv, dtype: float64

相关系数热力图

通过变量直接的相关性系数，建立相关性矩阵，观察变量之间的关系，可以进行初步的多重共线性筛选。

全部变量的相关信息热力图

p_corr = data_train.corr() # 相关系数矩阵，对称矩阵

p_corr_tril = np.tril(p_corr,0) # 因此取下三角矩阵

label_col = p_corr.columns

res= pd.DataFrame(p_corr_tril,columns=label_col,index=label_col)

sns.heatmap(res,cmap=‘Blues’);

部分变量相关度（>threshold）热力图

#只相关系数较高的值，比如大于threshold以上的值

threshold = 0.75 # 阈值，通常取0.75,0.8附近的值

p_corr_tril[p_corr_tril<=threshold]=0.01 # 相关度小于threshold的值都置为0.01

label_col = p_corr.columns

res2= pd.DataFrame(p_corr_tril,columns=label_col,index=label_col)

sns.heatmap(res2,cmap=‘Blues’);

# 查看iv值

col=[‘OverDue_30_59days’,‘OverDue_60_89days’, ‘OverDue_90days’]

keep_vars_iv.loc[col]

OverDue_30_59days 0.723239

OverDue_60_89days 0.574336

OverDue_90days 0.845325

Name: iv, dtype: float64

• 可以卡看出’OverDue3059days’,‘OverDue6089days’, ‘OverDue90days’这三个变量之间具有非常高的相关度。为剔除多重共线性的影响，我们这里只保留IV值最大的变量’OverDue90days’，删除’OverDue3059days’,‘OverDue6089days’。

# 经过IV值和相关度筛选后保留的变量

keep_vars = set(keep_vars_iv.index) - {‘OverDue_30_59days’,‘OverDue_60_89days’}

训练集和测试集WOE特征转换

keep_var_woe={} # 筛选后保留的变量{变量名：变量名_woe}

for i in keep_vars:

keep_var_woe[i] = i+’_woe’

#WOE特征转换

for var_name,var_woe in keep_var_woe.items():

data_train[var_woe] = fp.woe_trans(data_train[var_name], civ_dict[var_name])

data_test[var_woe] = fp.woe_trans(data_test[var_name], civ_dict[var_name])

X_train_woe = data_train[keep_var_woe.values()] # train集的WOE特征

X_test_woe = data_test[keep_var_woe.values()] # test集的WOE特征

print(“训练集经过WOE转换后的shape：{}”.format(X_train_woe.shape))

print(“测试集经过WOE转换后的shape：{}”.format(X_test_woe.shape))

训练集经过WOE转换后的shape：(35000, 8)

测试集经过WOE转换后的shape：(15000, 8)

基于Python语言开发信用评分卡

Part3 信用评分卡模型构建

逻辑回归建模

网格调参

from sklearn.linear_model import LogisticRegression

from sklearn.model_selection import GridSearchCV

cv_params ={ ‘C’: np.arange(0.1,1,0.1),

‘penalty’: [‘l1’, ‘l2’, ‘elasticnet’, ‘none’],

‘solver’: [‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’]

}

model = LogisticRegression()

gs = GridSearchCV(estimator=model,

param_grid=cv_params,

scoring=‘roc_auc’,

cv=5,

verbose=1,

n_jobs=4)

gs.fit(X_train_woe,y_train)

print(‘测试集得分:{0}’.format(gs.score(X_test_woe,y_test)))

# print(‘每轮迭代运行结果:{0}’.format(grid_search.scorer_))

print(‘参数的最佳取值:{0}’.format(gs.best_params_))

print(‘最佳模型得分:{0}’.format(gs.best_score_))

Fitting 5 folds for each of 180 candidates, totalling 900 fits

测试集得分:0.8223083325618374

参数的最佳取值:{‘C’: 0.4, ‘penalty’: ‘l2’, ‘solver’: ‘liblinear’}

最佳模型得分:0.8295380458229852

建模

from sklearn.linear_model import LogisticRegression

other_params = {‘C’: 0.4, ‘penalty’: ‘l2’, ‘solver’: ‘liblinear’}

LR_model = LogisticRegression(**other_params)

LR_model.fit(X_train_woe, y_train)

print(“变量名：\n”,list(keep_var_woe.keys()))

print(“各个变量系数：\n”,LR_model.coef_)

print(“常数项：\n”,LR_model.intercept_)

变量名：

[‘Age’, ‘Dependents’, ‘CreditLoans’, ‘DebtRatio’, ‘OverDue_90days’, ‘MortgageLoans’, ‘AvailableBalanceRatio’, ‘MonthlyIncome’]

各个变量系数：

[[ 0.32460639 0.60488285 -0.25729929 0.84472115 0.73975662 0.54027275

0.7871042 0.16668148]]

常数项：

[-1.37892239]

模型评估

模型的评价指标一般有Gini系数、K-S值和AUC值，基本上都是基于评分卡分数的。但是从理论上评分分数是依据预测为正样本的概率计算而得，因此基于这个概率计算的指标也是成立的。

下面我们用sklearn库中的函数计算模型的AUC值和K-S值，以此初步判断模型的优劣。

from sklearn.metrics import confusion_matrix,roc_auc_score,roc_curve, auc,precision_recall_curve

y_pred_train = LR_model.predict(X_train_woe)

y_pred_test = LR_model.predict(X_test_woe)

训练集的混淆矩阵：

[[27141 876]

[ 4657 2326]]

测试集的混淆矩阵：

[[11598 385]

[ 2032 985]]

# 预测的分值

y_score_train = LR_model.predict_proba(X_train_woe)[:,1] # 通过 LR_model.classes_ 查看哪列是label=1的值

y_score_test = LR_model.predict_proba(X_test_woe)[:,1]

# 分别计算训练集和测试集的fpr,tpr,thresholds

train_index = roc_curve(y_train, y_score_train) #计算fpr,tpr,thresholds

test_index = roc_curve(y_test, y_score_test) #计算fpr,tpr,thresholds

AUC值

ROC曲线是以在所有可能的截断点分数下，计算出来的对评分模型的误授率（误授率表示模型将违约客户误评为好客户，进行授信业务的比率）和1-误拒率（误拒率表示模型将正常客户误评为坏客户，拒绝其授信业务的比率）的数量所绘制而成的，AUC值为ROC曲线下方的总面积

# AUC值

roc_auc_train = roc_auc_score(y_train, y_score_train)

roc_auc_test = roc_auc_score(y_test, y_score_test)

print(‘训练集的AUC:’, roc_auc_train)

print(‘测试集的AUC:’, roc_auc_test)

训练集的AUC: 0.8297773383440796

测试集的AUC: 0.8223083325618374

• 训练集和测试集的AUC值相差不大，没有发生过拟合的情况

我们再绘制训练集的ROC曲线与测试集的ROC曲线

KS曲线

K-S 测试图用来评估评分卡在哪个评分区间能够将正常客户与违约客户分开。根据各评分分数下好坏客户的累计占比，就可完成K-S测试图。

print(“训练集的KS值为：{}”.format(max(train_index[1]-train_index[0])))

print(“测试集的KS值为：{}”.format(max(test_index[1]-test_index[0])))

训练集的KS值为：0.5117269204064546

测试集的KS值为：0.5067980932328976

# ------------------------- KS 曲线

---------------------------

绘制训练集与测试集的KS曲线

result: 从AUC值和K-S值来看，我们训练的模型对好坏客户已经具有非常良好的区辨能力了。并且训练集和测试集指标接近，没有发生过拟合的情况。

需要注意的是实际业务中数据需要这样准备：模型开发前，我们一般会将数据分为：训练集train、测试集test、跨时间数据OOT（train和test是同一时间段数据，一般三七分，oot是不同时间段的数据，用来验证模型是否适用未来场景）通过这样的技术保证模型最终可靠稳定。

生成评分卡

评分卡输出

# 用自定义的评分卡函数score_scale生成评分卡，参数可见具体的函数

r=score_scale(LR_model,X_train_woe,civ_df,pdo=20,score=600,odds=10)

# 输出最终的评分卡

r.ScoreCard.to_excel(“ScoreCard.xlsx”,index=False)

print(“评分卡最大值和最小值区间为：{}”.format(r.minmaxscore))

评分卡最大值和最小值区间为：[447, 640]

基于评分的KS值

绘制结果如下：

策略建议

由训练集的KS值可知，570分是好坏样本的最佳分隔点。测试集对其进行验证，KS值为569,基本一致。因此我们可在训练集的KS值上下10分内可做如下策略：

• 580分以上的直接予以通过；
• 560分以上的直接予以拒绝；
• [560,580]之间的人群，可以加入人工判断进行审核。

以上只是我们给出的策略建议，实际问题和需求远比这里复杂，风控人员可以根据具体业务需求给出更加贴合实际业务的策略建议。

新数据的预测

数据准备

# 读取预测数据

data_predict = pd.read_csv(“Predict_data.csv”)

# 缺失值的处理

data_predict[“Dependents”].fillna(NOD_median,inplace=True) #用训练集填信息充缺失值

data_predict[“MonthlyIncome”].fillna(-8,inplace=True)

# 异常值的处理：用训练集中的盖帽法极端值处理预测集的异常值

for itr in df_min_max.columns:

data_predict[itr] = cap2(data_predict[itr],df_min_max)

# WOE特征转换

for var_name,var_woe in keep_var_woe.items():

data_predict[var_woe] = fp.woe_trans(data_predict[var_name], civ_dict[var_name])

X_predict_woe = data_predict[keep_var_woe.values()] # train集的WOE特征

print(“用于预测的数据集经过WOE转换后的shape：{}”.format(X_predict_woe.shape))

用于预测的数据集经过WOE转换后的shape：(101503, 8)

预测

# 预测客户的评分结果

score_result = score_predict(data_predict,r)

# 预测为正样本的概率

X_predict_woe = data_predict[keep_var_woe.values()]

# 合并评分和概率

y_score_predict = LR_model.predict_proba(X_predict_woe)[:,1] # 通过 LR_model.classes_ 查看哪列是label=1的值

y_score_predict = pd.Series(y_score_predict).to_frame(name=‘预测为违约客户的概率’)

# 保留用户ID、预测评分和预测概率三列信息，并输出

data_predict_score = score_result[[‘UserID’,‘Score’]].rename(columns={‘Score’:‘预测评分’})

predict_result = pd.concat([data_predict_score,y_score_predict],axis=1)

# 生成“策略建议”策列

cut_off = 570 #切分值

f = 10 #上下浮动值

fuc = lambda x:‘通过’ if x>cut_off+f else ‘拒绝’ if x

predict_result[‘策略建议’] = predict_result[‘预测评分’].map(fuc)

predict_result.to_excel(“predict_result.xlsx”,index=False)# 输出预测结果to excel

predict_result.head(20) #查看前20行

predict_result.groupby(‘策略建议’).size().to_frame(name=‘人数统计’)

• Result: 这里银行原本需要审批的客户量有105103（=13747+21049+66707。这里经过小王的模型策略，需要人工介入审核的客户量降为13747，只占全部的13.08%。而其中86.92%的客户都能自动决策是通过还是拒绝。

结束语

至此，我们已经用python实现了一个申请评分卡的开发过程，并在结尾给出了策略建议。数据化后的风控极大提高了银行的审批效率，这是传统的人工审核不可比拟的，也正是大数据时代带给我们的便利。另外需要注意的是，在实际中，模型上线还需要持续追踪模型的表现，一般是每个月月初给全量客户打分，并生成前端和后端监控报告。基于Python的信用评分卡模型主要流程就为大家介绍到这里，但实操评分卡建模中有很多细节，互联网上对这些细节描述过于草率甚至不正确。例如变量缺失率达到80%-90%就应该直接删除该变量吗？变量相关性高达0.8就可以去掉吗？经验丰富建模人员需要在数学理论，业务线实际需求，计算机测试结果等多方面找到平衡点，而不是只从一个角度思考问题。这就像经验丰富外科医生并不一定完全遵循教科书的理论。统计学，机器学习，人工智能等领域里有很多争议地方，并非有完全统一共识。各位在学习时要保持独立思考能力，这样才能不断优化数据科学知识。

基于Python的信用评分卡模型-give me some credit就为大家介绍到这里了，欢迎各位同学报名,学习更多相关知识
https://edu.csdn.net/combo/detail/1927

版权声明：文章来自公众号(python风控模型),未经许可，不得抄袭。遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。