从零开始学习线性回归:理论、实践与PyTorch实现
文章目录
- 介绍
- 基本知识
- 代码实现
- 完整代码
- 总结
介绍
线性回归是统计学和机器学习中最简单而强大的算法之一,用于建模和预测连续性数值输出与输入特征之间的关系。本博客将深入探讨线性回归的理论基础、数学公式以及如何使用PyTorch实现一个简单的线性回归模型。
基本知识
线性回归的数学基础
线性回归的核心思想是建立一个线性方程,它表示了自变量(输入特征)与因变量(输出)之间的关系。这个线性方程通常表示为:

其中, y y y 是因变量, x 1 , x 2 , … , x p x_1, x_2, \ldots, x_p x1,x2,…,xp 是自变量, b 0 , b 1 , b 2 , … , b p b_0, b_1, b_2, \ldots, b_p b0,b1,b2,…,bp 是模型的参数, p p p 是特征的数量。我们的目标是找到最佳的参数值,以最小化模型的误差。
损失函数
为了找到最佳参数,我们需要定义一个损失函数来度量模型的性能。在线性回归中,最常用的损失函数是均方误差(MSE),它表示了模型预测值与实际值之间的平方差的平均值:

其中, n n n 是样本数量, y i y_i yi 是实际值, y ^ i \hat{y}_i y^i 是模型的预测值。
梯度下降优化
为了最小化损失函数,我们使用梯度下降算法。梯度下降通过计算损失函数相对于参数的梯度,并迭代地更新参数,以减小损失。更新规则如下:
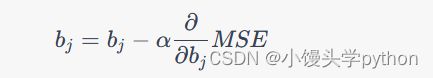
其中, b j b_j bj 是第 j j j个参数, α \alpha α 是学习率, ∂ ∂ b j M S E \frac{\partial}{\partial b_j} MSE ∂bj∂MSE 是损失函数对参数 b j b_j bj的偏导数。
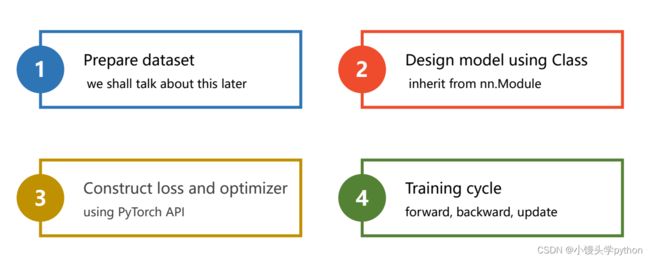
代码实现
- 准备数据
- 设计模型(计算) y ^ i \hat{y}_i y^i
- 构造损失和优化器
- 训练周期(前向,反向 ,更新)
本节还是以刘二大人的视频讲解为例,结尾会设置传送门
class LinearModel(torch.nn.Module):
def __init__(self):
super(LinearModel, self).__init__() # 调用父类的构造函数
self.linear = torch.nn.Linear(1, 1) # 参数详情下图展示
def forward(self, x):
y_pred = self.linear(x) # x代表输入样本的张量
return y_pred
model = LinearModel()
所以模型类都要继承Module,此类主要包含两个函数一个是构造函数(初始化对象时调用),另一个是前向计算
好奇的小伙伴会思考为何没有反向(backward),这是因为Module会帮你进行,但是如果后期自己有更高效的方法可以自行设置。

-
第一个参数 in_features:这是输入特征的数量。在这里,表示我们的模型只有一个输入特征。如果你有多个输入特征,你可以将这个参数设置为输入特征的数量。
-
第二个参数 out_features:这是输出特征的数量。这表示我们的模型将生成一个输出。在线性回归中,通常只有一个输出,因为我们试图预测一个连续的数值。
-
第三个参数:意思是要不要偏置量。默认true
通常情况下特征代表列,比如我们有一个n×2的y和一个n×3的x,那么我们需要一个3×2的权重,有的书中会在两边做转置,但无论咋样目的都是为了让这个矩阵乘法成立
criterion = torch.nn.MSELoss(size_average=False) # 使用均方误差损失
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # 使用随机梯度下降优化器


model.parameters() 用于告诉优化器哪些参数需要在训练过程中进行更新,这包括模型的权重和偏置项等。在线性回归示例中,模型的参数包括权重和偏置项。
之后就进行训练了
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad() # 归零
loss.backward() # 反向
optimizer.step() # 更新
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)
完整代码
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[2.0], [4.0], [6.0]])
class LinearModel(torch.nn.Module):
def __init__(self):
super(LinearModel, self).__init__()
self.linear = torch.nn.Linear(1, 1)
def forward(self, x):
y_pred = self.linear(x)
return y_pred
model = LinearModel()
criterion = torch.nn.MSELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)
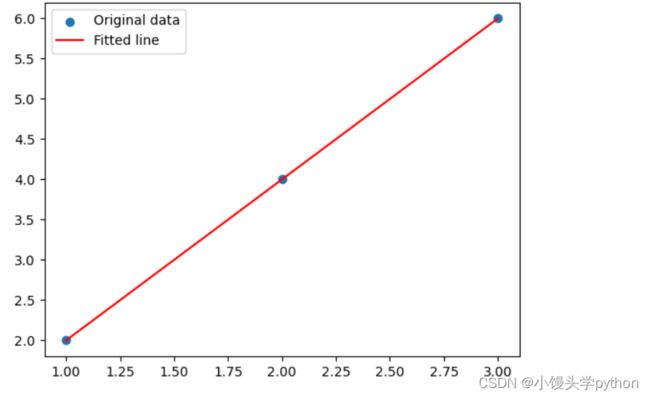
predicted = model(x_data).detach().numpy()
plt.scatter(x_data, y_data, label='Original data')
plt.plot(x_data, predicted, label='Fitted line', color='r')
plt.legend()
plt.show()
总结
在本篇博客中,我们使用PyTorch实现了一个简单的线性回归模型,并使用随机生成的数据对其进行了训练和可视化。线性回归是一个入门级的机器学习模型,但它为理解模型训练和预测的基本概念提供了一个很好的起点。
挑战与创造都是很痛苦的,但是很充实。