一文概览时间序列

原创：张春阳

用这些模型扩展你的时间序列库

Regularizing, Bagging, Stacking

时间序列数据通常有四个组成部分：

• Autoregression
• Seasonality
• Trend
• Residual

如果能够预测这些成分，你几乎可以预测任何时间序列。听起来很简单，对吧？

但是不完全是这样。关于指定模型的最佳方法有很多不好确定的地方，为了能够更好地解释这些元素，过去几年中已经发布了许多研究来寻找最佳方法，最先进的模型，其中以递归和其他神经网络模型占据了中心地位。除此之外，许多系列还有其他需要考虑的影响，比如假期和规律性的休息。

总而言之，预测任何给定的序列通常不像使用线性回归那么容易。非线性估计和集成方法可以与线性方法相结合，以找到任何序列的最佳方法。在这篇文章中，我从 Scitkit 学习库中拿出了这些模型的示例，以及如何利用它们来最大限度地提高准确性。这些方法应用于每日访客数据集，可在 Kaggle 或 RetressionIt 上找到 2000 多个观测值。

这篇博文的结构相当重复，每个应用模型都有相同的图表和评估指标。如果您已经熟悉了 Scikit 中的机器学习模型和 API，比如 MLR、XGBoost 等，那么可以直接跳到 Bagging 和 Stacking 部分来看它们之间的差异性的对比。你可以在 GitHub 上找到完整的笔记本。

准备模型

所有模型都使用 scalecast 软件包运行，该软件包包含结果，并围绕时间序列数据包装 Scikit learn 和其他模型。默认情况下，其所有预测都使用动态多步预测，与平均一步预测相比，它在整个预测期内返回更合理的准确性/误差指标。

pip install scalecast

我们将使用60天的预测期，也将使用60天集来验证每个模型并调整其超参数。所有模型将在20%的原始数据上进行测试：

f=Forecaster(y=data['First.Time.Visits'],current_dates=data['Date'])
f.generate_future_dates(60)
f.set_test_length(.2)
f.set_validation_length(60)

从 EDA（此处未显示）来看，过去4周内似乎存在自相关，前7个因变量滞后可能是显著的。

f.add_ar_terms(7) # 7 auto-regressive terms
f.add_AR_terms((4,7)) # 4 seasonal terms spaced 7 apart

对于该数据集，必须考虑几个季节性因素，包括每日、每周、每月和季度波动。

f.add_seasonal_regressors(
    'month',
    'quarter',
    'week',
    'dayofyear',
    raw=False,
    sincos=True
) # fourier transformation
f.add_seasonal_regressors(
    'dayofweek',
    'is_leap_year',
    'week',
    raw=False,
    dummy=True,
    drop_first=True
) # dummy vars

最后，我们可以通过添加年份变量来模拟该系列的趋势：

f.add_seasonal_regressors('year')

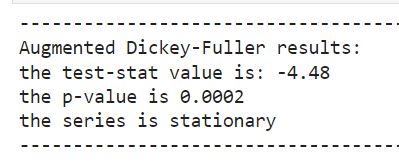
对于所有这些模型，通常需要向它们提供平稳的时间序列数据。我们可以通过增强的Dickey Fuller测试确认该数据是平稳的：

MLR

我们将从简单开始，尝试应用多元线性回归（MLR）。该模型快速、简单，无需调整超参数。它通常具有极高的准确性，即使使用更先进的方法也很难击败它。

它假设模型中的所有组件可以以线性方式组合，以预测最终输出：

上图公式中，j 是增加的回归数（在我们的例子中，AR、季节和趋势分量），α 是相应的系数。在我们的代码中，调用此函数如下所示：

f.set_estimator('mlr')
f.manual_forecast()

值得注意的是，时间序列的线性方法更常见的模型是 ARIMA，它也使用序列的误差作为回归。MLR假设序列的误差是不相关的，这在时间序列中是虚假的。也就是说，在我们的分析中，使用 MLR 获得了13%的测试集平均绝对百分比误差和76%的 R2。让我们看看是否可以通过增加复杂性来克服这一点。

Lasso

接下来回顾的三个模型，Lasso、Ridge 和 ElasticNet，都使用 MLR 的相同基