基于TensorFlow分析MNIST数据集

目录

MNIST数据集分析及预处理

CPU/GPU的选择

比较分析

具体操作

建立模型

编译模型

训练模型

评估模型

保存模型

结果可视化

使用模型进行预测

AutoEncoder自编码器

普通自编码器

卷积自编码器

MNIST数据集分析及预处理

可以参考：

MNIST数据集简单介绍_THE WHY的博客-CSDN博客

CPU/GPU的选择

比较分析

CPU：中央处理器（Central Processing Unit），可以进行复杂度较高的通用计算，但计算量较小；

GPU：图形处理器（Graphics Processing Unit），可以进行复杂度较低的简单运算，但计算量较大

基于二者以上的特性，我们可以看出，要对MNIST进行分析，主要进行的是图形类矩阵运算，计算量较大，但不涉及复杂的运算，因此选用GPU较为合适；

具体操作

在选用GPU之前，首先我们需要确定自己的电脑上是否有GPU，而且为了避免版本不支持，最好安装使用最新的 TensorFlow GPU 版本，我个人使用的是2.11.0版本

代码实现如下：
查看是否有可用的GPU：

print(tf.test.is_gpu_available())

如果返回值为False，则说明没有可用的GPU

也可以打印GPU列表来进行查看：

pring(tf.config.experimental.list_physical_devices('GPU'))

如果没有可用的GPU，我们可以选择安装GPU或者使用CPU

使用CPU无需进行额外的配置，默认就是使用CPU，当然也可以查看当前可用的CPU：

pring(tf.config.experimental.list_physical_devices('CPU'))

如果有可用的GPU，我们可以从中选择合适的进行使用

gpu = tf.config.experimental.list_physical_devices('GPU')
tf.config.experimental.set_memory_growth(gpu[0],True) #具体选用哪个视情况而定

建立模型

通过tf.keras.models.Sequential()方法建立模型

Sequential是一个容器，可以将线性堆栈的层加载到模型中，从而创建由输入层到输出层的网络结构；

# 建立模型
model = tf.keras.Sequential()
# 通过add方法向模型中加载网络层(layer)
model.add(tf.keras.layers.Flatten(input_shape=(28,28))) # 每个样本有28*28个像素点，通过拉直层进行输入
model.add(tf.keras.layers.Dense(128,activation='relu')) # 隐含层，设置128个结点，激活函数使用Relu
model.add(tf.keras.layers.Dense(10,activation='softmax')) # 输出层，设置10个结点（数字0-9），激活函数使用softmax归一化

用到的layer有Flatten和Dense

Flatten用于处理输入，对输入的张量进行扁平化处理，通过input_shape=(28,28)可以看出，我们的输入规模是28*28的一个二维数组，通过Flatten层可以将其转化为一维数组，从而将这些数据有效地传递到模型的每一个神经元中

Dense：全连接层，我们的隐含层和输出层全部选用Dense结构，参数设置如下：

Dense(神经元个数，activation = "激活函数“，kernel_regularizer = "正则化方式）

激活函数可选：relu 、softmax、 sigmoid、 tanh等

正则化方式可选：tf.keras.regularizers.l1() 、tf.keras.regularizers.l2()等

• 在隐含层中，设置128个结点，激活函数使用Relu函数；

• • sigmod函数：

    

  • relu函数：

    

  • 相比之下，relu函数简化了计算过程，消除了指数函数对于梯度下降的影响，可以减少计算成本，因此我们选用relu函数

• 在输出层中，设置10个结点（输出数字0-9），激活函数使用softmax函数，进行归一化处理；

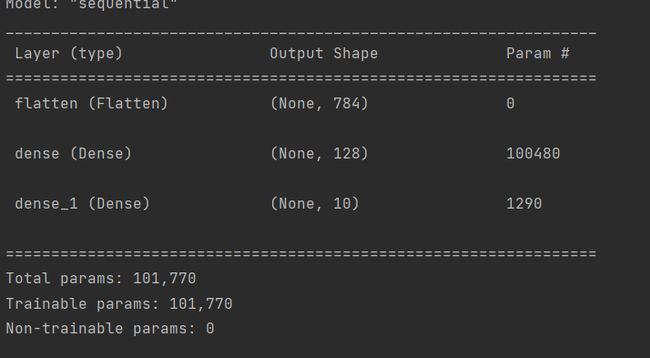
在模型建立之后，我们可以打印模型相关信息：

print(model.summary())

输出结果如下：

Layer (type)：网络层的名称（类型），名称可以通过tf.keras.layers.Dense()中的name属性指定

Output Shape：每一层的输出形状

Param：全连接层神经网络每层神经元权重的个数；计算公式：（input_shape+1）* 神经元个数

• 例如dense_1层，input_shape=128，神经元个数为10，（128+1）*10=1290

编译模型

通过compile方法进行模型的编译：

# 优化器:选用adam优化器，学习率设置为0.1
optimizer = tf.keras.optimizers.Adam(lr=0.1)
# 损失函数:选用交叉熵损失函数 ‘from_logits=False’ 表示将输出转为概率分布的形式
loss_fn = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False)
model.compile(optimizer=optimizer,loss=loss_fn,metrics=['accuracy'])

方法有三个参数：

1.optimizer：优化器，可以是函数形式，也可以是字符串形式；选用adam优化器：

optimizer="adam"或者optimizer=tf.keras.optimizers.Adam()

选用函数形式可以配置学习率：tf.keras.optimizers.Adam(lr=)，默认的学习率是0.001

具体信息及其他优化器参考：tf.keras.optimizers.Adam  |  TensorFlow v2.12.0

2.loss：损失函数，可以是函数形式，也可以是字符串形式；选用稀疏分类交叉熵损失函数：

loss="sparse_categorical_crossentropy"或者loss=tf.keras.losses.SparseCatagoricalCrossentropy(from_logits = False)

其他常用的损失函数还有MSE，与交叉熵损失函数对比如下：

MSE：

Cross-entropy：

由于交叉熵损失函数梯度下降时不容易在局部最优解"stuck"，因此优先选用；

具体信息及其他损失函数参考：tf.keras.losses.SparseCategoricalCrossentropy  |  TensorFlow v2.12.0

3.metrics：准确率评测标准，常用选项：'accuracy',sparse_accuracy,sparse_categorical_accuracy

具体信息参考：tf.keras.metrics.Accuracy  |  TensorFlow v2.12.0

训练模型

通过fit方法来进行模型的训练：

history = model.fit(x_train,y_train,batch_size=128,epochs=10,validation_split=0.1,verbose=2)

参数解析：

fit(x=None, y=None, batch_size=None, epochs=1, verbose=1,validation_split=0.0)

x，y：输入输出，必填项

batch_size：每次梯度更新的样本数，默认值是32

epochs：迭代次数

verbose：日志打印的格式：0:不输出日志信息；1:显示进度条；2:每迭代一次输出一行记录

validation_split：分割训练数据集的一部分作为验证数据，剩余的作为训练数据；

返回内容：

fit方法的返回值是一个History对象，包括数据集的损失和训练的准确率

loss = history.history['loss']
val_loss = history.history['val_loss']
accuracy = history.history['accuracy']
val_accuracy = history.history['val_accuracy']
print("训练集损失:",loss)
print("测试集损失:",val_loss)
print("训练集准确率:",accuracy)
print("测试集准确率:",val_accuracy)
# 注意，key的名称与选择的损失函数和准确率评测标准有关

打印结果如下：

可以看到每一次迭代的相关参数都打印了出来；

详细信息参考：tf.keras.Model  |  TensorFlow v2.12.0

评估模型

通过evaluate来评估模型：

model.evaluate(x_test,y_test,verbose=2)

参数解析：

model.evaluate(x,y,batch_size,verbose)

x，y：测试数据集，测试数据集的标签

batch_size：每次评估计算使用的样本多少

verbose：日志打印的格式：0:不输出日志信息；1:显示进度条；2:每迭代一次输出一行记录

详细信息参考：tf.keras.Model  |  TensorFlow v2.12.0

保存模型

参数解析：

model.save(存储路径)：将模型保存到相应的路径下

model.save(模型名称)：不指定路径，则默认保存到当前的工作路径下

由此我们可以将整个训练好的模型保存下来，使用的时候直接加载即可：

model = tf.keras.models.load_model(模型路径)

该模型可以直接用于model.predict

详细信息参考：训练检查点  |  TensorFlow Core

结果可视化

结果可视化需要用matplotlib.pyplot来进行绘图

官方文档：matplotlib — Matplotlib 3.7.1 documentation

1.plt.figure：自定义画布相关属性

plt.figure(num='first',figsize=(10,3),dpi=75, facecolor='#FFFFFF', edgecolor='#0000FF')

num：图像的编号；figsize：画布的大小；dpi：每英寸的像素；facecolor：画布颜色；edgecolor：画布边缘的颜色

文档：matplotlib.figure — Matplotlib 3.7.1 documentation

2.plt.subplot(nrows, ncols, index)：用于一次性绘制多个子图

图表的整个绘图区域被分成 nrows 行和 ncols 列

按照从左到右，从上到下的规则对子图进行编号，index指定了要绘制的子图在整个绘表区域的位置

文档：matplotlib.pyplot.subplot — Matplotlib 3.7.1 documentation

3.plt.plot：绘制折线图

plt.plot(x,y,color='b',label='标签名称')

x：x轴数据；y：y轴数据；color：标签的颜色（常用：b-蓝色，r-红色）

如果只填入一组数据，则x轴的缺省值填充为[0,1,2,3,4.......]，即y[]的长度

文档：matplotlib.pyplot.plot — Matplotlib 3.7.1 documentation

4.plt.xlabel() plt.ylabel()：x，y轴的单位名称

5.plt.legend()：自动检测图例中应当显示的元素并使其显示出来

6.plt.title()：设置标题

根据以上常用的绘图API，我们可以绘制loss和accuracy的变化曲线；

plt.figure(figsize=(10,3))
plt.plot(loss,color='b',label='train')
plt.plot(val_loss,color='r',label='test')
plt.ylabel('loss')
plt.legend()

plt.figure(figsize=(10,3))
plt.plot(accuracy,color='b',label='train')
plt.plot(val_accuracy,color='r',label='test')
plt.ylabel('accuracy')
plt.legend()

使用模型进行预测

①从测试数据集中随机选取一个图像：

id = np.random.randint(1,10000)

②通过tf.reshape进行重构，使其符合模型的输入格式；

num = tf.reshape(x_test[id],(1,28,28)) 

③通过model.predict进行预测：

model.predict(num)

④获取预测结果

res = np.argmax(model.predict(num))

从预测得到的结果（格式如下）中找到最大值，作为预测结果

---

2023.4.10更新： 

AutoEncoder自编码器

普通自编码器

自编码器是一种无监督的数据维度压缩和数据特征表达方法，由两部分构成：

编码器（encoder）:将输入压缩成潜在空间表征

解码器（decoder）:重构来自潜在空间表征的输入

简单来说，自编码器是一种试图让输出和输入相同的一种神经网络，通过设置潜在空间表征的维度小于输入数据的维度，使得自编码器不完整，从而强迫自编码器学习输入数据的显著特征，从而更好地从数据中抽取有用的信息，在重构来自潜在空间表征的输入时准确率也就更高；

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf

from keras import layers
from keras.models import Model

# 加载数据
mnist = tf.keras.datasets.mnist
(x_train, _), (x_test, _) = mnist.load_data()

# 获取训练集和测试集
x_train, x_test = x_train / 255.0, x_test / 255.0

# 选取10%的训练数据集
x_train = x_train[0:6000]

latent_dim = 64 # 控制编码器的压缩程度（隐含层的结点数量）

class Autoencoder(Model): # 继承Model类，自定义自编码器模型
  def __init__(self, latent_dim):
    super(Autoencoder, self).__init__() # 自编码器的初始化
    self.latent_dim = latent_dim
    # 编码器，将原始图像压缩成64维的隐向量，相当于是隐含层
    self.encoder = tf.keras.Sequential([
      layers.Flatten(),
      layers.Dense(latent_dim, activation='relu'),
    ])
    # 解码器，从隐空间中重构图像
    self.decoder = tf.keras.Sequential([
      layers.Dense(784, activation='sigmoid'),
      layers.Reshape((28, 28))
    ])

  def call(self, x):
    encoded = self.encoder(x) # 先编码
    decoded = self.decoder(encoded) # 然后解码
    return decoded # 返回解码后的图像

autoencoder = Autoencoder(latent_dim) # 创建自编码器

# 由于Autoencoder继承了Model类，因此创建的自编码器也就相当于一个自定义模型，可以使用model的方法对模型进行编译，训练
# 编译模型:使用adam优化器，交叉熵损失函数
autoencoder.compile(optimizer='adam', loss='categorical_crossentropy')
# 训练模型
autoencoder.fit(x_train, x_train,
                epochs=10,
                shuffle=True,
                validation_data=(x_test, x_test))
# 保存训练的模型
autoencoder.save_weights("AEtest.h5")

# 模型训练完成，输入测试集中的数据进行预测
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()

n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
  # 随机选取测试集中的一张图像
  num = np.random.randint(1, 10000)

  # 展示初始的图像
  ax = plt.subplot(2, n, i + 1)
  plt.imshow(x_test[num])
  plt.title("original")
  plt.gray()
  ax.get_xaxis().set_visible(False)
  ax.get_yaxis().set_visible(False)

  # 展示经过自编码器处理之后的图像
  ax = plt.subplot(2, n, i + 1 + n)
  plt.imshow(decoded_imgs[num])
  plt.title("reconstructed")
  plt.gray()
  ax.get_xaxis().set_visible(False)
  ax.get_yaxis().set_visible(False)
plt.show()

结果如下：

上层是输入的测试集，下层是通过自编码器编码、解码之后得到的图像；

以上测试使用的是MNIST数据集，使用了其中10%的数据；代码实现修改自官网的示例：

Intro to Autoencoders  |  TensorFlow Core

通过上面的结果我们可以看到，解码器重构的效果只能说是一般，通过模型训练时打印的信息也能看出，loss和val_loss都比较大：

而这种现象在我们只采用1%的数据集时更加明显，由于训练样本的不足，使得自编码器不能很好地学习数据的特征：

如上图所示，出现了很抽象的结果；

于是我将训练的迭代次数设置增加到了100：

但发现测试值的损失（val_loss）会出现上升的情况，于是由尝试了迭代200次的情况，可以看到loss的下降非常有限：

测试的结果也不尽如人意：

这说明普通自编码器不擅长从小规模的数据集中提取有效的特征；

卷积自编码器

为了解决这个问题，我又尝试了卷积自编码器：

所谓卷积自编码器，简单来说就是用卷积神经网络代替了普通自编码器中的全连接神经网络来进行特征提取和重构；

代码实现如下：（也是根据官网的代码进行了修改）

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf

from keras import layers,losses
from keras.models import Model

# 加载数据
mnist = tf.keras.datasets.mnist
(x_train, _), (x_test, _) = mnist.load_data()

# 获取训练集和测试集
x_train, x_test = x_train / 255.0, x_test / 255.0

# 选取10%的训练数据集
x_train = x_train[0:600]

latent_dim = 64 # 控制编码器的压缩程度（隐含层的结点数量）

class Denoise(Model):
  def __init__(self):
    super(Denoise, self).__init__()
    self.encoder = tf.keras.Sequential([
      layers.Input(shape=(28, 28, 1)), # shape=(28,28,1)分表表示RGB图像的高，宽和通道数（由于MNIST数据集是单色的，所以通道数为1
      # 输入的每一个通道都要与每一个卷积核进行卷积运算，生成特征图
      # 每个通道都可以看做是原始图像的一个抽象，堆的越多，神经网络汇总每一层的信息就越多，原始图像的损失就越少
      # 而在自编码器中，对输入的象征进行降采样以提供较小维度潜在表示，并强制自编码器学习象征的压缩版本
      # 这里输入1个通道，设置16个卷积核，进行卷积运算后生成16个特征图，从而输出通道数就是16
      layers.Conv2D(16, (3, 3), activation='relu', padding='same', strides=2),
      # 这里输入16个通道，设置8个卷积核，进行卷积运算后生成8个特征图，从而输出通道数就是8
      layers.Conv2D(8, (3, 3), activation='relu', padding='same', strides=2)])

    self.decoder = tf.keras.Sequential([
      # 卷积的逆操作
      layers.Conv2DTranspose(8, kernel_size=3, strides=2, activation='relu', padding='same'),
      layers.Conv2DTranspose(16, kernel_size=3, strides=2, activation='relu', padding='same'),
      # 设置1个通道，生成的特征图就是经过自编码器编码解码处理后的图像
      layers.Conv2D(1, kernel_size=(3, 3), activation='sigmoid', padding='same')])

  def call(self, x):
    encoded = self.encoder(x)
    decoded = self.decoder(encoded)
    return decoded

autoencoder = Denoise()


autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())# 训练模型

autoencoder.fit(x_train, x_train,
                epochs=10,
                shuffle=True,
                validation_data=(x_test, x_test))
# 保存训练的模型
# autoencoder.save_weights("AEtest.h5")

# 模型训练完成，输入测试集中的数据进行预测
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()

n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
  # 随机选取测试集中的一张图像
  num = np.random.randint(1, 10000)

  # 展示初始的图像
  ax = plt.subplot(2, n, i + 1)
  plt.imshow(x_test[num])
  plt.title("original")
  plt.gray()
  ax.get_xaxis().set_visible(False)
  ax.get_yaxis().set_visible(False)

  # 展示经过自编码器处理之后的图像
  ax = plt.subplot(2, n, i + 1 + n)
  plt.imshow(decoded_imgs[num])
  plt.title("reconstructed")
  plt.gray()
  ax.get_xaxis().set_visible(False)
  ax.get_yaxis().set_visible(False)
plt.show()

第一次测试我设置了两层卷积网络，卷积核分别是16,8：

迭代10次进行训练，训练过程和测试结果如下

由于卷积网络的卷积核数对应的就是图像的通道数，而每个通道都可以看做是原始图像的一个抽象，因此通道越多，神经网络获得的信息就越多，原始图像的损失就越少，所以我又进行了以下测试：

设置两层卷积网络，卷积核分别是32,16：

迭代10次进行训练，训练过程和测试结果如下

可以看到，损失下降的效果和图像拟合的效果都比较不错

最后总结一下CNN自编码器的优缺点：

CNN自编码器是一种利用卷积神经网络进行特征提取和重构的自编码器，其优缺点如下：

优点：

可以提取图像的局部特征：卷积神经网络具有良好的局部感知能力，可以提取图像的局部特征，因此CNN自编码器可以更好地保留图像的局部结构。

可以自适应地学习特征：CNN自编码器可以自适应地学习图像的特征，无需手动设计特征提取器，因此可以更好地适应不同的数据集和任务。

可以用于图像降噪和去除伪影：CNN自编码器可以学习到图像的低维表示，可以用于图像降噪和去除伪影等任务。

缺点：

训练时间较长：由于CNN自编码器需要学习大量的参数，因此训练时间较长，需要较大的计算资源和时间。

容易过拟合：由于CNN自编码器具有较强的学习能力，容易在训练集上过拟合，导致在测试集上表现不佳。

对于大规模图像处理效率较低：由于CNN自编码器需要对整张图像进行卷积操作，因此对于大规模图像的处理效率较低。

由上也可以看出，对于MNIST数据集进行训练，使用CNN自编码器的效果会更好一些，尤其是在训练数据样本较少的情况下；CNN自编码器可以更好地处理图像数据，因为它们可以利用卷积层来提取图像中的空间特征。这些卷积层可以捕捉到输入图像中的局部模式和结构，从而更好地重建图像。此外，CNN自编码器还可以使用池化层来减小图像的空间尺寸，从而减少模型的参数数量，提高训练效率；

暂时就学习了这些内容，未完待续；

（如果文章中有错误的地方，欢迎大家指正！作者是刚入门的小白，难免会有理解不到位的地方~）