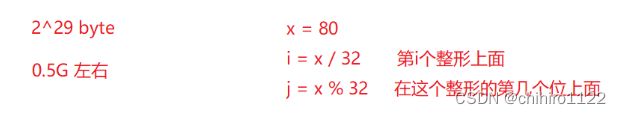C++ - 位图 - bitset 容器介绍
前言
之前的两篇博客已经完成 闭散列的开放地址法的哈希表 和 哈希桶基本实现,和对 unordered_set 和 unordered_map 的封装 :
C++ - 封装 unordered_set 和 unordered_map - 哈希桶的迭代器实现_chihiro1122的博客-CSDN博客C++ - 开散列的拉链法(哈希桶) 介绍 和 实现-CSDN博客
C++ - 开放地址法的哈希介绍 - 哈希表的仿函数例子_chihiro1122的博客-CSDN博客
但是,在哈希桶当中有一个很致命的问题,当一个 桶当中的数据过多的时候,比如,现在有 N 个数据,但是有 n-1 个数据都在一个桶当中,这种情况是完全可能发生 的,那么这个哈希桶就退变为一个链表了,搜索的时间复杂度不再是 O(log N)而是 O(N)了。
上述这种情况,我们之前也说过,当扩容的时候,就会重新按照新的哈希函数来排列其中的数据,那么就会对长的桶进行拆解,一般来说上述这种情况是很难发生的。
但是,极端场景下就会发生。
为了防止上述情况的发生,就演化出了两种方法来处理。
在JAVA当中就会这种极端场景进行了细致处理:
在JAVA 当中,如果某一个桶当中超过了某一个个数,比如这个个数是 8个,那么当这个桶当中的数据超过 8 个,就会把从这个结点开始的后面的结点的都转化为红黑树。如果后续删除结点,删除到 这个桶当中的数据小于8 了,那么就又转化为 桶也就是类似单链表的结构。
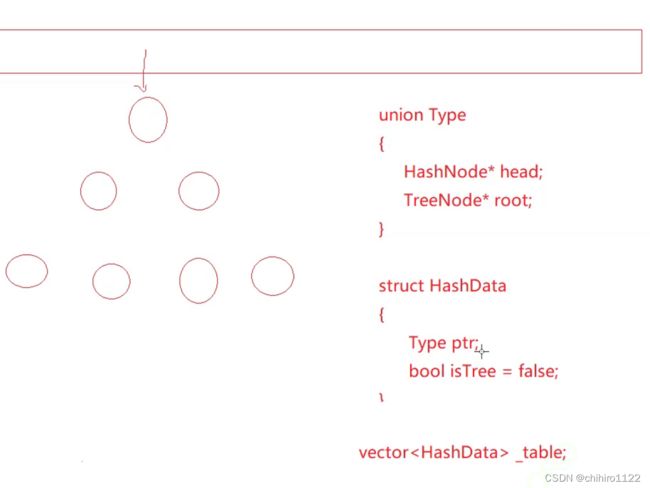
如果在 C/C++ 当中要实现这种方式,结点有类似这种写法:
在 指针数组 vector 当中,存储一个结构体 HashDate,这个结构体当中有两个成员,一个是 是否是 树的 bool值,一个是 指针的联合体,这个联合体当中有两个指针,这个联合体的大小只有 4 个字节,就存储一个指针,如果 isTree 是 true,这个联合体就存储 root指针;如果是 false 就存储 head。
当然,按照我们上述说的逻辑,这里不用 bool 值来判断,用的是 这个桶的结点个数来判断:
size_t bucket_size; 如果这个 bucket_size 大于8,那么就存储 root ,反之了。
那么上述这种哈希桶加红黑树的结构是完全无惧冲突的,因为就算一个桶当中存储了 100w 个数据,那么在进化成红黑树之后,查找也就是 20 次。
在哈希当中有人提出了,如果哈希表的长度按照素数的方式进行扩容的话,也就是扩容按照素数的长度进行扩容,这样可以防止一些冲突。
size_t GetNextPrime(size_t prime)
{
const int PRIMECOUNT = 28;
static const size_t primeList[PRIMECOUNT] =
{
53ul, 97ul, 193ul, 389ul, 769ul,
1543ul, 3079ul, 6151ul, 12289ul, 24593ul,
49157ul, 98317ul, 196613ul, 393241ul, 786433ul,
1572869ul, 3145739ul, 6291469ul, 12582917ul,
25165843ul,
50331653ul, 100663319ul, 201326611ul, 402653189ul,
805306457ul,
1610612741ul, 3221225473ul, 4294967291ul
};
size_t i = 0;
for (; i < PRIMECOUNT; ++i)
{
if (primeList[i] > prime)
return primeList[i];
}
return primeList[i];
}如上,就按照上述数组当中的素数来进行扩容。
这种扩容的方式,虽然在 C++ 当中使用了,但是在 JAVA 当中没有使用。
但是也不是所以的 C++ 编译器都是使用素数的方式扩容,在 VS2013 和 VS2019 当中是使用 8倍 和 2倍结合来扩容的,而且 g++ 当中是,c++11 当中是按照 原本空间 2倍左右的素数 来扩容的。
g++ 当中实现就和上述类似了,搞一个素数的表,然后扩容先 *2,然后在素数表当中找到 *2 后大小左右素数。
位图
我们先来看一个问题:
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在
这40亿个数中。
首先我们来看,假设 一个数的类型是 int 类型的话,那么存储这个 40 亿的数据需要多少个G。
假设是 40 亿个整数的话,需要 160亿 Byte,那么 160亿 字节 换算成 G 大概是 16 G 左右,试问,我们今天使用的电脑有多少是 可以自己使用 16G 的,就算我们使用的笔记本是 16 G 的,我们也不能整整用上 16G,因为 操作系统的文件什么也需要占用空间。
而且,就算可以使用 32G 内存的机器,如果我们把数据量提升到 80亿 呢? 100亿 呢?所以不能从根本上解决问题。
这也就导致了我们之前学过的插入方法比如:set容器,排序+二分查找,哈希表等等都不行了,set 和 哈希表就更不用说了,set 和 哈希表的实现就要比int整数普通的存储要多消耗空间。
所以,此时就有了位图的出现。
位图的实现逻辑
我们想到这个题目只是要判断一个 数是否存在,那么我们其实没有必要存储这个数,只需要存储这个数是否存在就行了。
那么只需要存储一个数是否存在,只需要 0 和 1 就可以表示,也就是说,在计算机当中最小的存储单位-比特位,一个位就可以表示 一个 数是否存在了。那么,按照上述的说法,在 32 位机器下,一个 int 类型是 4 个字节,也就是 32 位,如果我们把上述方式替换到用位存储的话,我们可以整整节省 32 倍的空间。理论上,40 亿个整形数据,我们只需要 500M 就可以存储是否存在了。
但是在 C/C++ 当中不能按照 比特位的大小去开值,没有这个大小的类型,最小 char 类型都有一个字节。
所以,其实我们直接按照 int 的大小去开辟空间(其实按照 char 类型去开辟空间也是一样的),然后通过位运算操作符,修改 一个 int 当中的 32个 比特位,这样来实现 修改 某一个 比特位 操作。
所以,我们就利用一个 vector
如下图,是vector 当中,图中标出的下标是 比特位的下标,在 vector 当中的每一个 小 长方形代表的是 一个 int 类型的数据:
那么想要修改某一个比特位,我们就要先取到这个比特位:
一个 int 类型是 32 位,那么 按照上述的说法,比特位的下标就代表 这个比特位存储是哪一个 数是否存在的值。
所以,我们要想找到这个目标数存储在vector 数组当中的那亿比特位,那么就得先拿 目标数 / 32
这个计算的结果表示,这个数是在vector 当中的那一个 int 类型的数据当中的。
然后在哪 目标数 % 32 ,这个的计算结果是 这个目标数是在 上述 计算的 int 类型数据当中的 哪一个 比特位。
假设,我们现在想把 第10位的比特位修改成 1 ,那么我们可以按照上述的方式找到 这个 第10 位比特位,但是我们要如何进行修改呢?
我们可以利用 " | " 这个操作符,这个操作符是 :有1 为 1。
如果我们想把 某一位 的 比特位 修改为 1 ,那么我们只需要创建一个数据 ,这个数据是:
00000 ····· 1 ······ 00000
也就是,除了 要修改的比特位 为 1 ,其他位都为 0,那么我们把这个数 和 我们想要修改的比特位 存储 的某一个 int 类型的数据 做 " | " 。所得到的结果就是 我们想要的修改之后的结果。
那么,知道了如何修改,那我们如果 创建这样一个数据呢?
我们发现, int 类型 数据 1 的 二进制是这样写的 00000······· 0001 ,那么,我们把 1 左移 到 我们想要的比特位上不就好了吗?至于要存储多少位,上述 j 变量已经计算出来了,也就是那 目标数据 % 32 就可以得到在哪一位。
现在可能就有人问了,在计算机当中的数据存储,大多数按照都不是 下端机器的存储方式吗?
所谓下端机器存储方式是按照 低地址存储低位的数据,比如,要存储 整形 1 ,那么我们理解的存储 顺序是 00 00 00 01 ,这样的结构,但是在小端机器当中存储的顺序是 01 00 00 00 ,这样的顺序,那么这也就导致了, 1 这个数据在 vector 当中存储的结构,和 比特位的顺序应该是这样的了:
假设,按照上述的逻辑 ,用 整形 1 来左移来创建一个 数,那么 整形 1 当中 二进制的1 就在上述 的 0 下标这个位置,假设我们现在要左移到 10 下标的位置,那么左移到 7 不就结束了吗,怎么左移到 15 - 8 这个区间当中呢?
其实,上述的 大小端只是数据在计算机当中的存储方式,我们在使用这个数据的时候根本就不用关心这个数据的存储方式是大端还是小端,我们在使用的逻辑就是 按照 00 00 00 01 这样的顺序来操作的,关于大端和小端是在底层自己给我们处理,所以我们不用担心。
如果我们想要把 某一个 比特位 修改为 0的话,就要使用 " & " 这个操作符,这个操作符是 有0 则 0 ,那么我们想要把 某一个位 修改为 0 ,不懂其他位的话,就要创建一个 1111····· 0 ······ 1111 这样第一个数,和 这个位 所在 int 数据 进行 " & " 运算,运算出的结果就是 我们想要的修改之后的结果。
那么,要想创建一个 1111····· 0 ······ 1111 的数的话,我们发现 ,在上述 把 某一比特位 修改为 1时候,我们创建的 数,刚好和这个数 是 取反的逻辑,所以,我们只需要 创建一个 上面的数,然后 使用 "~" 按位取反就行了:
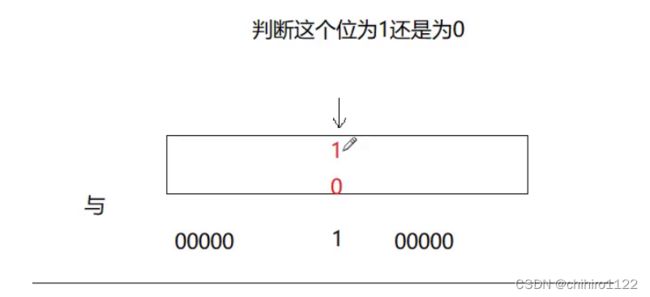
判断某一个位 是 1 还是 0 ,也就是判断这个数在不在。
我们同样利用 " & " 的 特性,1 跟 0 & 是 0, 1 跟 1 & 还是 1 ,所以,我们创建一个 0000·····1······0000 这个数,来做 & 运算,就可以取出 我们像查看的 比特位的值了,也就判断某一个数是否存在了。
上述直接返回从 比特位上取出的 0 或者 1 ,0就是 false,非0 就是 true,刚好满足。
构造函数
位图的空间存储,这里我们使用静态的方式进行开辟空间,不进行扩容操作,使用 确定类型的模版参数,这样在外部就可以传入大小-N,那么我们在构造函数当中就可以对 vector 开辟一个 N 的大小的空间:
bitset()
{
_a.resize(N / 32 + 1);
}
完整代码
#pragma once
#include
namespace bit
{
template
class bitset
{
public:
bitset()
{
_a.resize(N / 32 + 1);
}
// x映射的那个标记成1
void set(size_t x)
{
size_t i = x / 32;
size_t j = x % 32;
_a[i] |= (1 << j);
}
// x映射的那个标记成0
void reset(size_t x)
{
size_t i = x / 32;
size_t j = x % 32;
_a[i] &= (~(1 << j));
}
bool test(size_t x)
{
size_t i = x / 32;
size_t j = x % 32;
return _a[i] & (1 << j);
}
private:
vector _a;
}; 库当中的位图(bitset容器介绍)
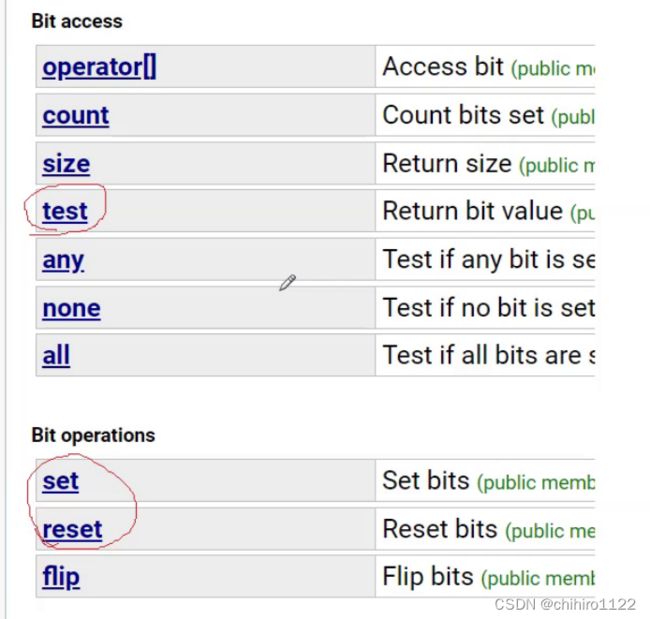
我们不需要手撕一个位图,库当中就实现了位图。
其中的 set 和 reset , test 函数也是和我们上述实现差不多,用法也是一样的。、
其中的 operator[]()是可读可写的函数,可以利用这个函数把 某一个 比特位修改为 0 或者 1:
std::bitset<4> foo;
foo[1]=1; // 0010
foo[2]=foo[1]; // 0110
std::cout << "foo: " << foo << '\n';
位图的应用
我们在开头就说过了一个 40亿数据的例题,接下来我们继续来看一些例题:
1. 给定100亿个整数,设计算法找到只出现一次的整数?
我们可以用两个比特位来表示 一个 整数出现的此处,首先,两个位 能够表示 四种情况:00 01 10 11; 00 就是出现 0 次,那么当插入这个数据之后,就会依次 增加1 ,到 01 和 10,当到达 10 的时候就表示出现了两次了,那么以后再出现就不增加了。之后只需要遍历 整个 位,就可以知道那些整数出现了一次了。
当然上述不是最好的方式,更好的方式是 开两个位图,这样把 两个位图 对应位置上比特位的值 组合起来就和上述的一样了。
解题思路就是,创建一个新的 位图,这个位图当中有两个 我们之前实现的 位图成员,在这个新的位图类当中,我们只需要实现set()插入函数,和 一个 判断 某个数是不是只出现一次的 函数
在set()函数当中,我们不需要对 00 或者 01 这样的++,因为只有两种方式的增加,所以我们直接判断,写死了修改就行了。
代码实现:
template
class twobitset
{
public:
void set(size_t x)
{
// 00 -> 01
if (!_bs1.test(x) && !_bs2.test(x))
{
_bs2.set(x);
} // 01 -> 10
else if (!_bs1.test(x) && _bs2.test(x))
{
_bs1.set(x);
_bs2.reset(x);
}
// 本身10代表出现2次及以上,就不变了
}
bool is_once(size_t x)
{
return !_bs1.test(x) && _bs2.test(x);
}
private:
bitset _bs1;
bitset _bs2;
};
} 2.给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
可以创建两个位图,一个位图映射一个文件当中的内容,不需要按照上述的方式去计算个数,只需要用一个位存储是否在就行了,而后序重复数据也只要改为1 就行了,这样就相当于是做到了去重的效果。
两个位图取 与 得出的结果,找到 1 说明这个数就是有交集的。
int a1[] = {1,2,3,3,4,4,4,4,4,2,3,6,3,1,5,5,8,9 };
int a2[] = {8,4,8,4,1,1,1,1};
bit::bitset<10> bs1;
bit::bitset<10> bs2;
// 去重
for (auto e : a1)
{
bs1.set(e);
}
// 去重
for (auto e : a2)
{
bs2.set(e);
}
for (int i = 0; i < 10; i++)
{
if (bs1.test(i) && bs2.test(i))
{
cout << i << " ";
}
}
cout << endl; 3.位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整
数
这个问题和问题一个方式解决,使用两个位图, 11 就代表是出现两次。