B树与B+树
B树
二叉树是二分树,多分树是二叉树的推广。多分树主要适用于静态的索引数据文件,在插入和删除的时候需要把插入位置之后的每个记录都要向后移动,从而导致增加新的索引项和索引页块,需要对外存上的页块进行大量的调整。因此对于经常需要插入和删除的动态索引顺序文件,使用多分树并不合适,需要采用动态索引结构,即B树和B+树。
B树是一种自平衡树,是AVL树的一般化,它维护有序数据并允许以对数时间进行搜索,顺序访问,插入和删除。与AVL树不同的是,B树非常适合读取和写入相对较大的数据块(如光盘)的存储系统。它通常用于数据库和文件系统。
1 B树的定义
一颗m阶的B树满足如下条件:
每个节点最多只有m个子节点。
除根节点外,每个非叶子节点具有至少有 m/2(向下取整)个子节点。
非叶子节点的根节点至少有两个子节点。
有k颗子树的非叶节点有k-1个键,键按照递增顺序排列。
叶节点都在同一层中。
(1)B树的阶
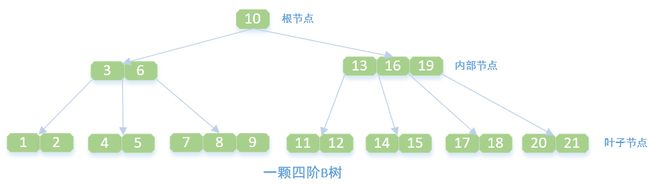
B树中一个节点的子节点数目的最大值,用m表示,假如最大值为4,则为4阶,如图,所有节点中,节点[13,16,19]拥有的子节点数目最多,四个子节点(灰色节点),所以可以定义上面的图片为4阶B树。
(2)根节点
节点【10】即为根节点,特征:根节点拥有的子节点数量的上限和内部节点相同,如果根节点不是树中唯一节点的话,至少有俩个子节点(不然就变成单支了)。在m阶B树中(根节点非树中唯一节点),那么有关系式2<= M <=m,M为子节点数量;包含的元素数量 1<= K <=m-1,K为元素数量。
(3)内部节点
节点【13,16,19】、节点【3,6】都为内部节点,特征:内部节点是除叶子节点和根节点之外的所有节点,拥有父节点和子节点。假定m阶B树的内部节点的子节点数量为M,则一定要符合(m/2)<= M <=m关系式,包含元素数量M-1;包含的元素数量 (m/2)-1<= K <=m-1,K为元素数量。m/2向上取整。
(4)叶子节点
节点【1,2】、节点【11,12】等最后一层都为叶子节点,叶子节点对元素的数量有相同的限制,但是没有子节点,也没有指向子节点的指针。特征:在m阶B树中叶子节点的元素符合(m/2)-1<= K <=m-1。
B树的目的
B树的出现是为了弥补不同的存储级别之间的访问速度上的巨大差异,实现高效的 I/O。平衡二叉树的查找效率是非常高的,并可以通过降低树的深度来提高查找的效率。但是当数据量非常大,树的存储的元素数量是有限的,这样会导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁,进而导致查询效率低下。另外数据量过大会导致内存空间不够容纳平衡二叉树所有结点的情况。B树是解决这个问题的很好的结构。
B树的查找
在B树上进行查找与二叉查找树很相似,只是每个结点都是多个关键字的有序表,在每个结点上所做的不是两路分支决定,而是根据该结点的子树所做的多路分支决定。
B树的查找包含两个基本操作:①在B树中找结点;②在结点内找关键字。由于B树常存储在磁盘上,因此前一个查找操作是在磁盘上进行的,而后一个查找操作是在内存中进行的,即在找到目标结点后,先将结点信息读入内存,然后在结点内采用顺序查找法或折半查找法。
在B树上查找到某个结点后,先在有序表中进行查找,若找到则查找成功,否则按照对应的指针信息到所指的子树中去查找。
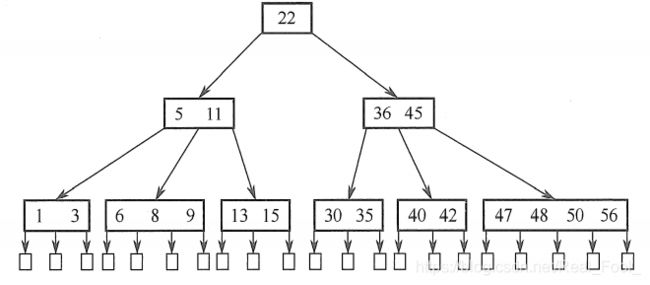
例如,在上图中查找关键字42,首先从根结点开始,根结点只有一个关键字,且42>22,若存在,必在关键字22的右边子树上,右孩子结点有两个关键字,而36<42<45,则若存在,必在36和45中间的子树上,在该子结点中查到关键字42,查找成功。若查找到叶结点时(对应指针为空指针),则说明树中没有对应的关键字,查找失败。
B树的插入
与二叉查找树的插入操作相比,B树的插入操作要复杂得多。在二叉査找树中,仅需査找到需插入的终端结点的位置。但是,在B树中找到插入的位置后,并不能简单地将其添加到终端结点中,因为此时可能会导致整棵树不再满足B树定义中的要求。将关键字key插入B树的过程如下:
1.定位。利用前述的B树査找算法,找出插入该关键字的最低层中的某个非叶结点(在B树中查找key时,会找到表示查找失败的叶结点,这样就确定了最底层非叶结点的插入位置。注意:插入位置一定是最低层中的某个非叶结点)。
2.插入。在B树中,每个非失败结点的关键字个数都在区间[⌈m/2⌉−1,m−1]内。插入后的结点关键字个数小于m,可以直接插入;插入后检查被插入结点内关键字的个数,当插入后的结点关键字个数大于m−1时,必须对结点进行分裂。
分裂的方法是:取一个新结点,在插入key后的原结点,从中间位置⌈m/2⌉将其中的关键字分为两部分,左部分包含的关键字放在原结点中,右部分包含的关键字放到新结点中,中间位置⌈m/2⌉的结点插入原结点的父结点。若此时导致其父结点的关键字个数也超过了上限,则继续进行这种分裂操作,直至这个过程传到根结点为止,进而导致B树高度增1。
对于m=3的B树,所有结点中最多有m−1=2个关键字,若某结点中已有两个关键字,则结点已满,如下图a所示。插入一个关键字60后,结点内的关键字个数超过了m−1,如图b所示,此时必须进行结点分裂,分裂的结果如图c所示。
通俗点讲,B树的插入,结点不溢出时好说,直接插入;如果结点溢出那就分裂,并把中间结点合并到父节点。
B树的删除
B树中的删除操作与插入操作类似,但要更复杂一些,即要使得删除后的结点中的关键字个数≥⌈m/2⌉− 1 ,因此将涉及结点的“合并”问题。
当被删关键字k不在终端结点(最低层非叶结点)中时,可以用k的前驱(或后继) k′来替代k,然后在相应的结点中删除k′,关键字k′必定落在某个终端结点中,则转换成了被删关键字在终端结点中的情形。在下图的B树中,删除关键字80,用其前驱78替代,然后在终端结点中删除78。因此只需讨论删除终端结点中关键字的情形。
当被删关键字在终端结点(最低层非叶结点)中时,有下列三种情况:
① 直接删除关键字。若被删除关键字所在结点的关键字个数≥⌈m/2⌉,表明删除该关键字后仍满足B树的定义,则直接删去该关键字。
② 兄弟够借。若被删除关键字所在结点删除前的关键字个数=⌈m/2⌉−1,且与此结点相邻的右(或左)兄弟结点的关键字个数≥⌈m/2⌉,则需要调整该结点、右(或左)兄弟结点及其双亲结点(父子换位法),以达到新的平衡。在图(a)中删除B树的关键字65,右兄弟关键字个数≥⌈m/2⌉=2,将71取代原65的位置,将74调整到71的位置。
③ 兄弟不够借。若被删除关键字所在结点删除前的关键字个数=⌈m/2⌉−1,且此时与该结点相邻的左、右兄弟结点的关键字个数均=⌈m/2⌉−1,则将关键字删除后与左(或右)兄弟结点及双亲结点中的关键字进行合并。在图(b)中删除B树的关键字5,它及其右兄弟结点的关键字个数=⌈m/2⌉−1=1,故在5删除后将60合并到65结点中。
在合并过程中,双亲结点中的关键字个数会减1。若其双亲结点是根结点且关键字个数减少至0 (根结点关键字个数为1时,有2棵子树),则直接将根结点删除,合并后的新结点成为根;若双亲结点不是根结点,且关键字个数减少到⌈m/2⌉−2,则又要与它自己的兄弟结点进行调整或合并操作,并重复上述步骤,直至符合B树的要求为止。
其实通俗点讲,B树的删除,删除结点无非就是多留少补的情况,多留不必多说;少补复杂点:当兄弟够借时,就向左旋转一次(即往左挪一个位置,重构根节点关键字的前驱和后继);当兄弟不够借时就拆根节点,合并到兄弟结点,合并拆分要始终保证B树平衡,理清了就很容易理解。
完整代码
#ifndef _BTREE_H
#define _BTREE_H
#define MAXM 10 //定义B树的最大的阶数
const int m=5; //设定B树的阶数
const int Max=m-1; //结点的最大关键字数量
const int Min=(m-1)/2; //结点的最小关键字数量
typedef int KeyType; //KeyType为关键字类型
typedef struct node{ //B树和B树结点类型
int keynum; //结点关键字个数
KeyType key[MAXM]; //关键字数组,key[0]不使用
struct node *parent; //双亲结点指针
struct node *ptr[MAXM]; //孩子结点指针数组
}BTNode,*BTree;
typedef struct{ //B树查找结果类型
BTNode *pt; //指向找到的结点
int i; //在结点中的关键字位置;
int tag; //查找成功与否标志
}Result;
typedef struct LNode{ //链表和链表结点类型
BTree data; //数据域
struct LNode *next; //指针域
}LNode, *LinkList;
typedef enum status{ //枚举类型(依次递增)
TRUE,
FALSE,
OK,
ERROR,
OVERFLOW,
EMPTY
}Status;
Status InitBTree(BTree &t); //初始化B树
int SearchBTNode(BTNode *p,KeyType k); //在结点p中查找关键字k的插入位置i
Result SearchBTree(BTree t,KeyType k); /*在树t上查找关键字k,返回结果(pt,i,tag)。若查找成功,则特征值
tag=1,关键字k是指针pt所指结点中第i个关键字;否则特征值tag=0,
关键字k的插入位置为pt结点的第i个*/
void InsertBTNode(BTNode *&p,int i,KeyType k,BTNode *q); //将关键字k和结点q分别插入到p->key[i+1]和p->ptr[i+1]中
void SplitBTNode(BTNode *&p,BTNode *&q); //将结点p分裂成两个结点,前一半保留,后一半移入结点q
void NewRoot(BTNode *&t,KeyType k,BTNode *p,BTNode *q); //生成新的根结点t,原结点p和结点q为子树指针
void InsertBTree(BTree &t,int i,KeyType k,BTNode *p); /*在树t上结点q的key[i]与key[i+1]之间插入关键字k。若引起
结点过大,则沿双亲链进行必要的结点分裂调整,使t仍是B树*/
void Remove(BTNode *p,int i); //从p结点删除key[i]和它的孩子指针ptr[i]
void Substitution(BTNode *p,int i); //查找被删关键字p->key[i](在非叶子结点中)的替代叶子结点(右子树中值最小的关键字)
void MoveRight(BTNode *p,int i); /*将双亲结点p中的最后一个关键字移入右结点q中
将左结点aq中的最后一个关键字移入双亲结点p中*/
void MoveLeft(BTNode *p,int i); /*将双亲结点p中的第一个关键字移入结点aq中,
将结点q中的第一个关键字移入双亲结点p中*/
void Combine(BTNode *p,int i); /*将双亲结点p、右结点q合并入左结点aq,
并调整双亲结点p中的剩余关键字的位置*/
void AdjustBTree(BTNode *p,int i); //删除结点p中的第i个关键字后,调整B树
int FindBTNode(BTNode *p,KeyType k,int &i); //反映是否在结点p中是否查找到关键字k
int BTNodeDelete(BTNode *p,KeyType k); //在结点p中查找并删除关键字k
void BTreeDelete(BTree &t,KeyType k); //构建删除框架,执行删除操作
void DestroyBTree(BTree &t); //递归释放B树
Status InitQueue(LinkList &L); //初始化队列
LNode* CreateNode(BTree t); //新建一个结点
Status Enqueue(LNode *p,BTree t); //元素q入队列
Status Dequeue(LNode *p,BTNode *&q); //出队列,并以q返回值
Status IfEmpty(LinkList L); //队列判空
void DestroyQueue(LinkList L); //销毁队列
Status Traverse(BTree t,LinkList L,int newline,int sum); //用队列遍历输出B树
Status PrintBTree(BTree t); //输出B树
void Test(); //测试B树功能函数
#endif
#include
#include
#include
Status InitBTree(BTree &t){
//初始化B树
t=NULL;
return OK;
}
int SearchBTNode(BTNode *p,KeyType k){
//在结点p中查找关键字k的插入位置i
int i=0;
for(i=0;ikeynum&&p->key[i+1]<=k;i++);
return i;
}
Result SearchBTree(BTree t,KeyType k){
/*在树t上查找关键字k,返回结果(pt,i,tag)。若查找成功,则特征值
tag=1,关键字k是指针pt所指结点中第i个关键字;否则特征值tag=0,
关键字k的插入位置为pt结点的第i个*/
BTNode *p=t,*q=NULL; //初始化结点p和结点q,p指向待查结点,q指向p的双亲
int found_tag=0; //设定查找成功与否标志
int i=0;
Result r; //设定返回的查找结果
while(p!=NULL&&found_tag==0){
i=SearchBTNode(p,k); //在结点p中查找关键字k,使得p->key[i]<=kkey[i+1]
if(i>0&&p->key[i]==k) //找到待查关键字
found_tag=1; //查找成功
else{ //查找失败
q=p;
p=p->ptr[i];
}
}
if(found_tag==1){ //查找成功
r.pt=p;
r.i=i;
r.tag=1;
}
else{ //查找失败
r.pt=q;
r.i=i;
r.tag=0;
}
return r; //返回关键字k的位置(或插入位置)
}
void InsertBTNode(BTNode *&p,int i,KeyType k,BTNode *q){
//将关键字k和结点q分别插入到p->key[i+1]和p->ptr[i+1]中
int j;
for(j=p->keynum;j>i;j--){ //整体后移空出一个位置
p->key[j+1]=p->key[j];
p->ptr[j+1]=p->ptr[j];
}
p->key[i+1]=k;
p->ptr[i+1]=q;
if(q!=NULL)
q->parent=p;
p->keynum++;
}
void SplitBTNode(BTNode *&p,BTNode *&q){
//将结点p分裂成两个结点,前一半保留,后一半移入结点q
int i;
int s=(m+1)/2;
q=(BTNode *)malloc(sizeof(BTNode)); //给结点q分配空间
q->ptr[0]=p->ptr[s]; //后一半移入结点q
for(i=s+1;i<=m;i++){
q->key[i-s]=p->key[i];
q->ptr[i-s]=p->ptr[i];
}
q->keynum=p->keynum-s;
q->parent=p->parent;
for(i=0;i<=p->keynum-s;i++) //修改双亲指针
if(q->ptr[i]!=NULL)
q->ptr[i]->parent=q;
p->keynum=s-1; //结点p的前一半保留,修改结点p的keynum
}
void NewRoot(BTNode *&t,KeyType k,BTNode *p,BTNode *q){
//生成新的根结点t,原p和q为子树指针
t=(BTNode *)malloc(sizeof(BTNode)); //分配空间
t->keynum=1;
t->ptr[0]=p;
t->ptr[1]=q;
t->key[1]=k;
if(p!=NULL) //调整结点p和结点q的双亲指针
p->parent=t;
if(q!=NULL)
q->parent=t;
t->parent=NULL;
}
void InsertBTree(BTree &t,int i,KeyType k,BTNode *p){
/*在树t上结点q的key[i]与key[i+1]之间插入关键字k。若引起
结点过大,则沿双亲链进行必要的结点分裂调整,使t仍是B树*/
BTNode *q;
int finish_tag,newroot_tag,s; //设定需要新结点标志和插入完成标志
KeyType x;
if(p==NULL) //t是空树
NewRoot(t,k,NULL,NULL); //生成仅含关键字k的根结点t
else{
x=k;
q=NULL;
finish_tag=0;
newroot_tag=0;
while(finish_tag==0&&newroot_tag==0){
InsertBTNode(p,i,x,q); //将关键字x和结点q分别插入到p->key[i+1]和p->ptr[i+1]
if (p->keynum<=Max)
finish_tag=1; //插入完成
else{
s=(m+1)/2;
SplitBTNode(p,q); //分裂结点
x=p->key[s];
if(p->parent){ //查找x的插入位置
p=p->parent;
i=SearchBTNode(p, x);
}
else //没找到x,需要新结点
newroot_tag=1;
}
}
if(newroot_tag==1) //根结点已分裂为结点p和q
NewRoot(t,x,p,q); //生成新根结点t,p和q为子树指针
}
}
void Remove(BTNode *p,int i){
//从p结点删除key[i]和它的孩子指针ptr[i]
int j;
for(j=i+1;j<=p->keynum;j++){ //前移删除key[i]和ptr[i]
p->key[j-1]=p->key[j];
p->ptr[j-1]=p->ptr[j];
}
p->keynum--;
}
void Substitution(BTNode *p,int i){
//查找被删关键字p->key[i](在非叶子结点中)的替代叶子结点(右子树中值最小的关键字)
BTNode *q;
for(q=p->ptr[i];q->ptr[0]!=NULL;q=q->ptr[0]);
p->key[i]=q->key[1]; //复制关键字值
}
void MoveRight(BTNode *p,int i){
/*将双亲结点p中的最后一个关键字移入右结点q中
将左结点aq中的最后一个关键字移入双亲结点p中*/
int j;
BTNode *q=p->ptr[i];
BTNode *aq=p->ptr[i-1];
for(j=q->keynum;j>0;j--){ //将右兄弟q中所有关键字向后移动一位
q->key[j+1]=q->key[j];
q->ptr[j+1]=q->ptr[j];
}
q->ptr[1]=q->ptr[0]; //从双亲结点p移动关键字到右兄弟q中
q->key[1]=p->key[i];
q->keynum++;
p->key[i]=aq->key[aq->keynum]; //将左兄弟aq中最后一个关键字移动到双亲结点p中
p->ptr[i]->ptr[0]=aq->ptr[aq->keynum];
aq->keynum--;
}
void MoveLeft(BTNode *p,int i){
/*将双亲结点p中的第一个关键字移入左结点aq中,
将右结点q中的第一个关键字移入双亲结点p中*/
int j;
BTNode *aq=p->ptr[i-1];
BTNode *q=p->ptr[i];
aq->keynum++; //把双亲结点p中的关键字移动到左兄弟aq中
aq->key[aq->keynum]=p->key[i];
aq->ptr[aq->keynum]=p->ptr[i]->ptr[0];
p->key[i]=q->key[1]; //把右兄弟q中的关键字移动到双亲节点p中
q->ptr[0]=q->ptr[1];
q->keynum--;
for(j=1;j<=aq->keynum;j++){ //将右兄弟q中所有关键字向前移动一位
aq->key[j]=aq->key[j+1];
aq->ptr[j]=aq->ptr[j+1];
}
}
void Combine(BTNode *p,int i){
/*将双亲结点p、右结点q合并入左结点aq,
并调整双亲结点p中的剩余关键字的位置*/
int j;
BTNode *q=p->ptr[i];
BTNode *aq=p->ptr[i-1];
aq->keynum++; //将双亲结点的关键字p->key[i]插入到左结点aq
aq->key[aq->keynum]=p->key[i];
aq->ptr[aq->keynum]=q->ptr[0];
for(j=1;j<=q->keynum;j++){ //将右结点q中的所有关键字插入到左结点aq
aq->keynum++;
aq->key[aq->keynum]=q->key[j];
aq->ptr[aq->keynum]=q->ptr[j];
}
for(j=i;jkeynum;j++){ //将双亲结点p中的p->key[i]后的所有关键字向前移动一位
p->key[j]=p->key[j+1];
p->ptr[j]=p->ptr[j+1];
}
p->keynum--; //修改双亲结点p的keynum值
free(q); //释放空右结点q的空间
}
void AdjustBTree(BTNode *p,int i){
//删除结点p中的第i个关键字后,调整B树
if(i==0) //删除的是最左边关键字
if(p->ptr[1]->keynum>Min) //右结点可以借
MoveLeft(p,1);
else //右兄弟不够借
Combine(p,1);
else if(i==p->keynum) //删除的是最右边关键字
if(p->ptr[i-1]->keynum>Min) //左结点可以借
MoveRight(p,i);
else //左结点不够借
Combine(p,i);
else if(p->ptr[i-1]->keynum>Min) //删除关键字在中部且左结点够借
MoveRight(p,i);
else if(p->ptr[i+1]->keynum>Min) //删除关键字在中部且右结点够借
MoveLeft(p,i+1);
else //删除关键字在中部且左右结点都不够借
Combine(p,i);
}
int FindBTNode(BTNode *p,KeyType k,int &i){
//反映是否在结点p中是否查找到关键字k
if(kkey[1]){ //结点p中查找关键字k失败
i=0;
return 0;
}
else{ //在p结点中查找
i=p->keynum;
while(kkey[i]&&i>1)
i--;
if(k==p->key[i]) //结点p中查找关键字k成功
return 1;
}
}
int BTNodeDelete(BTNode *p,KeyType k){
//在结点p中查找并删除关键字k
int i;
int found_tag; //查找标志
if(p==NULL)
return 0;
else{
found_tag=FindBTNode(p,k,i); //返回查找结果
if(found_tag==1){ //查找成功
if(p->ptr[i-1]!=NULL){ //删除的是非叶子结点
Substitution(p,i); //寻找相邻关键字(右子树中最小的关键字)
BTNodeDelete(p->ptr[i],p->key[i]); //执行删除操作
}
else
Remove(p,i); //从结点p中位置i处删除关键字
}
else
found_tag=BTNodeDelete(p->ptr[i],k); //沿孩子结点递归查找并删除关键字k
if(p->ptr[i]!=NULL)
if(p->ptr[i]->keynumkeynum==0){ //调整
p=t;
t=t->ptr[0];
free(p);
}
}
void DestroyBTree(BTree &t){
//递归释放B树
int i;
BTNode* p=t;
if(p!=NULL){ //B树不为空
for(i=0;i<=p->keynum;i++){ //递归释放每一个结点
DestroyBTree(*&p->ptr[i]);
}
free(p);
}
t=NULL;
}
Status InitQueue(LinkList &L){
//初始化队列
L=(LNode*)malloc(sizeof(LNode)); //分配结点空间
if(L==NULL) //分配失败
return OVERFLOW;
L->next=NULL;
return OK;
}
LNode* CreateNode(BTNode *p){
//新建一个结点
LNode *q;
q=(LNode*)malloc(sizeof(LNode)); //分配结点空间
if(q!=NULL){ //分配成功
q->data=p;
q->next=NULL;
}
return q;
}
Status Enqueue(LNode *p,BTNode *q){
//元素q入队列
if(p==NULL)
return ERROR;
while(p->next!=NULL) //调至队列最后
p=p->next;
p->next=CreateNode(q); //生成结点让q进入队列
return OK;
}
Status Dequeue(LNode *p,BTNode *&q){
//出队列,并以q返回值
LNode *aq;
if(p==NULL||p->next==NULL) //删除位置不合理
return ERROR;
aq=p->next; //修改被删结点aq的指针域
p->next=aq->next;
q=aq->data;
free(aq); //释放结点aq
return OK;
}
Status IfEmpty(LinkList L){
//队列判空
if(L==NULL) //队列不存在
return ERROR;
if(L->next==NULL) //队列为空
return TRUE;
return FALSE; //队列非空
}
void DestroyQueue(LinkList L){
//销毁队列
LinkList p;
if(L!=NULL){
p=L;
L=L->next;
free(p); //逐一释放
DestroyQueue(L);
}
}
Status Traverse(BTree t,LinkList L,int newline,int sum){
//用队列遍历输出B树
int i;
BTree p;
if(t!=NULL){
printf(" [ ");
Enqueue(L,t->ptr[0]); //入队
for(i=1;i<=t->keynum;i++){
printf(" %d ",t->key[i]);
Enqueue(L,t->ptr[i]); //子结点入队
}
sum+=t->keynum+1;
printf("]");
if(newline==0){ //需要另起一行
printf("\n");
newline=sum-1;
sum=0;
}
else
newline--;
}
if(IfEmpty(L)==FALSE){ //l不为空
Dequeue(L,p); //出队,以p返回
Traverse(p,L,newline,sum); //遍历出队结点
}
return OK;
}
Status PrintBTree(BTree t){
//输出B树
LinkList L;
if(t==NULL){
printf(" B树为空树");
return OK;
}
InitQueue(L); //初始化队列
Traverse(t,L,0,0); //利用队列输出
DestroyQueue(L); //销毁队列
return OK;
}
void Test1(){
system("color 70");
BTNode *t=NULL;
Result s; //设定查找结果
int j,n=15;
KeyType k;
KeyType a[]={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15};
printf("创建一棵%d阶B树:\n",m);
for(j=0;j B+树
B+树的定义
一颗m阶的B+树满足如下条件:
每个节点最多只有m个子节点。
除根节点外,每个非叶子节点具有至少有 m/2(向下取整)个子节点。
非叶子节点的根节点至少有两个子节点。
有k颗子树的非叶节点有k个键,键按照递增顺序排列。
叶节点都在同一层中。
说明:
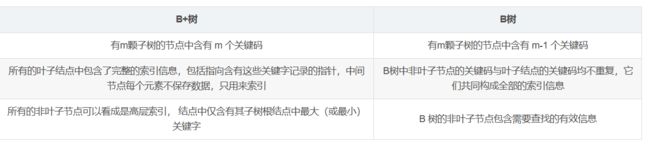
每个叶节点中至少包含 m/2(向下取整)个关键码,所有主文件记录的索引项都存放在B+树的叶节点中。所有内部节点都看成是索引的索引。节点中仅包含它的各个子节点中最大(或最小)关键码的分界值以及指向子节点的指针。
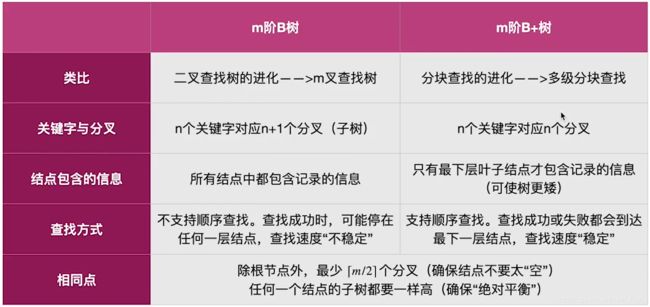
在B+树中,每个结点(非根内部结点)的关键字个数n的范围是⌈m/2⌉≤n≤m(根结点:1≤n≤m);在B树中,每个结点(非根内部结点)的关键字个数n nn范围是⌈m/2⌉−1≤n≤m−1 (根结点: 1≤n≤m−1)。
查询
在B+树中检索关键码key的方法与B树的检索方式相似,但若在内部节点中找到检索的关键码时,检索并不会结束,要继续找到B+树的叶子结点为止。
插入
与B树的插入操作相似,总是插到叶子结点上。当叶节点中原关键码的个数等于m时,该节点分裂成两个节点,分别使关键码的个数为 (m+1)/2 (向上取整)和 (m+1)/2 (向下取整)。
删除
仅在叶节点删除关键码。若因为删除操作使得节点中关键码数少于 m/2(向下取整)时,则需要调整或者和兄弟节点合并。合并的过程和B树类似,区别是父节点中作为分界的关键码不放入合并后的节点中。
下图所示为一棵4阶B+树。
B+树的结构特别适合带有范围的查找。比如查找我们学校18~22岁的学生人数,我们可以通过从根结点出发找到第一个18岁的学生,然后再在叶子结点按顺序查找到符合范围的所有记录。
B+树的插入、删除过程也都与B树类似,只不过插入和删除的元素都是在叶子结点上进行而已。