swift算法：买卖股票的最佳时机II

1、描述

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润，你可以尽可能的完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

例1：输入：[7, 1, 5, 3, 6, 4]

         输出：7

         解释：在第2天（股票价格=1）的时候买入，在第3天（股票价格=5）的时候卖出，这笔交易所能获得利润=5-1=4

                   随后，在第4天（股票价格=3）的时候买入，在第5天（股票价格=6）的时候卖出，这笔交易所能获得利润=6-3=3

例1：输入：[1, 2, 3, 4, 5]

         输出：4

         解释： 在第1天（股票价格=1）的时候买入，在第5天（股票价格=5）的时候卖出，这笔交易所能获得利润=5-1=4

                       注意你不能在第1天和地2天接连购买股票，之后再将它们卖出。

                       因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

 

2、算法

1）暴力法

思想：利用递归，遍历计算所有可能的交易组合相对应的利润且相加

时间复杂度：O(n^n)

func maxProfitII(_ prices: [Int]) -> Int {
        /*
         暴力法
         */
        return calculate(prices, 0)
    }
    private func calculate(_ prices : [Int], _ s : Int)->Int{
        if s >= prices.count {
            return 0
        }
        var max = 0
        for start in s.. maxpfrofit{
                        maxpfrofit = profit
                    }
                }
            }
            if maxpfrofit > max {
                max = maxpfrofit
            }
        }
        return max
    }

2）一次遍历

思想：在斜坡上爬升并持续增加从连续交易中获得的利润

图示[1, 7, 2, 3, 6, 7, 6, 7]，所求即为 A+B+C  = D

时间复杂度：：O(n)

func maxProfitII(_ prices: [Int]) -> Int {
        /*
         一次遍历
         */
        if prices.count==0 || prices.count==1{
            return 0
        }
        var maxprofit : Int = 0
        for i in 1.. prices[i-1] {
                maxprofit += prices[i] - prices[i-1]
            }
        }
        return maxprofit
    }

3）峰谷法

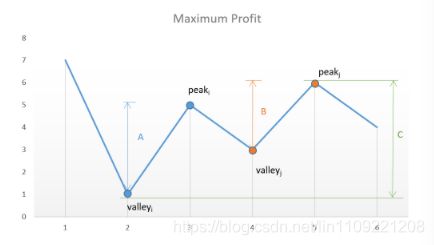
思想：计算峰谷与山顶的最大距离即为最大利润

图示 [7, 1, 5, 3, 6, 4]，c即为所求的最大利润

时间复杂度：O(n)

func maxProfitII(_ prices: [Int]) -> Int {
        /*
         峰谷法：
         TotalProfit=∑下i(height(peak下i)−height(valley下i))
         */
        if prices.count==0 || prices.count==1{
            return 0
        }
        var maxprofit : Int = 0
        var valley = prices[0]
        var peak = prices[0]
        var i = 0
        while i < prices.count-1 {
            while i < prices.count-1 && prices[i]>=prices[i+1]{
                i += 1
            }
            valley = prices[i]
            while i < prices.count-1 && prices[i] <= prices[i+1]{
                i += 1
            }
            peak = prices[i]
            maxprofit += peak - valley
        }
        return maxprofit
    }