使用的面向对象方式编写,主要类是Cart类,直接传入数据和属性集合,然后draw就可以
运行结果如下(每次运行属性值顺序可能会不同,由于hash问题,不用管,结果是一样的)
全部代码可下载项目https://gitee.com/TomCoCo/mLearn.git
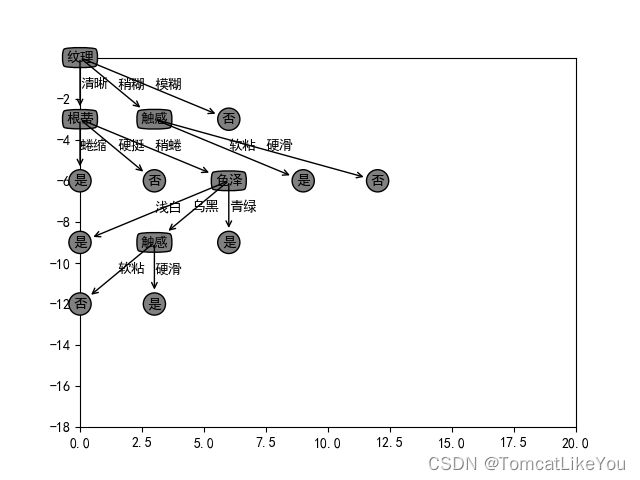
这里是代码,有完整的注释,可以直接运行如上图
核心方法 createTree
import math
import matplotlib.pyplot as plt
import copy
D = [
['青绿','蜷缩','浊响','清晰','凹陷','硬滑','是'],
['乌黑','蜷缩','沉闷','清晰','凹陷','硬滑','是'],
['乌黑','蜷缩','浊响','清晰','凹陷','硬滑','是'],
['青绿','蜷缩','沉闷','清晰','凹陷','硬滑','是'],
['浅白','蜷缩','浊响','清晰','凹陷','硬滑','是'],
['青绿','稍蜷','浊响','清晰','稍凹','软粘','是'],
['乌黑','稍蜷','浊响','稍糊','稍凹','软粘','是'],
['乌黑','稍蜷','浊响','清晰','稍凹','硬滑','是'],
['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑','否'],
['青绿','硬挺','清脆','清晰','平坦','软粘','否'],
['浅白','硬挺','清脆','模糊','平坦','硬滑','否'],
['浅白','蜷缩','浊响','模糊','平坦','软粘','否'],
['青绿','稍蜷','浊响','稍糊','凹陷','硬滑','否'],
['浅白','稍蜷','沉闷','稍糊','凹陷','硬滑','否'],
['乌黑','稍蜷','浊响','清晰','稍凹','软粘','否'],
['浅白','蜷缩','浊响','模糊','平坦','硬滑','否'],
['青绿','蜷缩','沉闷','稍糊','稍凹','硬滑','否']
]
A = ['色泽','根蒂','敲声','纹理','脐部','触感','好瓜']
class Cart:
data = None
attributes = None
attributesAndIndex = None
attributesIndexAndValue = None
root = None
def __init__(self,data,attributes):
self.data = data
self.attributes = attributes
self.attributesAndIndex = Cart.getAttributesAndIndex(attributes)
self.attributesIndexAndValue = Cart.getAttributesAndValue(data,attributes)
def draw(self):
self.createTree(self.root,self.data,self.attributesAndIndex,None)
tree = Tree(self.root)
tree.drawTree()
def createTree(self,node,data,attributesAndIndex,desc):
newNode = Node()
if(desc is not None):
newNode.desc = desc
if node is None:
self.root = newNode
else:
node.addChild(newNode)
kMap = Cart.getKMap(data)
if len(kMap) == 1:
newNode.name = next(iter(kMap.keys()))
return
if Cart.checkDA(data,attributesAndIndex):
newNode.name = Cart.getMoreType(data)
return
bestIndex = Cart.getMinGiniIndexStrict(data,attributesAndIndex)
newNode.name = self.attributes[bestIndex]
aStart = self.attributesIndexAndValue[bestIndex]
V = Cart.splitDataByIndex(data,bestIndex)
for aStartV in aStart:
dv = V.get(aStartV)
if dv is None or len(dv) == 0:
newLeaf = Node()
newLeaf.name = Cart.getMoreType(data)
newLeaf.desc = aStartV
newNode.addChild(newLeaf)
else:
Anew = copy.deepcopy(attributesAndIndex)
for index,item in enumerate(Anew):
if next(iter(item.values())) == bestIndex:
Anew.pop(index)
break
self.createTree(newNode,dv,Anew,aStartV)
@staticmethod
def checkDA(data,attributesAndIndex):
if len(attributesAndIndex) == 0:
return True
for item in attributesAndIndex:
nowAttributesValue = None
aIndex = next(iter(item.values()))
for dLine in data:
if nowAttributesValue == None:
nowAttributesValue = dLine[aIndex]
elif nowAttributesValue != dLine[aIndex]:
return False
return True;
@staticmethod
def getAttributesAndIndex(attributes):
attributesAndIndex = list()
for index,attribute in enumerate(attributes):
attributesAndIndex.append({attribute:index})
return attributesAndIndex[:len(attributesAndIndex) - 1]
@staticmethod
def getAttributesAndValue(data,attributes):
attributesAndValue = dict()
for dLine in data:
for i in range(len(attributes) - 1):
v = attributesAndValue.get(i)
if v == None:
v = set()
attributesAndValue[i] = v
v.add(dLine[i])
return attributesAndValue
@staticmethod
def getMinGiniIndexStrict(data,attributesAndIndex):
minGiniIndex = None
minIndex = None
for item in attributesAndIndex:
aName = next(iter(item.keys()))
aIndex = next(iter(item.values()))
giniIndex = Cart.getGiniIndex(data,aIndex)
if minGiniIndex == None or giniIndex < minGiniIndex:
minGiniIndex = giniIndex
minIndex = aIndex
print("第" , aIndex ,"列的属性",aName,"的基尼指数为:" , giniIndex)
print("第" , minIndex ,"列的属性",aName,"的基尼指数最小为:" , minGiniIndex ,";为最优划分属性")
return minIndex
@staticmethod
def getMinGiniIndex(data,attributes):
attributesSize = len(attributes) - 1
i = 0
minGiniIndex = None
minIndex = None
while i < attributesSize:
giniIndex = Cart.getGiniIndex(data,i)
if minGiniIndex == None or giniIndex < minGiniIndex:
minGiniIndex = giniIndex
minIndex = i
print("第" , i ,"列的属性",attributes[i],"的基尼指数为:" , giniIndex)
i += 1
print("第" , minIndex ,"列的属性",attributes[minIndex],"的基尼指数最小为:" , minGiniIndex ,";为最优划分属性")
return minIndex
@staticmethod
def getGiniIndex(data,attributesIndex):
V = Cart.splitDataByIndex(data,attributesIndex)
dSize = len(data)
rs = 0
for Dv in V.values():
dvSize = len(Dv)
dvGini = Cart.getGini(Cart.getKMap(Dv),dvSize)
rs += (dvSize/dSize) * dvGini
return rs
@staticmethod
def splitDataByIndex(data,attributesIndex):
V = dict()
for dLine in data:
attribute = dLine[attributesIndex]
Dv = V.get(attribute)
if Dv is None:
Dv = list()
V[attribute] = Dv
Dv.append(dLine)
return V
@staticmethod
def getGini(kMap,dSize):
rs = 0
for item in kMap.values():
pk = (item/dSize)
rs += pk * pk
return 1 - rs
@staticmethod
def getMoreType(data):
kMap = Cart.getKMap(data)
maxCount = -1
maxName = None
for key in kMap.keys():
if kMap.get(key) > maxCount:
maxCount = kMap.get(key)
maxName = key
return maxName
@staticmethod
def getKMap(data):
kMap = dict()
for dLine in data:
k = dLine[len(dLine) - 1]
kNum = kMap.get(k)
if kNum is None:
kMap[k] = 1
else:
kMap[k] = kNum + 1
return kMap
class Node:
name = "未命名节点"
desc = ""
children = []
def __init__(self):
self.children = []
def addChild(self, node):
self.children.append(node)
class Tree:
root = None
decisionNode = dict(boxstyle="round4", fc="0.5")
leafNode = dict(boxstyle="circle", fc="0.5")
arrow_args = dict(arrowstyle="<-")
step = 3
deep = 0
nowDeepIndex = 0
deepIndex = dict()
def __init__(self, root):
self.root = root
plt.xlim(0, 20)
plt.ylim(-18, 0)
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
def drawLeaf(self, x1, y1, x2, y2, text, desc):
plt.annotate(text,
xy=(x1, y1),
xytext=(x2, y2),
va='center',
ha='center',
xycoords="data",
textcoords='data',
bbox=self.leafNode,
arrowprops=self.arrow_args)
plt.text((x1 + x2) / 2, (y1 + y2) / 2, desc)
def drawDecision(self, x1, y1, x2, y2, text, desc):
plt.annotate(text,
xy=(x1, y1),
xytext=(x2, y2),
va='center',
ha='center',
xycoords="data",
textcoords='data',
bbox=self.decisionNode,
arrowprops=self.arrow_args)
plt.text((x1 + x2) / 2, (y1 + y2) / 2, desc)
def drawRoot(self, text):
plt.annotate(text,
xy=(0, 0),
va='center',
ha='center',
xycoords="data",
textcoords='data',
bbox=self.decisionNode)
def drawTree(self):
self.draw0(self.root, 0, 0)
plt.show()
def draw0(self, node, x, y):
if(self.deepIndex.get(self.deep) is None):
self.deepIndex[self.deep] = 0
x2 = self.deepIndex[self.deep] * self.step
y2 = y - self.step
if len(node.children) > 0:
if len(node.desc) > 0:
self.drawDecision(x, y, x2, y2, node.name, node.desc)
self.deep += 1
for i, child in enumerate(node.children):
self.draw0(child, x2, y2)
self.deep -= 1
else:
self.drawRoot(node.name)
for i, child in enumerate(node.children):
self.draw0(child, 0, 0)
else:
self.drawLeaf(x, y, x2, y2, node.name, node.desc)
self.deepIndex[self.deep] = self.deepIndex[self.deep] + 1
cart = Cart(D,A)
cart.draw()
