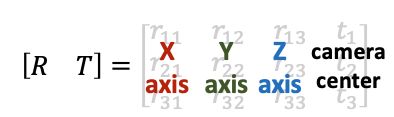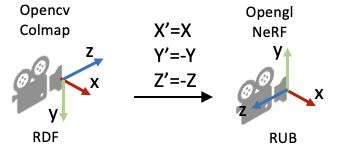神经辐射场(NeRF)中-相机参数与坐标系变换
NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis 是一篇获得ECCV2020 Best Paper Honorable Mention的论文。给定一个场景的多视角的图像,神经辐射场(NeRF)通过图像重建误差优化一个神经场景表征。优化后可以实现逼真的新视角合成效果。被其逼真的图像合成效果所吸引,很多研究人员开始跟进该方向,并在最近的一两年时间里产生了大量的(好几百篇!)改进和拓展工作。
为什么写这篇文章
网上已经有不少介绍NeRF的文章,这些文章很好地介绍了NeRF论文的核心思想,体素渲染的细节,网络结构,优化策略等等。我这里主要介绍代码实现中关于相机参数以及坐标系变换相关的内容,这个地方是我觉得初学者容易困惑的地方,特别是没有3D知识基础的读者。
本文的代码讲解以pytorch版本的实现为例:https://github.com/yenchenlin/nerf-pytorch。这里假设读者已经看过NeRF论文,并且简单浏览过NeRF的代码。
总体概览
NeRF的技术其实很简洁,并不复杂。但与2D视觉里考虑的2维图像不同,NeRF考虑的是一个3D空间。下面列的是NeRF实现的几个关键部分:
- 有一个3D空间,用一个连续的场表示
- 空间里存在一个感兴趣的物体区域
- 处于不同位置和朝向的相机拍摄多视角图像
- 对于一张图像,根据相机中心和图像平面的一个像素点,两点确定一条射线穿过3D空间
- 在射线上采样多个离散的3D点并利用体素渲染像素的颜色。
这里面涉及到3D空间、物体区域、相机位置和朝向、图像、射线、以及3D采样点等。要想优化NeRF,我们需要能够表达刚刚提到的这些东西。
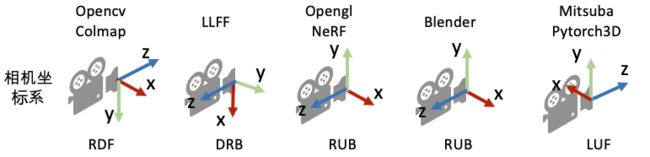
坐标系定义: 为了唯一地描述每一个空间点的坐标,以及相机的位置和朝向,我们需要先定义一个世界坐标系。一个坐标系其实就是由原点的位置与XYZ轴的方向决定。接着,为了建立3D空间点到相机平面的映射关系以及多个相机之间的相对关系,我们会对每一个相机定义一个局部的相机坐标系。下图为常见的坐标系定义习惯。
常见的相机坐标系定义习惯(右手坐标系)。注意:在OpenCV/COLMAP的相机坐标系里相机朝向+z轴,在LLFF/NeRF的相机坐标系中里相机朝向-z轴。有时我们会按坐标系的xyz朝向描述坐标系,如OpenCV/COLMAP里使用的RDF表述X轴指向right,Y轴指向Down,Z轴指向Foward。
相机的内外参数
相机的位置和朝向由相机的外参(extrinsic matrix)决定,投影属性由相机的内参(intrinsic matrix)决定。
注意:接下来的介绍假设矩阵是列矩阵(column-major matrix),变换矩阵左乘坐标向量实现坐标变换(这也是OpenCV/OpenGL/NeRF里使用的形式)。
相机外参
相机外参是一个4x4的矩阵 �,其作用是将世界坐标系的点 ������=[�,�,�,1] 变换到相机坐标系 �������=������� 下。我们也把相机外参叫做world-to-camera (w2c)矩阵。(注意用的是4维的齐次坐标,如果不了解齐次坐标系请自行查阅相关资料。)
相机外参的逆矩阵被称为camera-to-world (c2w)矩阵,其作用是把相机坐标系的点变换到世界坐标系。因为NeRF主要使用c2w,这里详细介绍一下c2w的含义。c2w矩阵是一个4x4的矩阵,左上角3x3是旋转矩阵R,右上角的3x1向量是平移向量T。有时写的时候可以忽略最后一行[0,0,0,1]。
Camera-to-world (c2w) 矩阵
刚刚接触的时候,对这个c2w矩阵的值可能会比较陌生。其实c2w矩阵的值直接描述了相机坐标系的朝向和原点:
理解Camera-to-world (c2w)矩阵
具体的,旋转矩阵的第一列到第三列分别表示了相机坐标系的X, Y, Z轴在世界坐标系下对应的方向;平移向量表示的是相机原点在世界坐标系的对应位置。
如果这段描述还是有点抽象,可以尝试进行下列计算帮助自己理解。刚刚讲到c2w是将相机坐标系的向量变换到世界坐标系下,那我们如果将c2w作用到(即左乘)相机坐标系下的X轴[1,0,0,0],Y轴[0,1,0,0], Z轴[0,0,1,0],以及原点[0,0,0,1](注意方向向量的齐次坐标第四维等于0,点坐标第四维等于1),我们会得到它们在世界坐标系的坐标表示:
[R, T][1, 0, 0, 0]^T = [r11, r21, r31]^T # X轴对应的是c2w矩阵的第一列
[R, T][0, 1, 0, 0]^T = [r12, r22, r32]^T # Y轴对应的是c2w矩阵的第二列
[R, T][0, 0, 1, 0]^T = [r13, r23, r33]^T # Y轴对应的是c2w矩阵的第三列
[R, T][0, 0, 0, 1]^T = [t1, t2, t3]^T # 原点对应的是c2w矩阵的第四列从上面可以看到可以看到,将c2w作用到相机坐标系下的X轴、Y轴、 Z轴、以及原点我们会依次得到c2w的四列向量。
相机内参
刚刚介绍了相机的外参,现在简单介绍一下相机的内参。
相机的内参矩阵将相机坐标系下的3D坐标映射到2D的图像平面,这里以针孔相机(Pinhole camera)为例介绍相机的内参矩阵K:
针孔相机的内参矩阵
内参矩阵K包含4个值,其中fx和fy是相机的水平和垂直焦距(对于理想的针孔相机,fx=fy)。焦距的物理含义是相机中心到成像平面的距离,长度以像素为单位。cx和cy是图像原点相对于相机光心的水平和垂直偏移量。cx,cy有时候可以用图像宽和高的1/2近似:
# NeRF run_nerf.py有这么一段构造K的代码
if K is None:
K = np.array([
[focal, 0, 0.5*W],
[0, focal, 0.5*H],
[0, 0, 1]
])如何获得相机参数
NeRF算法假设相机的内外参数是提供的,那么怎么得到所需要的相机参数呢?这里分合成数据集和真实数据集两种情况。
合成数据
对于合成数据集,我们需要通过指定相机参数来渲染图像,所以得到图像的时候已经知道对应的相机参数,比如像NeRF用到的Blender Lego数据集。常用的渲染软件还有Mitsuba、OpenGL、PyTorch3D、Pyrender等。渲染数据比较简单,但是把得到的相机数据转到NeRF代码坐标系牵扯到坐标系之间的变换,有时候会比较麻烦。
真实数据
对于真实场景,比如我们用手机拍摄了一组图像,怎么获得相机位姿?目前常用的方法是利用运动恢复结构(structure-from-motion, SFM)技术估计几个相机间的相对位姿。这个技术比较成熟了,现在学术界里用的比较多的开源软件包是COLMAP: https://colmap.github.io/。输入多张图像,COLMAP可以估计出相机的内参和外参(也就是sparse model)。
下面是COLMAP官网教程给的三个命令行操作步骤,简单来说: 第一步是对所有的图像进行特征点检测与提取,第二步是进行特征点匹配,第三步是进行SFM恢复相机位姿和稀疏的3D特征点。具体的使用方法和原理还请阅读其官方文档。其实COLMAP也集成了multiview stereo (MVS)算法用于重建场景完整的三维结构(也称为dense model)。不过NeRF本身是一种新颖的场景表征和重建算法,我们只需要相机的位姿信息,所以我们不需要跑MVS进行dense重建。注意:如果没有标定信息,基于单目的SFM无法获得场景的绝对尺度。
# The project folder must contain a folder "images" with all the images.
$ DATASET_PATH=/path/to/dataset
$ colmap feature_extractor \
--database_path $DATASET_PATH/database.db \
--image_path $DATASET_PATH/images
$ colmap exhaustive_matcher \
--database_path $DATASET_PATH/database.db
$ mkdir $DATASET_PATH/sparse
$ colmap mapper \
--database_path $DATASET_PATH/database.db \
--image_path $DATASET_PATH/images \
--output_path $DATASET_PATH/sparse使用COLMAP得到相机参数后只需要转成NeRF可以读取的格式即可以用于模型训练了。那这里面需要做什么操作?
LLFF真实数据格式
NeRF代码里用load_llff.py这个文件来读取真实的数据,第一次看到LLFF这个词可能不知道是什么意思。其实LLFF GitHub - Fyusion/LLFF: Code release for Local Light Field Fusion at SIGGRAPH 2019 是NeRF作者的上一篇做新视角合成的工作。为了和LLFF方法保持一致的数据格式,NeRF使用load_llff.py读取LLFF格式的真实数据,并建议大家使用LLFF提供的的imgs2poses.py文件获取所需相机参数。
COLMAP到LLFF数据格式
imgs2poses.py这个文件其实很简单,就干了两件事。
- 第一件事是调用colmap软件估计相机的参数,在sparse/0/文件夹下生成一些二进制文件:cameras.bin, images.bin, points3D.bin, project.ini。
- 第二件事是读取上一步得到的二进制文件,保存成一个poses_bounds.npy文件。
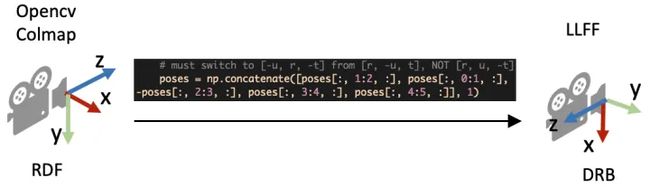
这里有一个细节需要注意,就是在pose_utils.py文件里load_colmap_data()函数的倒数第二行,有一个操作将colmap得到的c2w旋转矩阵中的第一列和第二列互换,第三列乘以负号:
# LLFF/llff/poses/pose_utils.py
def load_colmap_data(realdir):
...
# must switch to [-u, r, -t] from [r, -u, t], NOT [r, u, -t]
poses = np.concatenate([poses[:, 1:2, :], poses[:, 0:1, :], -poses[:, 2:3, :], poses[:, 3:4, :], poses[:, 4:5, :]], 1)
return poses, pts3d, perm还记得刚刚提到c2w旋转矩阵的三列向量分别代表XYZ轴的朝向,上述操作实际上就是把相机坐标系轴的朝向进行了变换:X和Y轴调换,Z轴取反,如下图所示:
从Colmap的坐标系转到LLFF的坐标系
poses_bounds.npy里有什么
load_llff.py会直接读取poses_bounds.npy文件获得相机参数。poses_bounds.npy是一个Nx17的矩阵,其中N是图像的数量,即每一张图像有17个参数。其中前面15个参数可以重排成3x5的矩阵形式:
poses_bounds.npy的前15维参数。左边3x3矩阵是c2w的旋转矩阵,第四列是c2w的平移向量,第五列分别是图像的高H、宽W和相机的焦距f
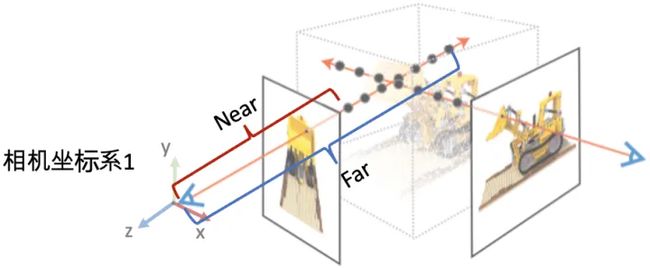
最后两个参数用于表示场景的范围Bounds (bds),是该相机视角下场景点离相机中心最近(near)和最远(far)的距离,所以near/far肯定是大于0的。
- 这两个值是怎么得到的?是在imgs2poses.py中,计算colmap重建的3D稀疏点在各个相机视角下最近和最远的距离得到的。
- 这两个值有什么用?之前提到体素渲染需要在一条射线上采样3D点,这就需要一个采样区间,而near和far就是定义了采样区间的最近点和最远点。贴近场景边界的near/far可以使采样点分布更加密集,从而有效地提升收敛速度和渲染质量。
poses_bounds.npy里最后两个参数(near/far)的作用示意图
load_llff.py代码解读
接着,我们介绍NeRF代码里load_llff.py代码里的一些细节。对三维视觉不熟悉的读者,早期读代码的时候可能会有不少困惑。
DRB到RUB的变换
第一个疑问是,为什么读进poses_bounds.npy里的c2w矩阵之后,对c2w的旋转矩阵又做了一些列变换?
# load_llff.py文件
def load_llff_data(basedir, factor=8, recenter=True, bd_factor=.75, spherify=False, path_zflat=False):
poses, bds, imgs = _load_data(basedir, factor=factor) # factor=8 downsamples original imgs by 8x
print('Loaded', basedir, bds.min(), bds.max())
# Correct rotation matrix ordering and move variable dim to axis 0
poses = np.concatenate([poses[:, 1:2, :], -poses[:, 0:1, :], poses[:, 2:, :]], 1)
...上面的代码段的最后一行实际上是把旋转矩阵的第一列(X轴)和第二列(Y轴)互换,并且对第二列(Y轴)做了一个反向。这样做的目的是将LLFF的相机坐标系变成OpenGL/NeRF的相机坐标系,如下图所示。
poses = np.concatenate([poses[:, 1:2, :], -poses[:, 0:1, :], poses[:, 2:, :]], 1)
缩放图像需要修改什么相机参数?
在_load_data()函数里,有一个用于图像缩放的factor比例参数,将HxW的图像缩放成(H/factor)x(W/factor)。这里面有一个问题是如果缩放了图像尺寸,相机的参数需要相应的做什么变化?
- 做法是:外参(位置和朝向)不变,相机的焦距f,cx, 和cy等比例缩放。下图的示意图展示了当相机位置不变,相机视野(Field of view, FOV)不变的情况下,图像的高和焦距长短的关系。
图像平面1与图像平面2拍摄的图像内容是一样的,只是分辨率不同
viewmatrix()
view_matrix是一个构造相机矩阵的的函数,输入是相机的Z轴朝向、up轴的朝向(即相机平面朝上的方向Y)、以及相机中心。输出下图所示的camera-to-world (c2w)矩阵。因为Z轴朝向,Y轴朝向,和相机中心都已经给定,所以只需求X轴的方向即可。又由于X轴同时和Z轴和Y轴垂直,我们可以用Y轴与Z轴的叉乘得到X轴方向。
camera-to-world matrix
下面是load_llff.py里关于view_matrix()的定义,看起来复杂一些。其实就是比刚刚的描述比多了一步:在用Y轴与Z轴叉乘得到X轴后,再次用Z轴与X轴叉乘得到新的Y轴。为什么这么做呢?这是因为传入的up(Y)轴是通过一些计算得到的,不一定和Z轴垂直,所以多这么一步。
# load_llff.py
def viewmatrix(z, up, pos):
vec2 = normalize(z)
vec1_avg = up
vec0 = normalize(np.cross(vec1_avg, vec2))
vec1 = normalize(np.cross(vec2, vec0))
m = np.stack([vec0, vec1, vec2, pos], 1)
return mposes_avg()
这个函数其实很简单,顾名思义就是多个相机的平均位姿(包括位置和朝向)。输入是多个相机的位姿。
- 第一步对多个相机的中心进行求均值得到center。
- 第二步对所有相机的Z轴求平均得到vec2向量(方向向量相加其实等效于平均方向向量)。
- 第三步对所有的相机的Y轴求平均得到up向量。
- 最后将vec2, up, 和center输入到刚刚介绍的viewmatrix()函数就可以得到平均的相机位姿了。
def poses_avg(poses):
hwf = poses[0, :3, -1:]
center = poses[:, :3, 3].mean(0)
vec2 = normalize(poses[:, :3, 2].sum(0))
up = poses[:, :3, 1].sum(0)
c2w = np.concatenate([viewmatrix(vec2, up, center), hwf], 1)
return c2w下图展示了一个poses_avg()函数的例子。左边是多个输入相机的位姿,右边是返回的平均相机姿态。可以看出平均相机位姿的位置和朝向是之前所有相机的均值。
中间大的坐标系是世界坐标系,每一个小的坐标系对应一个相机的局部坐标系。红绿蓝(RGB)轴分别代表XYZ轴
recenter_poses()
recenter_poses()函数的名字听起来是中心化相机位姿(同样包括位置和朝向)的意思。输入N个相机位姿,会返回N个相机位姿。
具体的操作了解起来可能有点跳跃。第一步先用刚刚介绍的poses_avg(poses)得到多个输入相机的平均位姿c2w,接着用这个平均位姿c2w的逆左乘到输入的相机位姿上就完成了归一化。
def recenter_poses(poses):
poses_ = poses+0
bottom = np.reshape([0,0,0,1.], [1,4])
c2w = poses_avg(poses)
c2w = np.concatenate([c2w[:3,:4], bottom], -2)
bottom = np.tile(np.reshape(bottom, [1,1,4]), [poses.shape[0],1,1])
poses = np.concatenate([poses[:,:3,:4], bottom], -2)
poses = np.linalg.inv(c2w) @ poses
poses_[:,:3,:4] = poses[:,:3,:4]
poses = poses_
return poses首先我们要知道利用同一个旋转平移变换矩阵左乘所有的相机位姿是对所有的相机位姿做一个全局的旋转平移变换,那下一个问题就是这些相机会被变到什么样的一个位置?我们可以用平均相机位姿作为支点理解,如果把平均位姿的逆c2w^-1左乘平均相机位姿c2w,返回的相机位姿中旋转矩阵为单位矩阵,平移量为零向量。也就是变换后的平均相机位姿的位置处在世界坐标系的原点,XYZ轴朝向和世界坐标系的向一致。
下图我们用一个例子帮助理解。左边和右边分别是输入和输出的相机位姿示意图。我们可以看到变换后的多个相机的平均位姿处在世界坐标系的原点,并且相机坐标系的XYZ轴与世界坐标系保持一致了。
中间大的坐标系是世界坐标系,每一个小的坐标系对应一个相机的局部坐标系。红绿蓝(RGB)轴分别代表XYZ轴
render_path_spiral()
这个函数写的有点复杂,它和模型训练没有关系,主要是用来生成一个相机轨迹用于新视角的合成,如下面视频所示:
00:04
下面只放了render_path_spiral()函数的定义,NeRF代码里还有一段是在准备输入参数,由于相关代码比较长就不贴出来。
def render_path_spiral(c2w, up, rads, focal, zdelta, zrate, rots, N):
render_poses = []
rads = np.array(list(rads) + [1.])
hwf = c2w[:,4:5]
for theta in np.linspace(0., 2. * np.pi * rots, N+1)[:-1]:
c = np.dot(c2w[:3,:4], np.array([np.cos(theta), -np.sin(theta), -np.sin(theta*zrate), 1.]) * rads)
z = normalize(c - np.dot(c2w[:3,:4], np.array([0,0,-focal, 1.])))
render_poses.append(np.concatenate([viewmatrix(z, up, c), hwf], 1))
return render_poses需要知道这个函数它是想生成一段螺旋式的相机轨迹,相机绕着一个轴旋转,其中相机始终注视着一个焦点,相机的up轴保持不变。简单说一下上面的代码:
首先是一个for循环,每一迭代生成一个新的相机位置。c是当前迭代的相机在世界坐标系的位置,np.dot(c2w[:3,:4], np.array([0,0,-focal, 1.])是焦点在世界坐标系的位置,z是相机z轴在世界坐标系的朝向。接着使用介绍的viewmatrix(z, up, c)构造当前相机的矩阵。
下面这个图可视化了 render_path_spiral()生成的轨迹。
中间大的坐标系是世界坐标系,每一个小的坐标系对应一个相机的局部坐标系。红绿蓝(RGB)轴分别代表XYZ轴
spherify_poses()
刚刚介绍的render_path_spiral()假设所有相机都朝向某一个方向,也就是所谓的faceforward场景。对于相机围绕着一个物体拍摄的360度场景,NeRF代码提供了一个spherify_poses()的函数用于"球面化"相机分布并返回一个环绕的相机轨迹用于新视角合成。这里插一句,在训练360度场景的时候,需要配合"--no_ndc --spherify --lindisp"三个参数以得到好的结果,具体原理这里不展开介绍。
if spherify:
poses, render_poses, bds = spherify_poses(poses, bds)这个函数也比较复杂,前半部分是在将输入的相机参数进行归一化,后半部分是生成一段相机轨迹用于合成新视角。对输入相机参数进行归一化时,思路是:
- 用 pt_mindist = min_line_dist(rays_o, rays_d)找到离所有相机中心射线距离之和最短的点(可以先简单理解成场景的中心位置)
rays_d = poses[:,:3,2:3]
rays_o = poses[:,:3,3:4]
def min_line_dist(rays_o, rays_d):
A_i = np.eye(3) - rays_d * np.transpose(rays_d, [0,2,1])
b_i = -A_i @ rays_o
pt_mindist = np.squeeze(-np.linalg.inv((np.transpose(A_i, [0,2,1]) @ A_i).mean(0)) @ (b_i).mean(0))
return pt_mindist
pt_mindist = min_line_dist(rays_o, rays_d)- 将得到的场景中心位置移到世界坐标系的原点,同时将所有相机z轴的平均方向转到和世界坐标系的z轴相同
center = pt_mindist
up = (poses[:,:3,3] - center).mean(0)
vec0 = normalize(up)
vec1 = normalize(np.cross([.1,.2,.3], vec0))
vec2 = normalize(np.cross(vec0, vec1))
pos = center
c2w = np.stack([vec1, vec2, vec0, pos], 1)
poses_reset = np.linalg.inv(p34_to_44(c2w[None])) @ p34_to_44(poses[:,:3,:4])- 最后将相机的位置缩放到单位圆内
rad = np.sqrt(np.mean(np.sum(np.square(poses_reset[:,:3,3]), -1)))
sc = 1./rad
poses_reset[:,:3,3] *= sc下面这个图可视化了spherify_poses()返回的结果。
中间大的坐标系是世界坐标系,每一个小的坐标系对应一个相机的局部坐标系。红绿蓝(RGB)轴分别代表XYZ轴
3D空间射线怎么构造
最后我们看一下这个射线是怎么构造的。给定一张图像的一个像素点,我们的目标是构造以相机中心为起始点,经过相机中心和像素点的射线。
首先,明确两件事:
- 一条射线包括一个起始点和一个方向,起点的话就是相机中心。对于射线方向,我们都知道两点确定一条直线,所以除了相机中心我们还需另一个点,而这个点就是成像平面的像素点。
- NeRF代码是在相机坐标系下构建射线,然后再通过camera-to-world (c2w)矩阵将射线变换到世界坐标系。
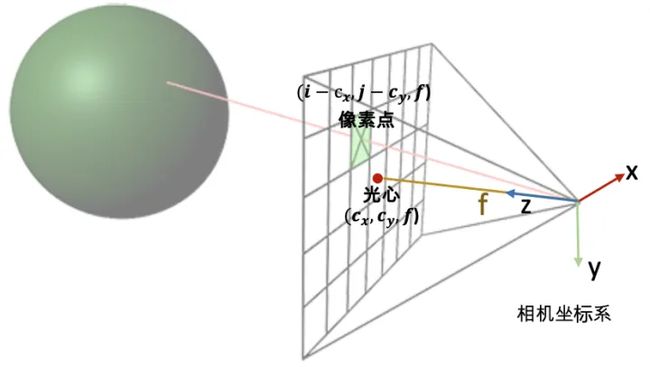
通过上述的讨论,我们第一步是要先写出相机中心和像素点在相机坐标系的3D坐标。下面我们以OpenCV/Colmap的相机坐标系为例介绍。相机中心的坐标很明显就是[0,0,0]了。像素点的坐标可能复杂一点:首先3D像素点的x和y坐标是2D的图像坐标 (i, j)减去光心坐标 (cx,cy),然后z坐标其实就是焦距f (因为图像平面距离相机中心的距离就是焦距f)。
所以我们就可以得到射线的方向向量是 (�−��,�−��,�)−(0,0,0)=(�−��,�−��,�) 。因为是向量,我们可以把整个向量除以焦距f归一化z坐标,得到 (�−���,�−���,1) 。
接着只需要用c2w矩阵把相机坐标系下的相机中心和射线方向变换到世界坐标系就搞定了。
OpenCV/Colmap相机坐标系下射线的构造示意图
下面是NeRF的实现代码。但关于这里面有一个细节需要注意一下:为什么函数的第二行中dirs的y和z的方向值需要乘以负号,和我们刚刚推导的的 (�−���,�−���,1) 不太一样呢?
def get_rays_np(H, W, K, c2w):
i, j = np.meshgrid(np.arange(W, dtype=np.float32), np.arange(H, dtype=np.float32), indexing='xy')
dirs = np.stack([(i-K[0][2])/K[0][0], -(j-K[1][2])/K[1][1], -np.ones_like(i)], -1)
# Rotate ray directions from camera frame to the world frame
rays_d = np.sum(dirs[..., np.newaxis, :] * c2w[:3,:3], -1) # dot product, equals to: [c2w.dot(dir) for dir in dirs]
# Translate camera frame's origin to the world frame. It is the origin of all rays.
rays_o = np.broadcast_to(c2w[:3,-1], np.shape(rays_d))
return rays_o, rays_d这是因为OpenCV/Colmap的相机坐标系里相机的Up/Y朝下, 相机光心朝向+Z轴,而NeRF/OpenGL相机坐标系里相机的Up/朝上,相机光心朝向-Z轴,所以这里代码在方向向量dir的第二和第三项乘了个负号。
参考网址:
https://zhuanlan.zhihu.com/p/593204605/
更多阅读材料:
前面简单地介绍了下NeRF代码中关于相机参数和坐标系变换的内容,这里面有很多细节没有展开介绍,如果有错误还请批评指正。另外,如果初学者希望进一步学习3D、图形学渲染相关的知识,可以浏览下面的一些网站(不全面,仅供参考):
- Scratchapixel系列:https://www.scratchapixel.com/
- 很棒的一个网站,这个网站里介绍了很多关于计算机图形学渲染的知识。可以从头开始学习或者直接先看 Computing the Pixel Coordinates of a 3D Point
- The Perspective Camera - An Interactive Tour:https://ksimek.github.io/2012/08/13/introduction/
- 这个网站介绍了相机的内外参数和分解,Dissecting the Camera Matrix part1/part2/part3
- 一篇很详细的关于体素渲染和NDC空间的博客:A Surge in NeRF | Will
下面是关于NeRF研究方向的一些文章(不全面,仅供参考):
- Frank Dellaert-NeRF Explosion 2020
- Frank Dellaert-NeRF at ICCV 2021
- NeRF at CVPR 2022
- 每周分类神经辐射场: https://github.com/sjtuytc/LargeScaleNeRFPytorch/blob/main/docs/weekly_nerf_cn.mdc