二维数组创建方式比较
暑假跟着地质队去跑山了，到现在还没结束，今天休息的时候突然刷到了一篇关于C++二维数组创建方面的文章，我觉得还是非常不错滴，就将其中提到的新方法和我已经使用过的三种方法进行了比较，发现该方法提高了二维数组的分配、访存和运算速度，我用了四种方法：1、常规动态二维数组声明、2、新方法动态二维数组声明、3、Vector容器创建方式1、4、Vector容器创建方式2。
测试数组大小都是20000*20000，这里只展示了其中的5*5的切片，我会先讲各种方法的原理，最后展示各方法的运行时长。
四个函数的功能都是计算直角三角形斜边长。
目录
1、常规动态二维数组声明
2、新方法动态二维数组声明
3、Vector容器声明方法一
4、Vector容器创建方法二
5、绘图解释
6、对比结果
7、程序代码
1、常规动态二维数组声明
这个方式就是最简单也是最常用的方式，先说明一个一维的指针数组，然后每个指针在指向一个数组的地址，就行了，访存则是先找到A[i][j]所对应的指针A[i]，再找A[i][j]就行，更通俗的理解就是，这种逐行分配的方法会使得上一行和下一行的地址是不连续的，寻址效率会降低，这里给出代码：
void originalDynamic(int n){
clock_t start = clock();
double** a = new double* [n];
double** b = new double* [n];
double** c = new double* [n];
for (int i = 0; i < n; i++) {
a[i] = new double[n]();
b[i] = new double[n]();
c[i] = new double[n]();
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
a[i][j] = 3.0;
b[i][j] = 4.0;
c[i][j] = 0.0;
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
c[i][j] = sqrt(powl(a[i][j],2) + powl(b[i][j],2));
}
}
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
cout << c[i][j] << '\t';
}
cout << endl;
}
clock_t end = clock();
cout << " Original time:" << (end - start)/CLOCKS_PER_SEC << endl;
}2、新方法动态二维数组声明
出现这个方法的原因是这样的，方法一的地址实际上是不连续的，也就是说访存过程会浪费额外时间，通过将数组地址连续化，就可以节省访存时间，进而提高访存效率。
先贴代码：
void newDynamic(int n){
clock_t start = clock();
double** a = new double* [n];
double** b = new double* [n];
double** c = new double* [n];
a[0] = new double[n * n];
b[0] = new double[n * n];
c[0] = new double[n * n];
for (int i = 1; i < n; i++) {
a[i] = a[0] + i * n;
b[i] = b[0] + i * n;
c[i] = c[0] + i * n;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
a[i][j] = 3.0;
b[i][j] = 4.0;
c[i][j] = 0.0;
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
c[i][j] = sqrt(powl(a[i][j], 2) + powl(b[i][j], 2));
}
}
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
cout << c[i][j] << '\t';
}
cout << endl;
}
clock_t end = clock();
cout << "New time:" << (end - start)/CLOCKS_PER_SEC << endl;
}只需要看6-13行就行，可以看到再第一行的首地址申请空间的时候就把整个二维数组的空间全部申请了，再把其余隔行都依次对应到首地址之后的地址，这样就使得整个数组的地址连续化，从而提高了访存效率。咋说呢，我觉得这个有点像C++中一维数组变二维数组，看代码的逻辑上也很像：
//一维数组做二维数组使用：
double *array1=new double[n*n];
//二维数组的下标对应方式就是：
array[i][j]=array1[i*row+j];上述的这个方式我之前用CUDA做东西的时候用的很多，今天这个二维数组声明方法实际上就是上述的一维数组做二维数组方法的变形。
3、Vector容器声明方法一
个人觉得这个方法是Vector数组声明方法中最简单的，也是最高效的一种，这里就不讲什么原理了，会使用就好：
void usingVectorway1(int n){
clock_t start = clock();
vector>a(n, vector(n, 3.0));
vector>b(n, vector(n, 4.0));
vector>c(n, vector(n, 0.0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
c[i][j] = sqrt(powl(a[i][j], 2) + powl(b[i][j], 2));
}
}
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
cout << c[i][j] << '\t';
}
cout << endl;
}
clock_t end = clock();
cout << "vector Way1 time:" << (end - start)/CLOCKS_PER_SEC<< endl;
} 直接按照3-5行的声明方式声明，容器类就会给你创建好。
4、Vector容器创建方法二
这个方法是一种笨办法，最慢也最不推荐使用，但是还是可以作为一个反例来给出：
但这个方法是最好理解的：先创建一个大小为n的vector数组，然后每个都resize成一个大小为n的一维数组，再遍历，赋值，特别麻烦，和第一种有着异曲同工之妙，但是也是最慢的。
void usingVectorway2(int n){
clock_t start = clock();
vector> a(n);
vector> b(n);
vector> c(n);
for (int i = 0; i < n; i++) {
a[i].resize(n);
b[i].resize(n);
c[i].resize(n);
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
a[i][j]=3.0;
b[i][j]=4.0;
c[i][j]=1.0;
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
c[i][j] = sqrt(powl(a[i][j], 2) + powl(b[i][j], 2));
}
}
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
cout << c[i][j] << '\t';
}
cout << endl;
}
clock_t end = clock();
cout << "Vector Way2 time:" << (end - start)/CLOCKS_PER_SEC << endl;
} 5、绘图解释
第一种和第四种方法原理是这样的：
标题方法一和方法四
第二种方法：
方法二
这下就很清楚了。
6、对比结果
最后我们来看看这四种方法的运行结果，主要是看他们的运行时长：
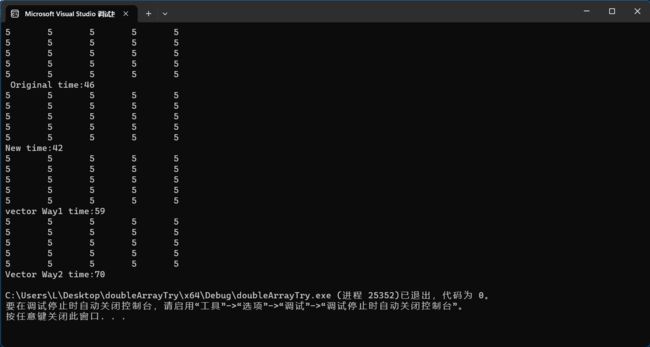运行时长对比
可以看出，新方法（方法二）的速度最快，而方法四的速度最慢，这说明我们改变声明和访存方式之后，分配、访存、计算速度是有所提升的，新方法是行之有效的。
7、程序代码
这里贴上所有程序代码，不写注释了，上面各函数都讲了：
#include
#include
#include
using namespace std;
void originalDynamic(int n);
void newDynamic(int n);
void usingVectorway1(int n);
void usingVectorway2(int n);
int main() {
const int n = 20000;
originalDynamic(n);
newDynamic(n);
usingVectorway1(n);
usingVectorway2(n);
}
void originalDynamic(int n){
clock_t start = clock();
double** a = new double* [n];
double** b = new double* [n];
double** c = new double* [n];
for (int i = 0; i < n; i++) {
a[i] = new double[n]();
b[i] = new double[n]();
c[i] = new double[n]();
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
a[i][j] = 3.0;
b[i][j] = 4.0;
c[i][j] = 0.0;
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
c[i][j] = sqrt(powl(a[i][j],2) + powl(b[i][j],2));
}
}
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
cout << c[i][j] << '\t';
}
cout << endl;
}
clock_t end = clock();
cout << " Original time:" << (end - start)/CLOCKS_PER_SEC << endl;
}
void newDynamic(int n){
clock_t start = clock();
double** a = new double* [n];
double** b = new double* [n];
double** c = new double* [n];
a[0] = new double[n * n];
b[0] = new double[n * n];
c[0] = new double[n * n];
for (int i = 1; i < n; i++) {
a[i] = a[0] + i * n;
b[i] = b[0] + i * n;
c[i] = c[0] + i * n;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
a[i][j] = 3.0;
b[i][j] = 4.0;
c[i][j] = 0.0;
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
c[i][j] = sqrt(powl(a[i][j], 2) + powl(b[i][j], 2));
}
}
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
cout << c[i][j] << '\t';
}
cout << endl;
}
clock_t end = clock();
cout << "New time:" << (end - start)/CLOCKS_PER_SEC << endl;
}
void usingVectorway1(int n){
clock_t start = clock();
vector>a(n, vector(n, 3.0));
vector>b(n, vector(n, 4.0));
vector>c(n, vector(n, 0.0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
c[i][j] = sqrt(powl(a[i][j], 2) + powl(b[i][j], 2));
}
}
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
cout << c[i][j] << '\t';
}
cout << endl;
}
clock_t end = clock();
cout << "vector Way1 time:" << (end - start)/CLOCKS_PER_SEC<< endl;
}
void usingVectorway2(int n){
clock_t start = clock();
vector> a(n);
vector> b(n);
vector> c(n);
for (int i = 0; i < n; i++) {
a[i].resize(n);
b[i].resize(n);
c[i].resize(n);
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
a[i][j]=3.0;
b[i][j]=4.0;
c[i][j]=1.0;
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
c[i][j] = sqrt(powl(a[i][j], 2) + powl(b[i][j], 2));
}
}
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
cout << c[i][j] << '\t';
}
cout << endl;
}
clock_t end = clock();
cout << "Vector Way2 time:" << (end - start)/CLOCKS_PER_SEC << endl;
}
ok，学到一种新方法还是很高兴的。