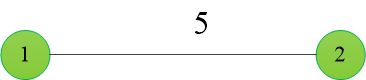数据结构与算法--图

 

1 图的基本概念

 

图(Graph) 是由一个顶点集V和一个弧集E构成的网状数据结构，记作 $G=(V,E)$ 在图中，数据元素通常称作顶点(Vertex)，V是顶点的有穷非空集合；VR是两个顶点之间的关系的集合

线性表可以为空表,树可以是空树,但是图不可以为空,即图一定是非空集

align= right>

---

 

2 无向图和有向图

 

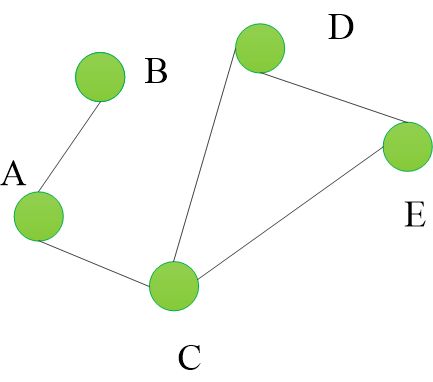
在一个图中，如果任意两个顶点构成的偶对(a,b)属于E是无序的,即顶点之间的连线是没有方向的,则称该图为无向图。

在一个图中，如果任意两个顶点构成的偶对(a,b)属于E是有序的,即顶点之间的连线是有方向的,则称为有向图

---

 

3 图相关的关键术语

 

顶点 :  图中的节点

弧 :   有向图 v为起点 w为终点 表示v到w的一条弧

边 :    无向图 有就有

权 :   可以理解成边的长度

顶点的度 :    和该顶点相关联的边的数目 度 = 入度 + 出度

顶点的入度 :   该顶点为终点

顶点的出度 :   该顶点为起点

路径 :    从一个顶点到另一个顶点的路径

连通图 :    任意两个顶点都是连通的

---

 

4 图的相关性质

 
设 n为图中的节点数
e为边或弧的数目 则有如下性质

1. 在无向图中
   e的取值范围是 0 ~ n(n-1)/2
   在无向图中,如果有e = n(n-1)/2,则为完全图
    

2. 在有向图中
   e的取值范围是 n(n-1)
   在有向图中，如有n(n-1)条弧，则称为有向完全图

---

 

5 图的存储

 

邻接表法 邻接矩阵法

图

4.1 邻接表法

 
使用链表来表示图的连接关系,对于每个顶点,使用链表存储与其相邻的顶点,邻接表的优点是对于稀疏图而言,存储空间较小;同时可以快速遍历每一个顶点的邻接顶点,但是查找两个顶点之间是否存在边的时间复杂度为 $O(k)$,其中k是相邻顶点的数量

特点 :

1. 在邻接表中，给定一顶点就很容易地找到它所有邻边

2. 在有向图的邻接表中，求一个给定顶点的出度只需计算其邻接表中的结点个数即可，但求某顶点的入度，则需要遍历全部的邻接表

3. 图的邻接表表示并不唯一，因为各边表结点的顺序是任意的

4. 邻接表便于增加和删除节点，便于统计边数

邻接表属于链式存储，但邻接表的表头属于顺序存储结构

4.2 邻接矩阵法

使用一个二维数组来表示图的连接关系,对于n个顶点的无向图,使用 n * n的矩阵表示 如果两个顶点 i和j之间存在边,则在矩阵中 (i,j) 和 (j,i)的值为1,否则为0,(i,j) 位置的值表示从顶点i到顶点j的边

邻接矩阵的优势是查找两个顶点之间是否存在边的时间复杂度为 $O(n)$

无向图的邻接矩阵一定是对称矩阵

---

 

6 图的代码表示

 
顶点

public class Node {
    // 点上的值
    public int value;
    // 一个点的入度 有多少条边指向自己
    public int in;
    // 一个点的出度 一个点指向其它点的边个数
    public int out;

    // 从自己出发直接相邻的点
    public ArrayList<Node> nexts;
    // 属于这个节点的边有哪些
    public ArrayList<Edge> edges;

    public Node(int value){
        this.value = value;
        in = 0;
        out = 0;
        nexts = new ArrayList<>();
        edges = new ArrayList<>();
    }
}

边

public class Edge {
    public int weight;// 权值可以表示距离
    public Node from;// 
    public Node to;// 

    public Edge(int weight, Node from, Node to) {
        this.weight = weight;
        this.from = from;
        this.to = to;
    }
}

图

/**
 * 图的表示方式 邻接图 邻接矩阵
 * @author Mrchao
 * @version 1.0.0
 * @date 2023-07-10
 */
public class Graph {
    // 点集 key 点的编号 Node实际的点
    public HashMap<Integer,Node> nodes;
    // 边集
    public HashSet<Edge> edges;

    public Graph(){
        nodes = new HashMap<>();
        edges = new HashSet<>();
    }
}

---

 

7 图的构建

 

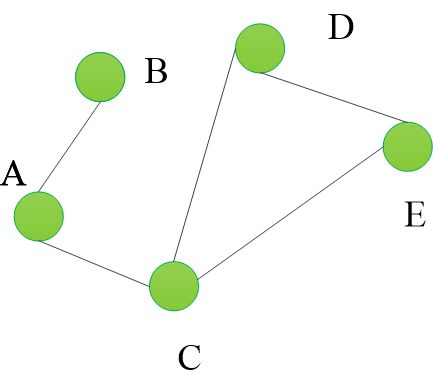
假如有一个N * 3的数组,用于表示一个城市到另一个城市的距离,第一列表示出发城市,第二列表示到达城市,第三列表示两个城市的距离,如图所示

表示1号城市到2号城市的距离为5,如果有多个这样的数据,如何构建一张图

例如要构建如图所示的图:

public static void main(String[] args) {
    int[][] cityMatrix = new int[][]{
            {1,2,10},
            {2,3,8},
            {3,4,7},
            {4,5,9},
            {5,3,4}
    };
    createGraph(cityMatrix);
}

/**
 * matrix[i][0] 起始城市
 * matrix[i][1] 终止城市
 * matrix[i][2] 两个城市之间的距离
 *
 * @param matrix
 * @return
 */
public static Graph createGraph(int[][] matrix) {
    Graph graph = new Graph();
    for (int i = 0; i < matrix.length;++i){
        // 起始城市的编号
        int from = matrix[i][0];
        // 终止城市的编号
        int to = matrix[i][1];
        // 两个城市之间的距离
        int weight = matrix[i][2];

        // 如果图中没有包含这两个城市,则将这两个城市当做点加入到图中
        if (!graph.nodes.containsKey(from)){
            // key点的编号 value实际的点
            graph.nodes.put(from,new Node(from));
        }

        if (!graph.nodes.containsKey(to)){
            graph.nodes.put(to,new Node(to));
        }

        Node fromNode = graph.nodes.get(from);
        Node toNode = graph.nodes.get(to);
        // 创建边
        Edge edge = new Edge(weight,fromNode,toNode);
        // 起始城市的邻居是toNode
        fromNode.nexts.add(toNode);
        // 起始城市的边
        fromNode.edges.add(edge);
        // 终止城市的边
        toNode.edges.add(edge);
        // 起始城市的出度+1
        fromNode.out++;
        //终止城市的入度+1
        toNode.in++;
        // 边加入图中
        graph.edges.add(edge);
    }
    return graph;
}

---

 

8 图的宽度优先遍历

 

利用队列实现

1. 从源节点开始,依次按照宽度进队列,然后弹出
2. 每次弹出一个节点,把该节点所有没有进过队列的邻接节点放入队列
3. 直到队列为空

 /**
   * 从源节点出发进行宽度优先遍历
   * @param node
   */
  public static void broadFirstTraversal(Node node){
      if (node == null){
          return;
      }
      Queue<Node> queue = new LinkedList<>();
      // 为了保证放入队列的节点不重复
      HashSet<Node> set = new HashSet<>();
      
      queue.add(node);
      set.add(node);
      while (!queue.isEmpty()){
          Node cur = queue.poll();
          System.out.println(cur.val);
          //遍历当前点的所有邻接节点
          for (Node next : cur.nexts) {
              if (!set.contains(next)){
                  queue.add(next);
                  set.add(next);
              }
          }
      }
  }

---

 

9 图的广度优先遍历

 

1. 利用栈实现
2. 从源节点开始把节点按照深度放入栈,然后弹出
3. 每次弹出一个节点,把该节点所有没有进过栈的邻节点放入栈
4. 直到栈变空

public class DFSTest {
    public static void main(String[] args) {
        int[][] cityMatrix = new int[][]{
                {1,2,10},
                {2,3,8},
                {3,4,7},
                {4,5,9},
                {5,3,4},
                {1,3,20},
                {1,5,70}
        };
        Graph graph = CreGraphTest.createGraph(cityMatrix);
        depthFirstTraversal(graph.nodes.get(1));
    }

    /**
     *
     * @param node 图中的源节点
     */
    public static void depthFirstTraversal(Node node){
        if (node == null){
            return;
        }
        // 深度优先遍历 使用栈
        Stack<Node> stack = new Stack<>();
        HashSet<Node> set = new HashSet<>();
        stack.push(node);
        set.add(node);
        System.out.println(node.val);
        while (!stack.isEmpty()){
            Node cur = stack.pop();
            for (Node next : cur.nexts) {
                // 没有遍历过将cur压入到栈中
                if (!set.contains(next)){
                    // 栈中存放的是每次按深度优先遍历的顶点
                    stack.push(cur);
                    stack.push(next);
                    set.add(next);
                    System.out.println(next.val);
                    break;
                }
            }
        }
    }
}

---

 

10 拓扑排序算法

 

要求 : 有向图,且有入度为0的节点,且没有环

比如在编译一个模板时,有如下依赖关系
 

要得到A包,编译顺序如下 :

E–>D–>D–>B–>A

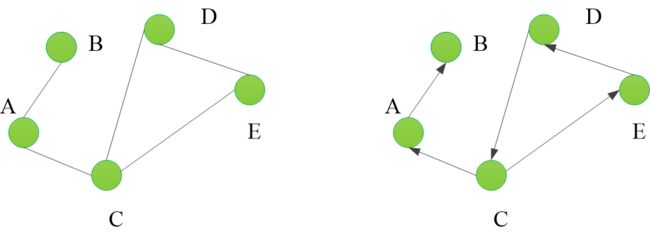
在比如如下的图:
 

 

依次找到入度为0的点,擦掉它的影响

public class TopologySortTest {
    public static void main(String[] args) {
        Integer[][] matrix = new Integer[][]{
                {1,2,0},
                {1,3,0},
                {2,3,0},
                {2,4,0},
                {3,4,0},
                {4,5,0}
        };
        Graph graph = GraphGene.createGraph(matrix);
        List<Node> nodes = topologySort(graph);
        for(Node node :nodes){
            System.out.print(node.value + " ");
        }
        System.out.println();
    }

    public static List<Node> topologySort(Graph graph){
        Map<Node,Integer> inMap = new HashMap<>();// key图中的某个节点 value 剩余的入度
        // 只有入度为0的点 才能进这个队列
        Queue<Node> zeroInQueue = new LinkedList<>();
        //遍历图中的每一个顶点 遇到入度为0的顶点则放入到0入度队里
        for (Node node : graph.nodes.values()) {
            inMap.put(node,node.in);
            if(node.in == 0){
                zeroInQueue.add(node);
            }
        }
        // 拓扑排序的结果
        List<Node> retList = new ArrayList<>();
        while (!zeroInQueue.isEmpty()){
            Node cur = zeroInQueue.poll();
            retList.add(cur);
            // 遍历此顶点所有的邻接节点
            for (Node next : cur.nexts){
                // 将邻接节点的入度减 1
                inMap.put(next,inMap.get(next) - 1);
                // 入度为 0 则加入0入度队列
                if (inMap.get(next) == 0){
                    zeroInQueue.add(next);
                }
            }
        }
        return retList;
    }
}

---

 

11 kruskal算法(从边出发)

 

适用范围 : 要求无向图

生成最小生成树,保证连通,连通之后所有边的权值之和是最小的

从图的最小的边开始,依次加入,如果不会形成环,则加入,否则不加入

如何在加入边的时候,判断是否会形成环,使用并查集

集合的查询和集合的合并,使用并查集

public class KruskalTest {
    public static class MySets {
        // key 每个点 value每个点对应的集合
        public HashMap<Node, List<Node>> setMap = new HashMap<>();

        public MySets(List<Node> nodes) {
            for (Node cur : nodes) {
                // 最开始 所有的点所在的集合只有自己
                List<Node> set = new ArrayList<>();
                set.add(cur);
                setMap.put(cur, set);
            }
        }

        /**
         * 判断 from点和to点是否在同一个集合里
         *
         * @param from
         * @param to
         * @return
         */
        public boolean isSameSet(Node from, Node to) {
            List<Node> fromSet = setMap.get(from);
            List<Node> toSet = setMap.get(to);
            // 直接比较内存地址是否一致
            return fromSet == toSet;
        }

        /**
         * from节点所在的集合和to所在的集合合并
         *
         * @param from
         * @param to
         */
        public void union(Node from, Node to) {
            List<Node> fromSet = setMap.get(from);
            List<Node> toSet = setMap.get(to);

            // 把to集合中的元素加入到from中
            for (Node toNode : toSet) {
                fromSet.add(toNode);
                setMap.put(toNode, fromSet);
            }
        }
    }

    public static class EdgeComparator implements Comparator<Edge> {
        @Override
        public int compare(Edge o1, Edge o2) {
            return o1.weight - o2.weight;
        }
    }


    /**
     * 生成最小生成树
     *
     * @param graph
     * @return
     */
    public static Set<Edge> kruskalMST(Graph graph) {
        List<Node> nodeList = new ArrayList<>();
        nodeList.addAll(graph.nodes.values());
        MySets mySets = new MySets(nodeList);

        PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
        // 把图中所有的边加入到队列中
        for (Edge edge : graph.edges) {
            priorityQueue.add(edge);
        }

        Set<Edge> retSet = new HashSet<>();

        while (!priorityQueue.isEmpty()) {
            Edge edge = priorityQueue.poll();
            // 判断当前边的from点和to点是否在一个集合里
            if (!mySets.isSameSet(edge.from, edge.to)) {
                retSet.add(edge);
                // 合并当前边的顶点
                mySets.union(edge.from, edge.to);
            }
        }
        return retSet;
    }
}

---

 

12 prime 算法(从点出发)

 
适用于无向图
 

 

1. 从图中选择一个起始节点,如果没有被处理过,则将该节点加入到已处理的集合中

2. 遍历此节点所有的边,加入到优先级队里(优先级队里按边的权值大小排序)

3. 从优先级队列中弹出一条边,找到此条边的to节点,如果to节点未处理过,则将to节点加入到已处理过的节点中,此条边加入到结果集中,遍历图节点的所有邻边,加入到优先级队列,循环往复,直到队里为空

public class PrimeMSTTest {

    public static class EdgeComparator implements Comparator<Edge> {

        @Override
        public int compare(Edge o1, Edge o2) {
            return o1.weight - o2.weight;
        }
    }

    /**
     * 从边出发 生成最小生成树
     *
     * @param graph
     * @return
     */
    public static Set<Edge> primMST(Graph graph) {
        Set<Edge> retSet = new HashSet<>();
        if (graph == null) {
            return retSet;
        }
        // 存放点解锁的边
        PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
        // 存放已经考察过的点
        Set<Node> nodeSet = new HashSet<>();
        // 从任意一个点出发
        for (Node node : graph.nodes.values()) {
            if (!nodeSet.contains(node)) {
                nodeSet.add(node);
                // 把该点解锁的边加入到队列
                for (Edge edge : node.edges) {
                    priorityQueue.add(edge);
                }
                while (!priorityQueue.isEmpty()) {
                    Edge edge = priorityQueue.poll();
                    Node toNode = edge.to;
                    if (!nodeSet.contains(toNode)) {
                        // 被解锁边的节点被考察过
                        nodeSet.add(toNode);
                        retSet.add(edge);
                        for (Edge nextEdge : toNode.edges) {
                            priorityQueue.add(nextEdge);
                        }
                    }
                }
            }
        }
        return retSet;
    }
}

---

 

13 dijkstras算法

 

适用范围 : 不能有累加和为负数的环

单元最短路径算法

规定一个出发点,到后续每一个点最短距离是多少

整体步骤 :

1. 创建一张Hash表,存放处理过程中到给定节点最短的距离,创建一个 Set存放已经 被处理过的节点

2. 从Hash表中找到一个未被处理过的距离给定节点最短的节点

3. 遍历2中得到的节点所有的边,处理该点到每条边的 toNode 的距离

4. 循环整个过程

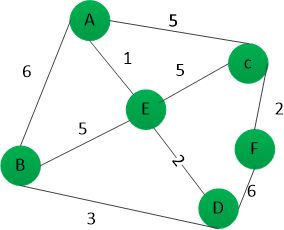
比如处理如图所示的图

代码如下 :

public class DijkstraTest {
    public static void main(String[] args) {
        Integer[][] graphArr = new Integer[][]
                {
                        {1, 2, 3},
                        {1, 3, 15},
                        {1, 4, 8},
                        {2, 3, 2},
                        {2, 5, 7},
                        {3, 4, 900},
                        {3, 5, 3},
                        {4, 5, 10}
                };
        Graph graph = GraphGene.createGraph(graphArr);
        Node node = graph.nodes.get(1);
        Map<Node, Integer> nodeIntegerMap = dijkstra(node);
        for (Map.Entry<Node, Integer> entry : nodeIntegerMap.entrySet()) {
            System.out.println("node : " + entry.getKey().value + " is " + entry.getValue());
        }
    }
    public static Map<Node, Integer> dijkstra(Node head) {
        // key 图中的每一个节点
        // value  给定的节点到 图中每个节点的最小距离
        Map<Node, Integer> distanceMap = new HashMap<>();
        distanceMap.put(head, 0);
        Set<Node> selectNodes = new HashSet<>();
        Node node = getMinDistanceAndUnselectedNode(distanceMap, selectNodes);
        while (node != null) {
            for (Edge edge : node.edges) {
                Node toNode = edge.to;
                //该点的边没有被处理,则更新
                if (!distanceMap.containsKey(toNode)) {
                    distanceMap.put(toNode, distanceMap.get(node) + edge.weight);
                }
                // 距离谁小 就取谁
                distanceMap.put(toNode, Math.min(distanceMap.get(toNode),
                        distanceMap.get(node) + edge.weight));
            }
            selectNodes.add(node);
            node = getMinDistanceAndUnselectedNode(distanceMap, selectNodes);
        }
        return distanceMap;
    }


    /**
     * 从 distanceMap 选择一个距离最小的没有被考察过的节点
     *
     * @param distanceMap
     * @param touchedNode
     * @return
     */
    public static Node getMinDistanceAndUnselectedNode(Map<Node, Integer> distanceMap,
                                                       Set<Node> touchedNode) {
        Integer minDistance = Integer.MAX_VALUE;
        Node minNode = null;
        Set<Map.Entry<Node, Integer>> entrySet = distanceMap.entrySet();
        for (Map.Entry<Node, Integer> entry : entrySet) {
            Node node = entry.getKey();
            Integer distance = entry.getValue();
            if (!touchedNode.contains(node) && distance < minDistance) {
                minDistance = distance;
                minNode = node;
            }
        }
        return minNode;
    }
}