Rstudio做多元统计分析R语言
练习题4
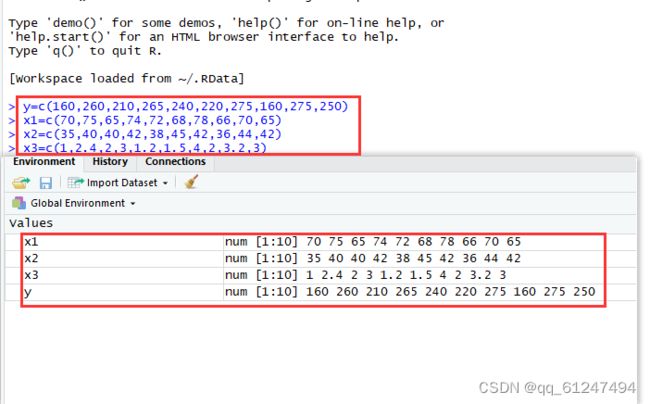
研究货运总量y（万吨）与工业总产值x1（亿元）、农业总产值x2（亿元）、居民非商品支出x3（亿元）的关系。数据见表4-8.
表4-8
| 编号 |
y |
X1 |
X2 |
X3 |
| 1 |
160 |
70 |
35 |
1 |
| 2 |
260 |
75 |
40 |
2.4 |
| 3 |
210 |
65 |
40 |
2 |
| 4 |
265 |
74 |
42 |
3 |
| 5 |
240 |
72 |
38 |
1.2 |
| 6 |
220 |
68 |
45 |
1.5 |
| 7 |
275 |
78 |
42 |
4 |
| 8 |
160 |
66 |
36 |
2 |
| 9 |
275 |
70 |
44 |
3.2 |
| 10 |
250 |
65 |
42 |
3 |
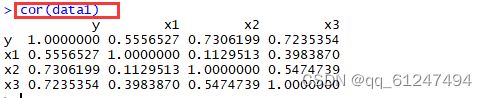
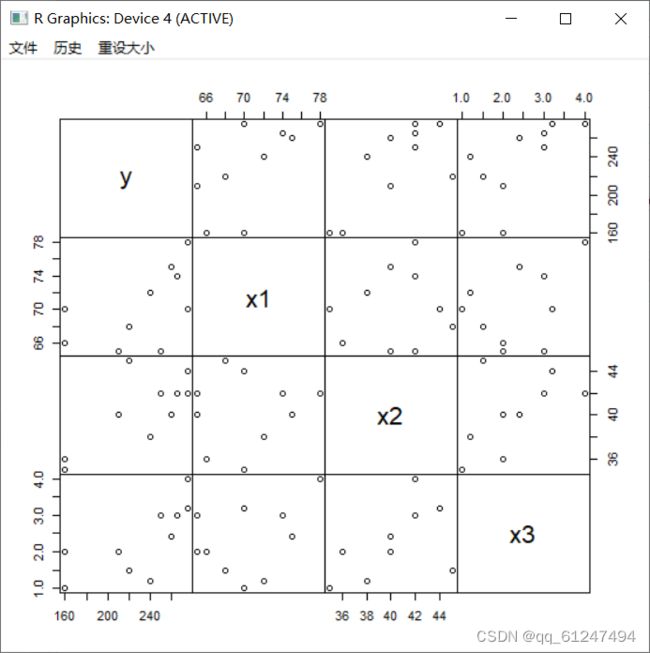
- 计算出y，x1，x2，x3的相关系数矩阵并绘制矩阵散点图。
（2）求出y与x1，x2，x3的三元线性回归方程。
（3）对所求的方程做拟合优度检验。
（4）对回归方程做显著性检验，对每一个回归系数做显著性检验。
（5）如果有的回归系数没有通过显著性检验，将其剔除，重新建立回归方程；并做回归方程的显著性检验和回归系数的显著性检验。
（6）使用逐步回归分析的逐步筛选方法获得一个最优的回归模型.
解：
- 计算出y，x1，x2，x3的相关系数矩阵。
①用函数C创建向量y,x1,x2,x3向量
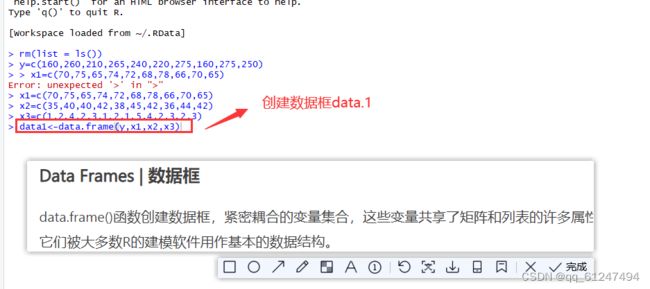
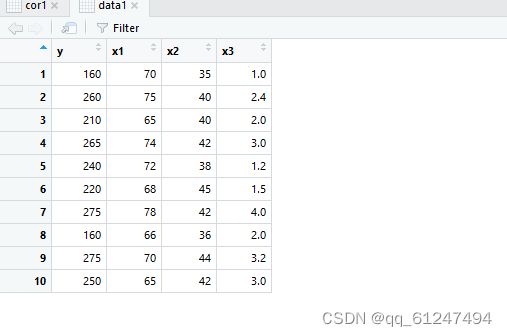
②使用data.fram()创建数据框命名为data1
如图：
- 求出y与x1，x2，x3的多元线性回归方程。
①使用lm()函数创建多元数据线性回归模型
得到coefficients（系数），x1的系数为3.754，x2的系数为7.101，x3的系数为13.447，常数项（截距）为-348.280，所以得到三元线性回归方程
y⋀=3.754x1+7.101x2+12.447x3-348.280
- 对所求的方程做拟合优度检验。
①拟合度检验：主要就是运用决定系数R²检验模型对样本观测值的拟合程度；
R²的值越接近1说明拟合程度越高
R²就是回归离差平方和SSR与总离差平方和SST的比值。（P93）
R²=SSR/SST
②使用函数summary()进行多元线性回归系数t检验
分析：残差统计量：Residuals
Min:最小值 1Q:第一四分位数 median:中位数 3Q：第三四分位数 max:最大值
系数：Coefficients
分别表示：估值（Estimate） 标准误差（Std.Error） T值（t-value） P值（Pr）
Intercept:表示截距 Month:影响因子
Multiple R-squared为模型的决定系数即R²，Adjusted R-squared为调整后的决定系数。
R²=Multiple R-squared=0.8055接近1,说明回归方程拟合度高 调整后的决定系数为0.708，说明回归方程对样本观测值的拟合程度较好。
- 对回归方程做显著性检验，对每一个回归系数做显著性检验
①对回归方程做显著性检验F检验
提出原假设H0=β1=β2=β3=0
summary(fm)
或者说P=0.01487<α=0.05，所以拒绝原假设H0,说明x与y有显著的线性关系；
②对每一个回归系数做显著性检验。（t检验）
自由度为：n-k-1=10-3-1=6
t1=1.942
t2=2.465>t0.05(6)=1.943，P2=0.0488<α=0.05，所以拒绝原假设，说明x2对y有显著的影响
t3=1.178
（5）如果有的回归系数没有通过显著性检验，将其剔除，重新建立回归方程；并做回归方程的显著性检验和回归系数的显著性检验。
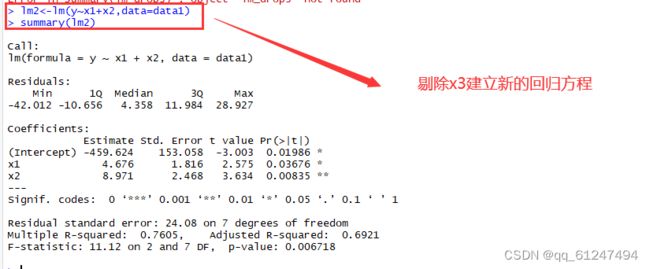
①P3=0.2835最大，剔除x3，建立新的回归方程
②重新建立回归方程y^=-459.624+4.676x1+8.971x2
③对新的回归方程做显著性检验。
提出原假设H0=β1=β2=0
summary(lm2)
P=0.006718<α=0.05，所以拒绝原假设H0,说明x与y有显著的线性关系
④对每一个回归系数做显著性检验。
自由度：10-2-1=7
summary(lm2)
t1=2.575>t0.05(7)=1.895，P1=0.03676<α=0.05，所以拒绝原假设，说明x1对y有显著的影响
t2=3.634>t0.05(7)=1.895，P2=0.00835<α=0.05，所以拒绝原假设，说明x2对y有显著的影响
- 使用逐步回归分析的逐步筛选方法获得一个最优的回归模型.
获得最优的回归模型为：y^=-34.280+3.754x1+7.101x2+12.447x3
小思考总结：
1.T检验：检验解释变量（回归系数）的显著性；
2.squared：查看方程拟合程度；
3.F检验：是检验回归方程整体显著性。