菜鸟学R语言(回归分析1)
学会用R做回归分析
在统计学中,回归分析(regression analysis)指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。回归分析按照涉及的变量的多少,分为一元回归和多元回归分析;按照因变量的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
线性回归(Linear Regression)
线性回归应该是最常用的回归了,其应用的原理就是最小二乘法。奔着少一点公式推导(不会推),多一点实例分析的原则,直接上代码。数据如下:自变量是氮含量(N),因变量是重量(weight)。下面的表格多此一举了,我只是想试试这个功能
(~ ̄▽ ̄)~
| N | 58 59 60 61 … |
|---|---|
| weight | 115 117 120 123… |
读取数据,数据结构:两个变量,15个处理
cn<-read.csv('d4.7.1.csv')
str(cn)
'data.frame': 15 obs. of 2 variables:
$ N : int 58 59 60 61 62 63 64 65 66 67 ...
$ weight: int 115 117 120 123 126 129 132 135 139 142 ...
来做个简单的线性回归看一下效果:
fit<-lm(weight ~ N, data = cn)
shapiro.test(resid(fit)) #检验正态
library(car)
ncvTest(fit) #检验方差齐性
结果如下:
> shapiro.test(resid(fit))
Shapiro-Wilk normality test
data: resid(fit)
W = 0.91909, p-value = 0.1866
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 0.8052115, Df = 1, p = 0.36954
可以看到两个p值都大于0.05,拒绝0假设,回归的没问题!
summary一下,Residuals的意思是残差~
> summary(fit)
Call:
lm(formula = weight ~ N, data = cn)
Residuals:
Min 1Q Median 3Q Max
-1.7333 -1.1333 -0.3833 0.7417 3.1167
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -87.51667 5.93694 -14.74 1.71e-09 ***
N 3.45000 0.09114 37.85 1.09e-14 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.525 on 13 degrees of freedom
Multiple R-squared: 0.991, Adjusted R-squared: 0.9903
F-statistic: 1433 on 1 and 13 DF, p-value: 1.091e-14
summary里面的信息非常全面,截距斜率,决定系数都有。
置信区间、残差,这些都是用来分析回归模型好坏的标准,具体看一下。
> confint(fit)
2.5 % 97.5 %
(Intercept) -100.342655 -74.690679
N 3.253112 3.646888
97.5%的置信区间,恩,很好,至于是怎么算的不 care
下面就是拟合值:
> fitted(fit)
1 2 3 4 5 6 7 8 9 10
112.5833 116.0333 119.4833 122.9333 126.3833 129.8333 133.2833 136.7333 140.1833 143.6333
11 12 13 14 15
147.0833 150.5333 153.9833 157.4333 160.8833
看下残差:
> residuals(fit)
1 2 3 4 5 6 7
2.41666667 0.96666667 0.51666667 0.06666667 -0.38333333 -0.83333333 -1.28333333
8 9 10 11 12 13 14
-1.73333333 -1.18333333 -1.63333333 -1.08333333 -0.53333333 0.01666667 1.56666667
15
3.11666667
残差是实际值与估计值(拟合值)之间的差。
说再多不如一幅图直观:
plot(cn$N, cn$weight,xlab="N",ylab="weight")
abline(fit)
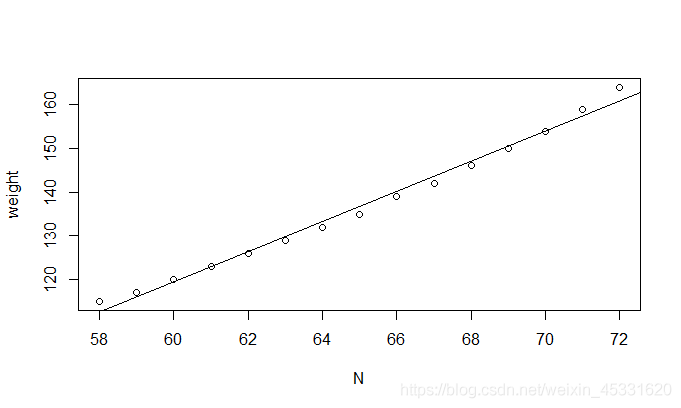
图一出来,还看个鸡毛残差置信区间啊,杠杠滴。哈哈,当然这只是个特例,前面的分析还是要有滴。
那这条拟合曲线或者说回归方程是什么呢?其实在summary里已经有了,这里再展示一下:
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -87.51667 5.93694 -14.74 1.71e-09 ***
N 3.45000 0.09114 37.85 1.09e-14 ***
ultiple R-squared: 0.991, Adjusted R-squared: 0.9903
方程就是y=3.45x-87.517,R²=0.9903。我用excel拟合了一下,R²=0.991,是没有调整之前的,事实上,调整后的R²才是准确的。但论文中标的都是R²,谁知道用的哪个,不 care
高阶线性回归
上面那个是一元一次方程,看起来效果不错,但假如我们换成一元二次方程呢?哪个更好?
cn<-read.csv( file = 'd4.7.1.csv', header = T)
fit2<-lm( weight ~ N+ I(N^2), data = cn ) # 二次项回归模型
summary(fit2) # 回归分析结果
summary的结果,可以和上一个summary对比一下。
Call:
lm(formula = weight ~ N + I(N^2), data = cn)
Residuals:
Min 1Q Median 3Q Max
-0.50941 -0.29611 -0.00941 0.28615 0.59706
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 261.87818 25.19677 10.393 2.36e-07 ***
N -7.34832 0.77769 -9.449 6.58e-07 ***
I(N^2) 0.08306 0.00598 13.891 9.32e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3841 on 12 degrees of freedom
Multiple R-squared: 0.9995, Adjusted R-squared: 0.9994
F-statistic: 1.139e+04 on 2 and 12 DF, p-value: < 2.2e-16
很明显,我们可以写出方程,y=0.083x²-7.348x+261.88
调整后R²=0.9994。这个好像拟合的更好!但不要着急下结论哦~
绘图看一下:
plot(cn$N, cn$weight,xlab="N",ylab="weight") # 绘制散点图
lines(cn$N, fitted(fit2)) # 添加回归线
> confint(fit2)
2.5 % 97.5 %
(Intercept) 206.97913605 316.77723111
N -9.04276525 -5.65387341
I(N^2) 0.07003547 0.09609252
残差:
> residuals(fit2)
1 2 3 4 5 6 7
-0.102941176 -0.473109244 -0.009405301 0.288170653 0.419618617 0.384938591 0.184130575
8 9 10 11 12 13 14
-0.182805430 0.284130575 -0.415061409 -0.280381383 -0.311829347 -0.509405301 0.126890756
15
0.597058824
对两个模型的残差做个方差分析:
> anova(fit,fit2)
Analysis of Variance Table
Model 1: weight ~ N
Model 2: weight ~ N + I(N^2)
Res.Df RSS Df Sum of Sq F Pr(>F)
1 13 30.2333
2 12 1.7701 1 28.463 192.96 9.322e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
这个我也不太懂,感觉没什么意义啊,有大神告知嘛?
真要比较哪个模型好,用AIC比较大小,很显然 fit2 更好。这个地方也有一点困惑,直接看R²不就完了,上课走神了,请大神告知。
- 假装做个记号
> AIC(fit,fit2)
df AIC
fit 3 59.08158
fit2 4 18.51270
一般来说,AIC越小越好,AIC小于4基本没差别。
回归还有好多种,比如常用的多元线性回归、逐步回归等,下一篇博客继续学习。
