最短路径专题7 最短距离-多起点多终点 (Floyd求最短路 )
题目: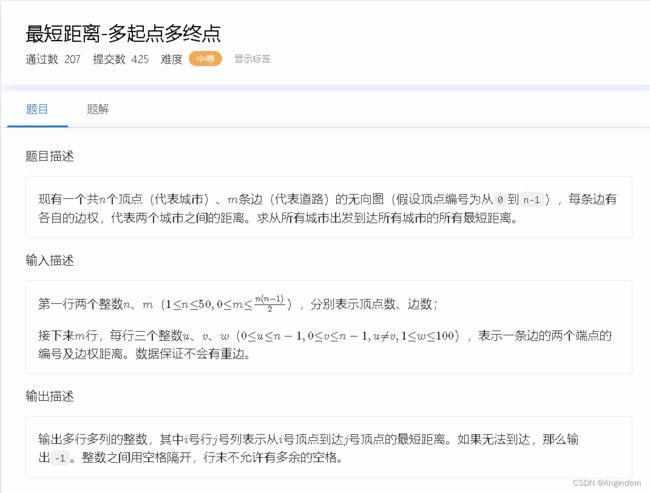
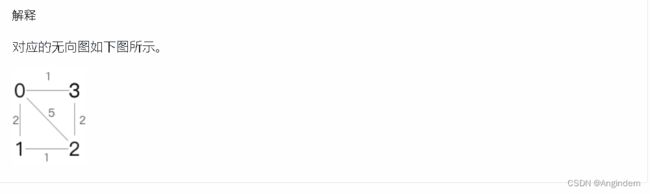
样例:
|
|
思路:
根据题目意思, 求 i 到 j 之间的最短距离或者,j 到 i 的最短距离。
这道题,因为数据范围较小,也可以直接暴力的做法,直接Dijkstra堆优化方式每次求 i 到 j 的最短距离,输出各个最短距离。
代码详解1如下:
#include
#include
#include
#include
#include
#define endl '\n'
#define mk make_pair
#define x first
#define y second
#define int long long
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define INF 0x3f3f3f3f3f3f3f
#define All(x) (x).begin(),(x).end()
#pragma GCC optimize(3,"Ofast","inline")
#define ___G std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;
// 存储 点与路径长度
using PII = pair;
int n,m,s;
int dist[N]; // 记录对应点的最短路
bool st[N]; // 标记该点是否走到过
// 数组模拟邻接表,更有效率
int h[N],e[N],w[N],ne[N],idx;
inline void Add(int a,int b,int c)
{
e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx++;
}
inline void Dijkstra()
{
// 初始化 最短路
memset(dist,INF,sizeof dist);
// 初始化起点最短路距离是 0
dist[s] = 0;
// 建立存储的 堆,根据小根堆的 小到大排序
priority_queue,greater>q;
// 这里小根堆的小到大排序规则,
// 所以我们需要距离小的排前面,点放在后面
q.push(mk(0,s));
// 这里有一点点类似 BFS 做法
while(q.size())
{
// 取出我们对应最短距离需要更新的堆组合
auto now = q.top();
q.pop();
int a = now.y; // 取出对应的点
int distence = now.x; // 取出对应的最短距离
if(st[a]) continue; // 如果我们点走动过,就不用更新走动了
st[a] = true; // 标记当前走动更新的点
// 更新该点的 dist
for(int i = h[a];i != -1;i = ne[i])
{
int j = e[i]; // 取出对应点的关系
// 如果该点j的距离 比 a 点到 j 点的距离还要大,那么更新最短路径距离
if(dist[j] > distence + w[i]) dist[j] = distence + w[i];
// 存储对应距离和对应点,方便下一次更新
q.push(mk(dist[j],j));
}
}
return ;
}
inline void solve()
{
// 链表初始化
memset(h,-1,sizeof h);
cin >> n >> m;
while(m--)
{
int a,b,c;
cin >> a >> b >> c;
// 添加链表,记录两点之间的距离
Add(a,b,c);
Add(b,a,c);
}
for(int i = 0;i < n;++i)
{
s = i;
memset(st,false,sizeof st);
Dijkstra();
// 输出各点的所得最短距离
for(int j = 0;j < n;++j)
{
if(j)cout << ' ';
if(dist[j] >= INF) cout << 0;
else cout << dist[j];
}
cout << endl;
}
}
signed main()
{
// freopen("a.txt", "r", stdin);
___G;
int _t = 1;
// cin >> _t;
while (_t--)
{
solve();
}
return 0;
} 最后提交:
第二种解法:
Floyd算法,直接定义 两个点之间的最短距离,注意初始化两个点之间的最短距离
核心就是三层循环的暴力做法,每一层循环的含义就是:起点,中间连接点,终点。
代码详解2如下:
#include
#include
#include
#include
#include
#include
#define endl '\n'
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define INF 0x3f3f3f3f3f3f
#define All(x) x.begin(),x.end()
#pragma GCC optimize(3,"Ofast","inline")
#define ___G std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10,M = 500;
int n,k;
int dist[M][M]; // 记录各个点之间的最短距离
// 初始化操作
inline void Floyd()
{
// 这一层做中间点
for(int it = 0;it < n;++it)
{
// 这一层做 i 点
for(int i = 0;i < n;++i)
{
// 这一层做 j 点
for(int j = 0;j < n;++j)
{
// 选择最短距离方案,
// i 到 it ,it 到 j 的距离和 直接 i 到 j 的距离哪个是最短距离
// 就选择哪个
dist[i][j] = min(dist[i][j],dist[i][it] + dist[it][j]);
}
}
}
}
inline void Init()
{
// 初始化所有点之间的边长为无穷
memset(dist,INF,sizeof dist);
// 自身点之间距离是 0
for(int i = 0;i <= n;++i)
{
dist[i][i] = 0;
}
}
inline void solve()
{
cin >> n >> k;
// 初始化操作
Init();
while(k--)
{
int a,b,c;
cin >> a >> b >> c;
// 记录两点之间的最短距离
dist[a][b] = dist[b][a] = min(dist[a][b],c);
}
Floyd();
// 输出各个点之间的最短距离
for(int i = 0;i < n;++i)
{
for(int j = 0;j < n;++j)
{
if(j) cout << ' ';
cout << dist[i][j];
}
cout << endl;
}
}
int main()
{
// freopen("a.txt", "r", stdin);
___G;
int _t = 1;
// cin >> _t;
while (_t--)
{
solve();
}
return 0;
} 最后提交:
从提交的结果可以知道,当有多起点多终点的时候,最好用 Floyd 算法,时间复杂度低,代码简易有效率,如果暴力 Dijkstra ,时间复杂度相比较高,代码较多效率低。
Floyd算法,灵活性差,Dijkstra灵活性高。