深入理解 原码,反码,补码——证明补码等于反码加1
文章目录
- 前言
- 利用同余数 直接得到 补码
-
- 同余数
- 推导
- 总结
- 从原码到反码到补码
-
- 原码
- 反码
-
- 反码的问题
- 解决反码出错的式子
- 总结
- 补码
-
- 补码解决了跨越问题
- 为什么补码等于反码+1
前言
根据冯~诺依曼提出的经典计算机体系结构框架,计算机里只有加法器而没有减法器,所以在加法器的眼里,不管是正数还是负数,都会按照无符号数的加法来加(这里的加法,就是指我们正常的加法,按位进1的那个)。
所以我们需要研究一种码,能把负数的符号位也参与进运算来。使得加法器,在遇到:
- a + b时,执行加法
- a - b时,转换为a + (-b),再执行加法。注意此时,加法器是不关心这个(-b)是一个负数的,它会按照同样的加法规则进行计算。
利用同余数 直接得到 补码
以4位bit的数值为例,我们开始分析。

如果只以4位bit的数值的正数部分来看,我们只执行加法的话,现有加法器完全可以应付。
我们现在需要设计出一种码,可以应付减法,已知条件是:最高位bit将作为符号位,即这个bit是有具体特殊功能的。所以上表到了0111就结束了。
同余数
如果 a%m = b%m,那么说明a和b是m的同余数。顾名思义,即a和b相对于m的余数是相同的。
那么已知 a和m,怎么得到a的另一个相邻的同余数呢,可以令b = a + m。
推导
已知 3 + 5 = 7,现在让等式变成 3 + 5对于16的同余数 应该也等于 7。因为4位bit的范围是0-15(因为加法器只把数看做无符号数,所以这里到15),两个数无论怎么加,肯定是在对16取余。
- 3 + 5 = 7
- 5对于16的同余数为 21,21的二进制为
10101,被截断后为0101,所以还是为5。 - 所以3 + 5 = 3 + 21 = 3 + 5 = 8。
- 第一个=是替换为同余数,第二个=是同余数21被截断。
现在回到问题“我们现在需要设计出一种码”:
- 已知要求得3 - 1,但现在没有减法器
- 利用同余数,变换为 3 - 1 = 3 + (-1) = 3 + (-1 + 16) = 3 + 15
- 15对应的二进制为
1111,3的二进制直接看上表是0011 - 那么就是
0011+1111=10010,被截断后为0010。 - 验证成功,
0010确实是2的二进制。
已经证明了被减数可以用同余数替换,现在试试 如果减法的结果是负数的话,得到的负数 是否也符合同余数变换:
- 已知要求得3 - 5
- 利用同余数,变换为 3 - 5 = 3 + (-5) = 3 + (-5 + 16) = 3 + 11
- 11对应的二进制为
1011,3的二进制直接看上表是0011 - 那么就是
0011+1011=1110。 - 那么
1110就应该是-2的二进制。- 利用同余数,-2的同余数可以是14,14的二进制就是
1110。验证成功。
- 利用同余数,-2的同余数可以是14,14的二进制就是
通过上面两条证明,得知 负数可以用它的同余数的二进制来替换,这个同余数特指0-15范围内的同余数(因为是4bit的数值)。
总结
负数的补码的二进制 = 负数的同余数 = 负数 + 模(+模其实指的是加整数个模,目的是为了让 负数 + 模 肯定得到 一个0~15的正数)- 因为
负数的补码的二进制 = 负数 + 模,所以负数的补码的二进制 = 模 - |负数|(|负数|取负数的绝对值)
从原码到反码到补码
原码
原码:是最简单的机器数表示法。用最高位表示符号位,‘1’表示负号,‘0’表示正号。其他位存放该数的二进制的绝对值。

如上,两个相反数之间,只是符号位不一样,但是负数出现了-0这种东西。
0000 + 1000 = 1000,即 0 + (-0) = -0,考虑到正零和负零是一样的,这个式子是对的。
0001 + 1001 = 1010,即1 + (-1) = -2,这个式子就不能成立了。
反码
正数的反码还是等于原码
负数的反码就是他的原码除符号位外,按位取反。
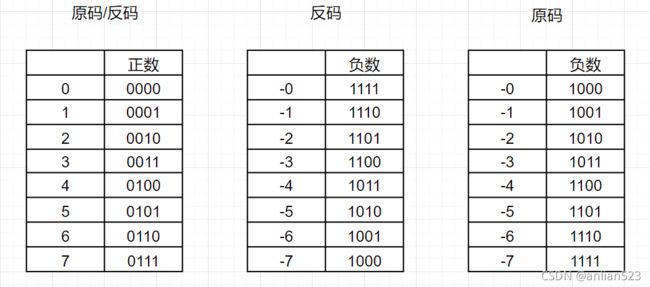
从上图可以看出,负数从小到大(从-7到-0),它们的二进制也是递增的(从1000到1111)。从这一点上来看,反码更加合理。
反码的问题
0001 + 1110 = 1111,即1 + (-1) = -0,现在反码最起码解决了互为相反数相加的问题。
1110(-1)+1101(-2)= 11011 = 截断后为1011(-4),现在这个式子却出了问题。
1110(-1)+0010(2)= 10000 = 截断后为0000(0),同样有问题。
解决反码出错的式子
那么如何解决 反码相加最后结果却出问题的式子呢,这里直接给出答案:
让出问题的式子的结果再加1。接下来给出解释:
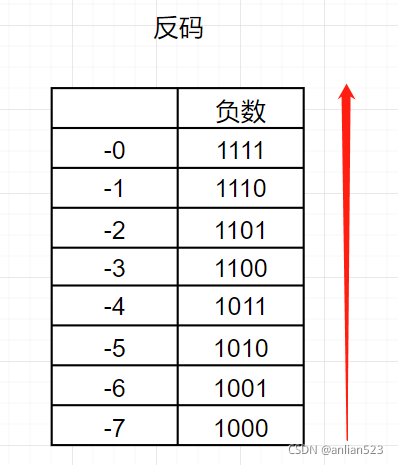
我们知道一个二进制0000不停地加0001的话,由于会被截断,这个二进制会不停循环0000~1111,如下图:

现在观察这个错误式子:1110(-1)+0010(2)= 10000 = 截断后为0000(0)

发现上图过程,跨越了1111这个坎(从而到达了0000),但依次到达的两个数却分别是1111(-0)、0000(0),但我们想要的效果为:依次到达0(不管这个0是正零还是负零)、1。那么很简单,每当发现跨越了1111这个坎,我们就让结果加1,因为从1111(-0)到达0000(0)白跑了一趟。所以这个错误式子让结果加1就好了。
再观察这个错误式子:1110(-1)+1101(-2)= 11011 = 截断后为1011(-4)

同样的,也跨越了1111这个坎,但是呢,只跨越了一次,所以这个错误式子只需要加1即可。
可能同学们想问,要是跨越了两次1111怎么办:

那么很简单,让结果加2就好了,因为跨越了两次。2就是上面的红色的10。但是实际上,就算是两个最大的反码数1111相加,结果为11110,也只会发生一次跨越。除非两个以上的反码数相加,才可能跨越多次。
但是写程序总不能去判断有没有发生跨越吧(好像得写个if),但我们有一个巧妙的方法(避开使用if):
- 已知
char的bit长度为8bit,我们再假设一个新的数据类型为halfchar,其bit长度为4bit。 - 那么执行如下代码即可:
char sum = 0; halfchar a; halfchar b;//假设a和b都已经有值了
sum += a;
sum += b;//此时sum的高4bit可能变成了0001,因为产生了一次跨越
sum = (sum>>4) + (sum&0xf);
- 如果sum高4bit为全0,那么执行
(sum>>4) + (sum&0xf)不会改变sum。 - 如果sum高4bit不为全0,那么执行
(sum>>4) + (sum&0xf)会让sum再加1。这和之前讲的“发生一次跨越,就让结果加1”一样。
总结
- 两个反码数相加,如果跨越了
1111这个坎,且不考虑截断的话,和的高4bit必为0001,因为只会有一次跨越。 - 两个反码数相加,只会跨越了一次
1111这个坎,结果需要加1。多于两个的反码数相加,则才可能跨越不止一次1111这个坎。 - 跨越两次需要加2。以此类推。
- 实际代码为:
sum = (sum>>4) + (sum&0xf)。
补码
正数的补码等于它的原码
负数的补码等于反码+1。(这只是一种算补码的方式)
负数的补码等于他的原码自低位向高位,尾数的第一个‘1’及其右边的‘0’保持不变,左边的各位按位取反,符号位不变。

从“负数的补码等于反码+1”来看,-1到-7在加1后,没有发生溢出,所以对应关系没有发生变化。而1111再加1后就会溢出,溢出后变成10000,截断后为0000是在正数范围不能用;而1000却多余了出来,这里让它代表-8。

单独看补码,数值与其对应的二进制也是递增的。
补码解决了跨越问题
之前的反码在跨越1111这个坎时,会遇到两个0(负零和正零)。现在观察补码,发现从1110到1111再到0000,它们的数值是依次递增的,这就解决了在反码中遇到的 跨越1111 的问题。
为什么补码等于反码+1
- 首先有
负数的反码 + |负数| = 1111(反码就是除符号位外各个位取反,然后这两个的符号位也是相反的,所以相加为全1;|负数|不用强调是什么码,因为它是一个正数,正数的各个码相同) 0001 + 负数的反码 + |负数| = 1111 + 0001(两边各加1),即0001 + 负数的反码 + |负数| = 10000,因为10000就是4bit数值的模,所以0001 + 负数的反码 + |负数| = 模- 之前的利用同余数直接得到补码章节已经推导得到
负数的补码的 = 模 - |负数|,那么|负数| = 模 - 负数的补码 - 将
|负数| = 模 - 负数的补码代入到0001 + 负数的反码 + |负数| = 模,得到0001 + 负数的反码 + 模 - 负数的补码 = 模,同时去掉模,那么得到0001 + 负数的反码 = 负数的补码,证毕。