2018南京ICPC现场赛部分题题解

Problem A. Adrien and Austin

题意：

给你n个石子，下标从1到n，每次最多取连续的k个石子，问最后谁能赢（取完石子的那个人算赢）。

思路：

如果有奇数个石子，那么A中间取一个，B拿什么，A接下去就在对称的另一边拿什么，这样A赢。

如果有偶数个石子，且b>1 ,那么A可以在中间取两个，然后又回到了上述的过程，这样A赢。如果b==1，那么石子是偶数个，则B赢。

注意特殊情况：一开始有0个石子，那么就是B赢。

AC Code

#include
using namespace std;
int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    if(n==0) printf("Austin\n");
    else if(n%2==1) printf("Adrien\n");
    else
    {
        if(k==1) printf("Austin\n");
        else printf("Adrien\n");
    }
    //system("pause");
    return 0;
}

Problem D. Country Meow

题意：

最小球覆盖。在三维坐标系中给你n个点的坐标，求出到所有点的最大距离的最小值。

思路：

三分法的嵌套。三分x坐标（三分y坐标（三分z坐标））。

AC Code

#include
using namespace std;
int n;
struct Node
{
    double x,y,z;
}node[105];
double dis(double x1,double y1,double z1,double x2,double y2,double z2)
{
    return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)+(z1-z2)*(z1-z2));
}
double cal(double x,double y,double z)//x,y,z都确定
{
    double res=0;
    for(int i=1;i<=n;i++)
        res=max(res,dis(x,y,z,node[i].x,node[i].y,node[i].z));
    return res;
}
double cal(double x,double y)//x和y已经确定
{
    double l=-100000,r=100000,ans=1e18;
    for(int i=1;i<=50;i++)
    {
        double mid=(l+r)/2;
        double m=(mid+r)/2;
        double ans1=cal(x,y,mid);
        double ans2=cal(x,y,m);
        if(ans1>ans2) l=mid;
        else r=m;
        ans=min(ans,ans1);
        ans=min(ans,ans2);
    }
    return ans;
}
double cal(double x)//x已经确定
{
    double l=-100000,r=100000,ans=1e18;
    for(int i=1;i<=50;i++)
    {
        double mid=(l+r)/2;
        double m=(mid+r)/2;
        double ans1=cal(x,mid);
        double ans2=cal(x,m);
        if(ans1>ans2) l=mid;
        else r=m;
        ans=min(ans,ans1);
        ans=min(ans,ans2);
    }
    return ans;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%lf%lf%lf",&node[i].x,&node[i].y,&node[i].z);
    double l=-100000,r=100000,ans=1e18;
    for(int i=1;i<=50;i++)
    {
        double mid=(l+r)/2;
        double m=(mid+r)/2;
        double ans1=cal(mid);
        double ans2=cal(m);
        if(ans1>ans2) l=mid;
        else r=m;
        ans=min(ans,ans1);
        ans=min(ans,ans2);
    }
    printf("%.7f\n",ans);
    //system("pause");
    return 0;
}

Problem G. Pyramid

题意：

找有多少个等腰三角形

思路：

打表可得规律: n(n+1)(n+2)(n+3) / 24;(除法时要用逆元)

AC Code

#include
using namespace std;
typedef long long LL;
LL mod=1e9+7;
LL quick_pow(LL x,LL y)
{
    LL res=1;
    while(y)
    {
        if(y%2) res=res*x%mod;
        x=x*x%mod;
        y=y/2;
    }
    return res%mod;
}
int main()
{
    int t;
    scanf("%d",&t);
    LL ans=quick_pow(24,mod-2);
    while(t--)
    {
        LL n;
        scanf("%lld",&n);
        LL res=1;
        res=res*n%mod;
        res=res*(n+1)%mod;
        res=res*(n+2)%mod;
        res=res*(n+3)%mod;
        res=res*ans%mod;
        printf("%lld\n",res);
    }
    //system("pause");
    return 0;
}

Problem I.Magic Potion

题意：

给定n个英雄，m只怪兽，k瓶强化药剂。每个英雄只能杀一只怪，一个英雄磕了药之后能够多杀一只，但是一个英雄至多只能磕一次药。已知每个英雄能够杀死哪些怪兽，问最多杀死几只怪。

思路：

网络最大流的关键在于建图。添加源点和两个中间结点，编号分别为1,2，3。再添加n个结点表示英雄，编号为4——n+3。再添加m个结点表示怪兽，编号为n+4——n+m+3。最后添加汇点，编号为n+m+4。

连接源点和两个中间结点，容量分别为n和k。将每个英雄和两个中间结点相连，容量为1。将每个英雄和他能消灭的怪兽相连，容量为1。最后将每个怪兽和汇点连接，容量为1。

跑Dinic算法即可。

AC Code

#include
using namespace std;
const int N=2000,inf=1<<30;
int head[N],cent=0;
int s,t;//超级源点和超级终点
int maxflow=0;
int dep[N],ans[N],vir[N];//在bfs分层时所用
struct Node
{
    int v,val;
    int next;
}node[N*10];
void add(int u,int v,int val)
{
    node[cent].v=v;
    node[cent].val=val;
    node[cent].next=head[u];
    head[u]=cent++;
}
bool bfs()
{//分层
    for(int i=0;i<=t+10;i++)
    {
        dep[i]=0x3f3f3f3f;
        ans[i]=0;
        vir[i]=head[i];
    }
    queue<int>q;
    q.push(s);//将超级源点加入队列中，并初始化。
    dep[s]=0;
    while(!q.empty())
    {
        int now=q.front();
        q.pop();
        ans[now]=0;
        for(int i=head[now];~i;i=node[i].next)
        {
            int to=node[i].v;
            if(dep[to]>dep[now]+1&&node[i].val)
            {
                dep[to]=dep[now]+1;
                if(ans[to]==0)
                {
                    ans[to]=1;
                    q.push(to);
                }
            }
        }
    }
    if(dep[t]!=0x3f3f3f3f) return 1;
    return 0; 
}
int dfs(int u,int flow)
{
    int rlow=0;
    if(u==t)
    {
        maxflow+=flow;
        return flow;
    }
    int used=0;
    for(int i=vir[u];~i;i=node[i].next)
    {
        vir[u]=i;
        int d=node[i].v;
        if(node[i].val&&dep[d]==dep[u]+1)
        {
            if(rlow=dfs(d,min(flow-used,node[i].val)))
            {
                used+=rlow;
                node[i].val-=rlow;
                node[i^1].val+=rlow;
                if(used==flow) break;
            }
        }
    }
    return used;
}
int Dinic()
{
    while(bfs())
    {
        dfs(s,inf);
    }
    return maxflow;
}
int main()
{
    memset(head,-1,sizeof(head));
    int n,m,k;
    scanf("%d%d%d",&n,&m,&k);
    add(1,2,n),add(2,1,0);//1号点为源点，2号点和3号点为中间点
    add(1,3,k),add(3,1,0);
    s=1,t=4+n+m;//源点和汇点
    int a1=4,a2=3+n,a3=3+n+m;//编号4——3+n为超人,编号4+n——3+n+m为怪兽
    for(int i=4;i<=3+n;i++)
    {//建图
        add(2,i,1),add(i,2,0);//每个英雄与中间点相连
        add(3,i,1),add(i,3,0);
        int num;
        scanf("%d",&num);
        while(num--)
        {
            int x;
            scanf("%d",&x);
            add(i,a2+x,1);//每个英雄与自己能打败的怪兽相连
            add(a2+x,i,0);
        }
    }
    for(int i=a2+1;i<=a3;i++)//每个怪兽与汇点相连
        add(i,t,1),add(t,i,0);
    printf("%d\n",Dinic());//跑Dinic
    //system("pause");
    return 0;
}

Problem J. Prime Game

题意：

给你一个长度为n的序列ai，fac(l,r)为第l个数到第r个数的不同素因子的数量和，现在求解

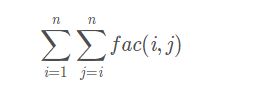
思路：

这样的计数题，要考虑每个质因子的贡献。我们可以计算所有质因子出现的位置压入vector中。计算每一个位置上的质因子对于答案的贡献。

AC Code

#include
using namespace std;
typedef long long LL;
const int N=1e6+10;
vector<int>a[N];
int primes[N],ans[N],idx=0;
void resolve(int pos,int x)
{//素因子分解
    int k=1;
    while(primes[k]*primes[k]<=x)
    {
        if(x%primes[k]==0)
        {
            a[primes[k]].push_back(pos);
            while(x%primes[k]==0)
                x/=primes[k];
        }
        k++;
    }
    if(x>1) a[x].push_back(pos);
}
int main()
{
    for(int i=2;i<=N;i++)
    {//欧拉筛筛素数
        if(ans[i]==0) primes[++idx]=i;
        for(int j=1;j<=idx&&primes[j]*i<N;j++)
        {
            ans[primes[j]*i]=1;
            if(i%primes[j]==0) break;
        }
    }
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        int x;
        scanf("%d",&x);
        resolve(i,x);
    }
    LL res=0;
    for(int i=0;i<=N;i++)
    {
        if(!a[i].size()) continue;
        for(int j=0;j<a[i].size();j++)
        {   //计算每个素因子在不同位置上的贡献
            if(j==0) res+=(LL)a[i][j]*(n-a[i][j]+1);
            else res+=(LL)(a[i][j]-a[i][j-1])*(n-a[i][j]+1);
        }
    }
    printf("%lld\n",res);
    //system("pause");
    return 0;
}

Problem K. Kangaroo Puzzle

题意：

有一个n*m地图，每个方块标记为0和1, 1的方块表示可以通行并且在最开始的时候有一只袋鼠，0的方块表示不能通行。可以对所有袋鼠进行上下左右四个方向的操作。问如何在50000次操作内把所有袋鼠聚集在一个方块。

思路：

随机化（看了别的博主的代码，但我还不能证明，为什么对。。。）

AC Code

#include
using namespace std;
char s[25][25];
int n,m;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%s",s[i]);
    srand(time(0));
    char str[4]={'L','R','U','D'};
    for(int i=1;i<=20;i++) printf("U");
    for(int i=1;i<=20;i++) printf("R");
    for(int i=1;i<=20;i++) printf("D");
    for(int i=1;i<=20;i++) printf("L");
    for(int i=1;i<=49920;i++)
    {
        int x=rand()%4;
        printf("%c",str[x]);
    } 
    return 0;
}