人工智能——智能控制【2】优化算法

（若有侵权请立刻联系笔者删除）
智能控制的上一篇博文介绍了神经网络的初步认知，尤其是对于最后动物的分类特别有意思，大家可以看一下上一次的网络模型亲自实践一下感受神经网络的有趣，这次主要是说一下智能控制的遗传算法和粒子群算法：

1.粒子群优化算法

（1）理论讲解
粒子群算法是什么呢？这个是仿生蚂蚁所得到的的一种算法，简而言之，一群蚂蚁在点对点搬运物体的时候，一开始会走不同的路线最后到达目的地，最短的路线上气味分布的相对更浓，蚂蚁会判断气味更浓的地方从而走这条路线，越多的蚂蚁走最近的路线从而气味越弄，从而使更多的蚂蚁走最短的路线，最后得到这条最短的路线，这就是粒子群算法的优化模型。
粒子群算法的数学模型如下：

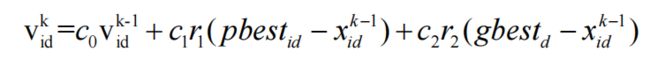
右侧由三部分组成：自身速度、自我认知部分和社会经验部分，带best的都是最好的位置分别是个体经历过的最好位置和种群经历的最好位置，c都是修正系数，其他则为位置和速度矢量。整个过程就是初始化粒子群体随机位置和速度->评价粒子的适应度->找到历史最佳位置->找到群体最佳位置->更新位置和速度。可能有人会问，这个公式没有出现更新后的位置矢量：

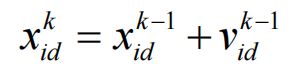
在这个大型的群体中，如果将所有个体都作为粒子的邻域，那么就是全局粒子群算法，收敛速度快，但可能局部最优；如果只是部分个体作为邻域，那么就是局部粒子群算法，很难陷入局部最优。
（2）最大值求解应用
那下面实战一下吧！求下面函数最大值：我们先绘制下面函数的形状：

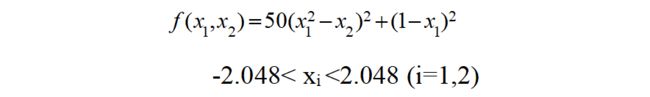
fun=@(x1,x2) (50*(x1.^2-x2).^2+(1-x1).^2);
fsurf(fun,[-2.048 2.048 -2.048 2.048],'ShowContours','on');
xlabel('x1');ylabel('x2');zlabel('函数值：f');title('原函数');
box on

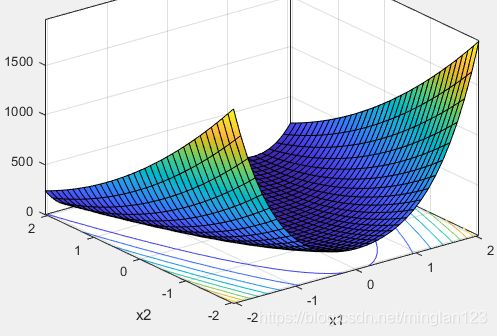
得到的结果是不是这样的呢？我们可以看到最大值的大体存在于两个峰点。下面话不多说，直接上matlab代码：

clc;clear;close all;
%% 初始化参数
min=-2.048;max=2.048;%粒子位置范围
Vmax=1;Vmin=-1;      %粒子运动速度范围
c1=1.3;c2=1.7;       %学习因子
wmin=0.10;wmax=0.90; %最佳线性惯性权重范围
G=100;               %最大迭代次数
Size=50;              %初始化群体个体数目
M=1;                 %1为局部最优，2为全局最优
%% 线性化惯性权重
for i=1:G
    w(i)=wmax-((wmax-wmin)/G)*i;  %随着优化进行，不断降低自身权重
end  
%% 随机初始粒子位置和速度
for i=1:Size
    for j=1:2
        x(i,j)=min+(max-min)*rand(1);     %随机初始化位置
        v(i,j)=Vmin +(Vmax-Vmin)*rand(1); %随机初始化速度
    end
end
%% 计算各个粒子的适应度，并初始Pi、plocal(局部最优值)和最优个体BestS（全局最优）
for i=1:Size
    p(i)=chap10_3func(x(i,:));
    y(i,:)=x(i,:);
    if i==1
        plocal(i,:)=chap10_3lbest(x(Size,:),x(i,:),x(i+1,:));
    elseif i==Size
        plocal(i,:)=chap10_3lbest(x(i-1,:),x(i,:),x(1,:));
        else 
        plocal(i,:)=chap10_3lbest(x(i-1,:),x(i,:),x(i+1,:));
    end
end
BestS=x(1,:);  %初始化最优个体BestS
for i=2:Size
    if chap10_3func(x(i,:))>chap10_3func(BestS)
        BestS=x(i,:);
    end
end
%% 迭代过程
for kg=1:G
    for i=1:Size
      if M==1
         v(i,:)=w(kg)*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(plocal(i,:)-x(i,:));%局部寻优：加权，实现速度的更新
      elseif M==2
         v(i,:)=w(kg)*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(BestS-x(i,:));      %全局寻优：加权，实现速度的更新
      end
          for j=1:2                                                               %检查速度是否越界
            if v(i,j)<Vmin
                v(i,j)=Vmin;
            elseif  x(i,j)>Vmax
                v(i,j)=Vmax;
            end
          end
        x(i,:)=x(i,:)+v(i,:);                                                     %实现位置的更新
        for j=1:2                                                                 %检查位置是否越界
            if x(i,j)<min
                x(i,j)=min;
            elseif  x(i,j)>max
                x(i,j)=max;
            end
        end         
%自适应变异,避免粒子群算法陷入局部最优
       if rand>0.60
            k=ceil(2*rand);
            x(i,k)=min+(max-min)*rand(1);
       end
%判断局部最优值
       if i==1
            plocal(i,:)=chap10_3lbest(x(Size,:),x(i,:),x(i+1,:));
        elseif i==Size
            plocal(i,:)=chap10_3lbest(x(i-1,:),x(i,:),x(1,:));
        else 
            plocal(i,:)=chap10_3lbest(x(i-1,:),x(i,:),x(i+1,:));
        end
%判断最大值
       if chap10_3func(x(i,:))>p(i) %判断当此时的位置是否为最优的情况，当不满足时继续更新
          p(i)=chap10_3func(x(i,:));
          y(i,:)=x(i,:);
       end
%判断全局最大值
        if p(i)>chap10_3func(BestS)
            BestS=y(i,:);
        end
    end
Best_value(kg)=chap10_3func(BestS);
end
figure(1);
kg=1:G;
plot(kg,Best_value,'r','linewidth',2);
xlabel('generations');ylabel('Fitness function');

关于其中的部分chap10_3func（）函数和chap10_3lbest（）函数就是一个函数的表达值和求最优值的函数：

//函数值表达式
function f = func(x)
f=50*(x(1)^2-x(2))^2+(1-x(1))^2;
//最优值求解
function f =evaluate_localbest(x1,x2,x3)%求解粒子环形邻域中的局部最优个体
K0=[x1;x2;x3];
K1=[chap10_3func(x1),chap10_3func(x2),chap10_3func(x3)];
[maxvalue index]=max(K1);
plocalbest=K0(index,:);
f=plocalbest;

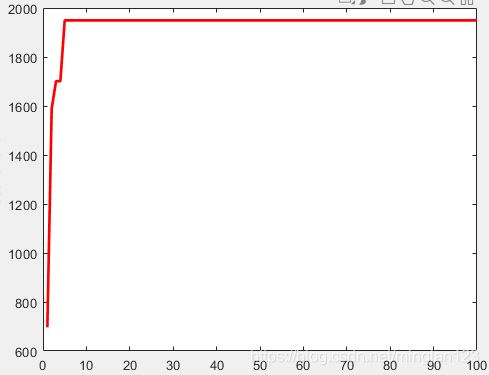
各位可以运行试试看，修改不同的种群数量，最后得到最大值点为【-2.048 -2.048】，最大值为1957.6。同时给出粒子群数目为10的最大值迭代变化：

2.遗传算法

遗传算法则是模拟遗传类的知识，遗传和变异决定了生物的发展方向，适者生存优胜劣汰，主要一个问题便是对环境的适应度，对适应度进行判断从而实现优中选优的一个思想，这也算是达尔文进化论的一种验证：

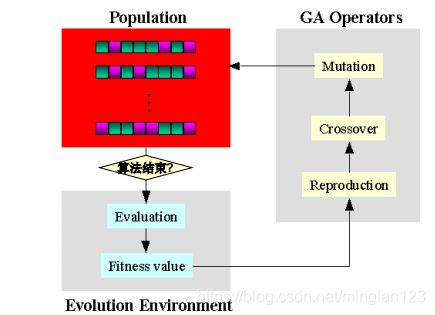
我们知道了一个大体思想，那么接下来便要看如何实现这种思想，最重要的是对种群进行适应度的分析和进一步优化，生物的表观印象不能被计算机读取，因此需要编码和解码，这一块也是很基础的不再说了。对于计算机方面的GA算法，大体可以描述为：输入-编码-判断是否满足终止条件-计算适应度-不满足则执行遗传算子，并分别进行复制、交叉和变异-满足则输出结果。复制和交叉以及变异的过程也十分符合达尔文的生物进化论，因此整个迭代过程是十分有意思的。
依旧对上述函数进行拟合，这次我们将每次迭代中设置好遗传、变异和交叉，对应交叉可能影响不是很大，遗传保留并扩大了最大值的涵盖面，而对于变异则增加了不确定性。不多说，直接上代码：

clear;clc;close all;
%% 初始参数
Size=80;                         %群体大小
gene=100;                        %终止进化代数  
CodeL=10;                        %编码位数
umax=2.048;umin=-2.048;          %限定范围
E=round(rand(Size,2*CodeL));     %初始群体样本
%% 主迭代过程
for k=1:1:gene
  for s=1:1:Size
  m=E(s,:);                      
  y1=0;y2=0;              
  m1=m(1:1:CodeL);                %获得样本前半部分
    for i=1:1:CodeL
       y1=y1+m1(i)*2^(i-1);       %解码
    end
  x1=(umax-umin)*y1/1023+umin;   
  m2=m(CodeL+1:1:2*CodeL);        %获得样本后半部分
    for i=1:1:CodeL
       y2=y2+m2(i)*2^(i-1);       %解码
    end
  x2=(umax-umin)*y2/1023+umin;    
  F(s)=50*(x1^2-x2)^2+(1-x1)^2;  
  end                     
%% ******步骤一：判断是否为最优值******
fi=F;                             %适应度函数
[Oderfi,Indexfi]=sort(fi);        %从小到大排序
Bestfi=Oderfi(Size);              %获得当前最大值
BestS=E(Indexfi(Size),:);    
bfi(k)=Bestfi;   
%% ******步骤二：选择并复制******
   fi_sum=sum(fi);                %所有值求和
   fi_Size=(Oderfi/fi_sum)*Size;  
   fi_S=floor(fi_Size);      
   kk=1;
   for i=1:1:Size
      for j=1:1:fi_S(i)           %复制
       TempE(kk,:)=E(Indexfi(i),:);
       kk=kk+1;
      end
   end 
%% ************步骤三：交叉************
pc=0.60;                          %交叉概率
n=ceil(20*rand);             
for i=1:2:(Size-1)
    temp=rand;
    if pc>temp             
    for j=n:1:20
        TempE(i,j)=E(i+1,j);
        TempE(i+1,j)=E(i,j);    
    end
    end
end
TempE(Size,:)=BestS;            
%% ************步骤四：变异**************
pm=0.1;                           %变异概率
   for i=1:1:Size
      for j=1:1:2*CodeL
         temp=rand;
         if pm>temp               
            if TempE(i,j)==0
               TempE(i,j)=1;
            else
               TempE(i,j)=0;
            end
        end
      end
   end
TempE(Size,:)=BestS;
E=TempE;                        
end
%% 输出最后结果
disp(['最大值：',num2str(Bestfi),'坐标：',num2str(x1),' ',num2str(x2)]);
time=1:gene;figure(1);
plot(time,bfi,'linewidth',2);
xlabel('generation');ylabel('maxvlue');

最后的结果与PSO算法是一样的，也就证明我们的结果正确！

3.算法比较

（1）遗传算法收敛速度较慢，粒子群算法收敛速度较快；
（2）粒子群算法更容易陷入局部最优解，而且算法不稳定，局部寻优的PSO有了明显的改善；遗传算法可以通过交叉变异跳出局部最优；

这两种算法在寻找最优值中都有着广泛的应用，对于算法的创新也十分有基础，如果可以的话建议读者自行深入学习理论并亲自撰写代码，或者读懂本篇文章代码后，在不看的情况下自行再编撰出来，相信对于算法研发会有很好的进步。最后，还是那句话，有想交流讨论一起进步的欢迎私聊或者评论，大家一起加油！