智能优化算法：原子搜索优化算法 -附代码

智能优化算法：原子搜索优化算法

摘要：原子搜索优化算法（Atom Search Optimization）是于2019提出的一种基于分子动力学模型的新颖智能算法．模拟在原子构成的分子系统中，原子因相互间的作用力和系统约束力而产生位移的现象．在一个分子系统中，相邻的原子间存在相互作用力（吸引力和排斥力），且全局最优原子对其他原子存在几何约束作用 ．引力促使原子广泛地探索整个搜索空间，斥力使它们能够有效地开发潜在区域 。具有寻优能力强，收敛快的特点。

1.原子优化算法原理

假设一个分子系统是由 s个原子构成的d维空间, $X_i^d(t)$）为第$i$ 个原子在第$t$次迭代时的位置，可以表示为:$X_i^d(t)=(X_{i,1},X_{i,2},...,X_{i,d}),(i=1,2,...,s;,t=1,2,...,t_{max}$,$t_{max}$为最大迭代次数,$X_{best}^d(t)$）为第t次迭代时全局最优解．

图1.n，F 和h关系图

原子运动遵循经典力学根据牛顿第二定律，原子的加速度与其质量有关，且由原子间的相互作用力和最优原子对其的几何约束的共同作用产生，所以第i个原子在第t次迭代时加速度如下：
$$a_i^d(t)=\frac{F_i^d+G_i^d(t)}{m_i^d(t)}\text{\hspace{1em}(1)}$$
式中，$F_i^d(t)$为第t次迭代时d维空间中作用于第 i个原子的总力，可以看作是适应度函数值较好的k个原子对第i个原子作用力的随机加权之和，表示如下:
$$F_i^d(t)=\sum _{j\in K_{best}}ran{d}_j{F}_{ij}^d(t)\text{\hspace{1em}(2)}$$
式中，$K_{best}$为适应度函数值较好的$k$个原子的集合，$F_{ij}^d$为两原子之间的作用势能，可以表示为：
$$F_{ij}^d=-n(t)[2(h_{ij}(t){)}^3-(h_{ij}(t){)}^7]\text{\hspace{1em}(3)}$$
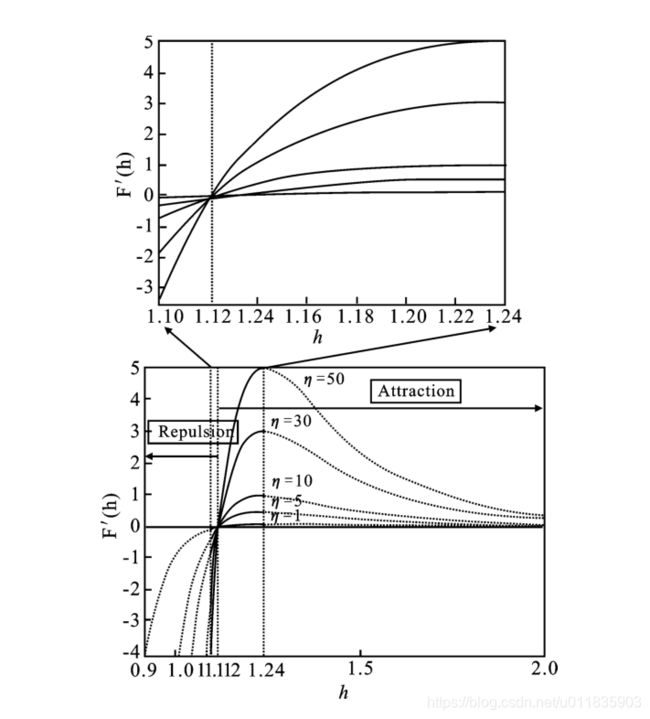
式中，$n(t)=\alpha (1-\frac{t-1}{t_{max}}{)}^3{e}^{-20t/t_{max}}$可以调节引力区域和斥力区域的范围,$n$随着迭代次数的增加， $n$自适应递减，使得全局搜索和局部开发的范围都逐步缩小至最优值，保证了算法的收敛性；$\alpha$为深度加权；$h_{ij}(t)$为两个原子之间的距离，不同的$h$值对应着不同的作用力性质 ． 如图 1 所示，当$h\in (0.9,1.1)$时为斥力，且随着$h$值得增大而增大；当h为1.12时，为平衡状态，作用力为0；当$h\in (1.12,1.24)$时，为吸引力且随着$h$值得增大而增大,$h\in (1.24,2)$时，仍为吸引力但随着$h$值得增大而减小至０ ，所以$h$可以表示为：
$$h_{ij}(t)=\{\begin{array}{l}{h}_{min},r_{ij}(t)/\sigma (t)<h_{min}\\ r_{ij}(t)/\sigma (t),h_{min}\le r_{ij}(t)/\sigma (t)\le h_{max}\\ h_{max},r_{ij}(t)/\sigma (t)>h_{max}\end{array}\text{\hspace{1em}(4)}$$
式中,$h_{min}={\epsilon }_0+\epsilon (t)$为$h$的下界,$\epsilon (t)$为漂移因子随着迭代次数的变化而变化，使得算法在全局搜索和局部开发中转换;$h_{max}$为$h$上界；$\sigma (t)=||X_{ij}(t),{\sum }_{j\in K_{best}}{X}_{ij}(t)/K(t)|{|}_2$,是$K_{best}$集合中的原子与第$i$个原子的距离范围.

图2.原子群相互作用示意图（Ｋ＝５）

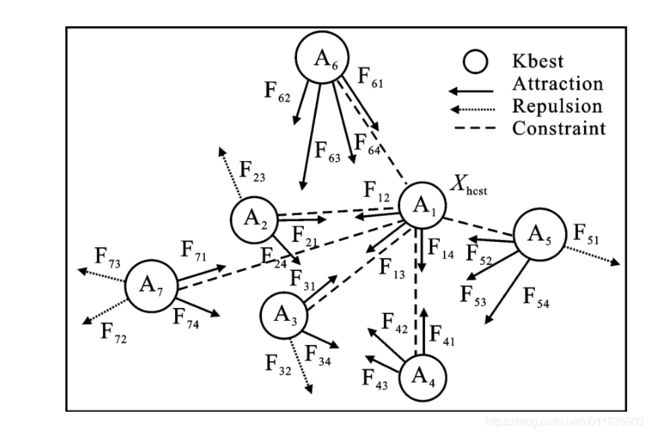
在ASO算法中，为了加强迭代初期的全局探索能力，每个原子需要与较多个适应度较好的邻近原子产生相互作用，而在迭代后期为了增强局部开发促进算法收敛，每个原子需要与较少的适应度较好的邻近原子产生相互作用 ． 适应度较好的邻近原子的数量用$K$表示,$K=s-(s-2)\ast \sqrt{t/t_{max}}$,随着迭代次数自适应减小，既保证了迭代前期算法跳出局部最优进行全局搜索的能力，又保证了算法后期局部开发能力并保证算法的收敛性 .$K_{best}$为适应度函数值较好的 ｋ 个原子的集合，原子群的作用力如图2所示．

在分子动力学模型中，几何约束在原子运动中是十分重要的因素．在ASO中，为了简单起见，假设每个原子与最优原子具有共价键，因此每个原子受来自最佳原子的约束力的作用，所以(1)式中的$G_i^d(t)$为第$t$次迭代时$d$维空间中全局最优原子对第$i$个原子的几何约束作用，表示为：
$$G_i^d(t)=\lambda (t)(X_{best}^d(t)-X_i^d(t))\text{\hspace{1em}(5)}$$
式中,$\lambda (t)=\beta e^{-20t/t_{max}}$,随着迭代次数做自适应调整；$\beta$为乘数权重 ．

(1) 式中$m_i^d(t)$为原子的质量，可表示为：

$$m_i^d(t)=M_i(t)/\sum _{j=1}^N{M}_j(t)\text{\hspace{1em}(6)}$$

$$a_i^t(t)=F_i^d(t)/m_i^d(t)+G_i^d(t)/m_i^d(t)=-\alpha (1-\frac{t-1}{t_{max}}{)}^3{e}^{-20t/t_{max}}\sum _{j\in K_{best}}\frac{randj[2(h_{ij}(t){)}^{1}3-(h_{ij}(t){)}^7]}{m_i(t)}\text{\hspace{1em}(7)}$$

加速度使得原子运动速度及位移发生变化，这便是ASO算法的位置更新的核心过程，表示为：
$$v_i^d(t+1)=ran{d}_i^d{v}_i^d(t)+a_i^d(t)\text{\hspace{1em}(8)}$$

$$X_i^d(t+1)=X_i^d(t)+v_i^d(t+1)\text{\hspace{1em}(9)}$$

算法流程：

Step1：初始化ASO各参数如种群规模，最大迭代次数等

Step2：对原子种群进行初始化

Step3：根据目标函数计算每个个体的适应度函数值，并保留为当前的最优值及最优解；

Step4：根据公式（7）更新原子运动加速度；

Step5：根据公式（8）更新原子运动速度；

Step6：根据公式（9）更新原子个体位置；

Step7：再次计算种群个体的适应度函数值，根据适应度值的优劣来更新最优解和最优值；

Step8: 重复步骤4-8 ，直到达到最大迭代次数时终止操作；

Step9: 输出最优个体位置以及最优适应度值；

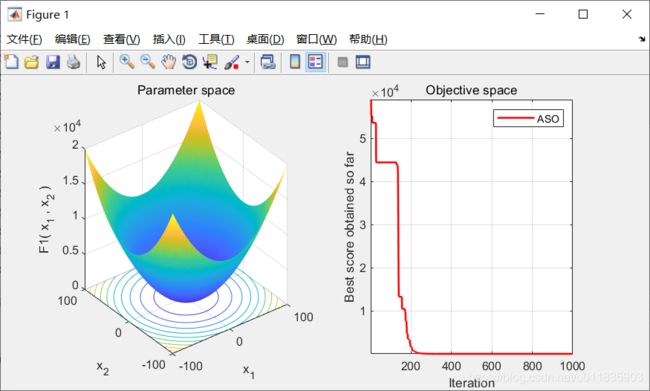
2.实验结果

3.参考文献

[1]Weiguo Zhao,Liying Wang,Zhenxing Zhang. A novel atom search optimization for dispersion coefficient estimation in groundwater[J]. Future Generation Computer Systems,2019,91.

[1]肖子雅,刘升.黄金正弦混合原子优化算法[J].微电子学与计算机,2019,36(06):21-25+30.

4.Matlab代码

改进算法matlab代码

名称	说明或者参考文献
一种改进的原子搜索算法(IASO)	[1]李建锋,卢迪,李贺香.一种改进的原子搜索算法[J/OL].系统仿真学报:1-13[2021-05-06].http://kns.cnki.net/kcms/detail/11.3092.V.20210409.1508.008.html.

算法相关应用

名称	说明或者参考文献
原子搜索算法优化的BP神经网络（预测）	https://blog.csdn.net/u011835903/article/details/112149776（原理一样，只是优化算法用原子搜索算法）
基于Tent混沌映射改进的原子搜索算法ASO优化BP神经网络（预测）	https://blog.csdn.net/u011835903/article/details/112149776（原理一样，只是优化算法用原子搜索算法）
基于Logistic混沌映射改进的原子搜索算法ASO优化BP神经网络（预测）	https://blog.csdn.net/u011835903/article/details/112149776（原理一样，只是优化算法用原子搜索算法）

个人资料介绍