【数据结构】快排的详细讲解
目录:
介绍
一,递归快排确定基准值
二,递归遍历
三,非递归的快排
四,快排的效率
介绍
快排是排序算法中效率是比较高的,快排的基本思想是运用二分思想,与二叉树的前序遍历类似,将数据划分,每次划分确定1个基准值(就是已经确定好有序后位置的数据),以升序为例,基准值左面的数据都比此值小,右面的数据都比此值大,然后以基准值为分界线,经过不断划分,最终基准值的个数达到n,数据即有序,因此,递归运用是不二选法,也可运用非递归,但是比较麻烦。
一,递归快排确定基准值
确定基准值的方法常用的有三种,普通法,挖坑法,前后指针法。
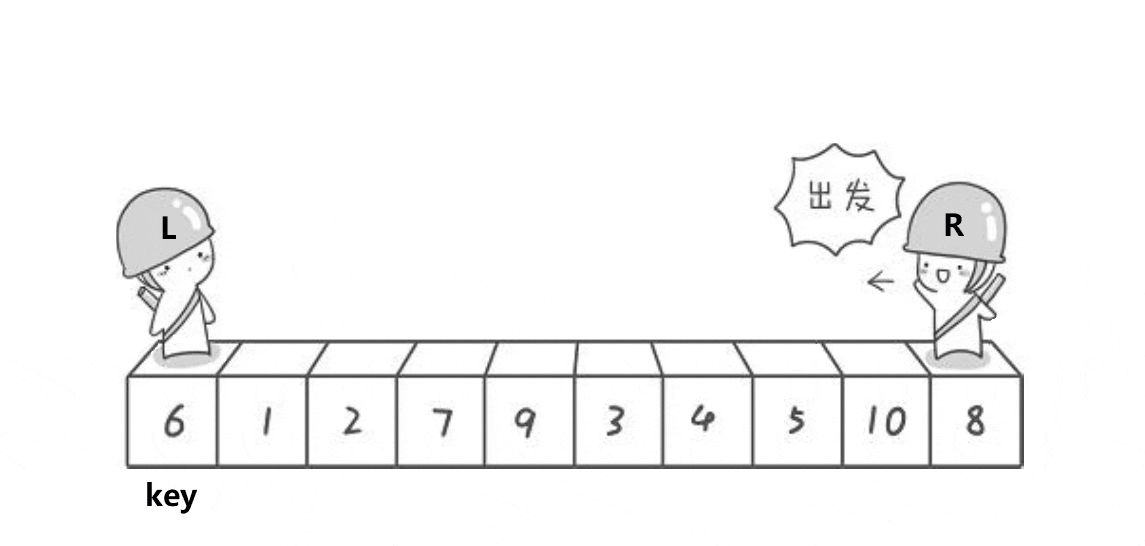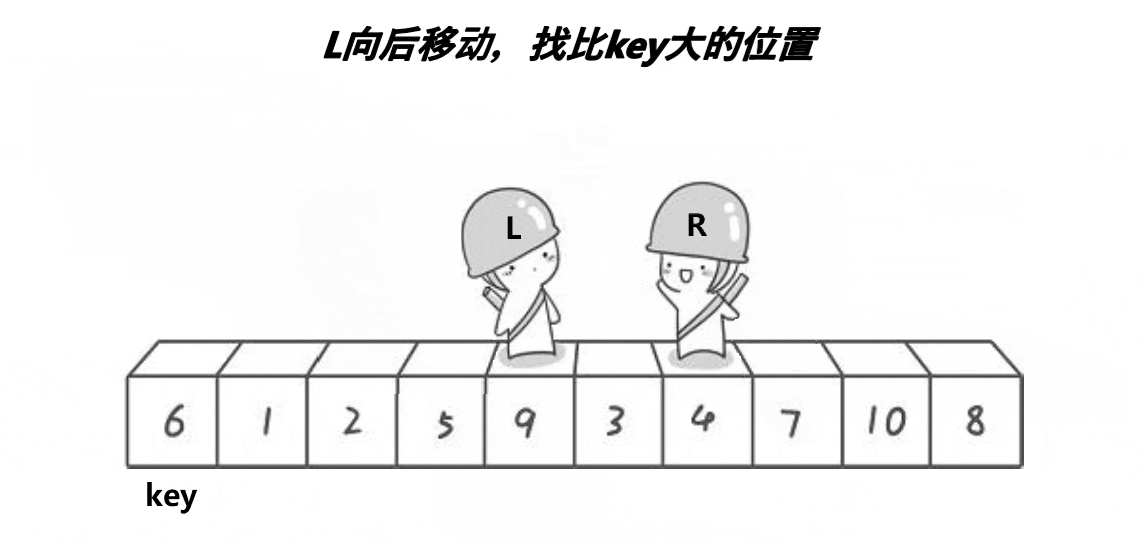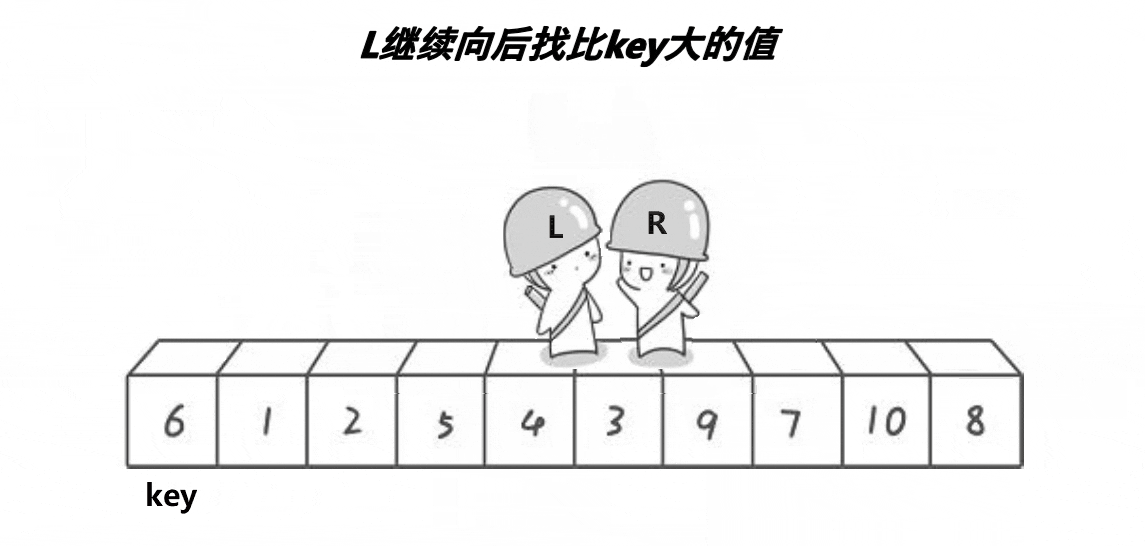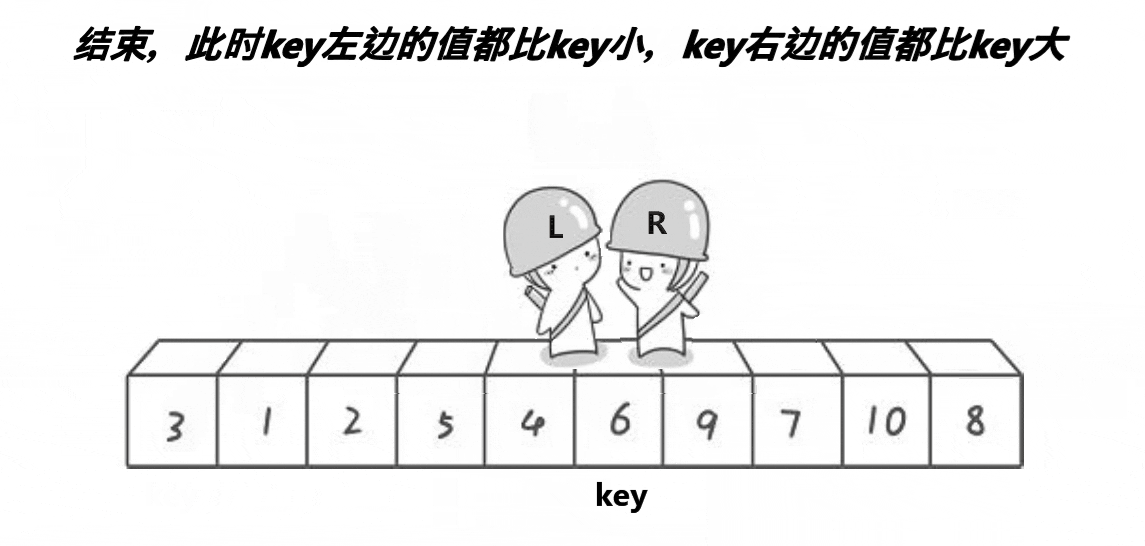
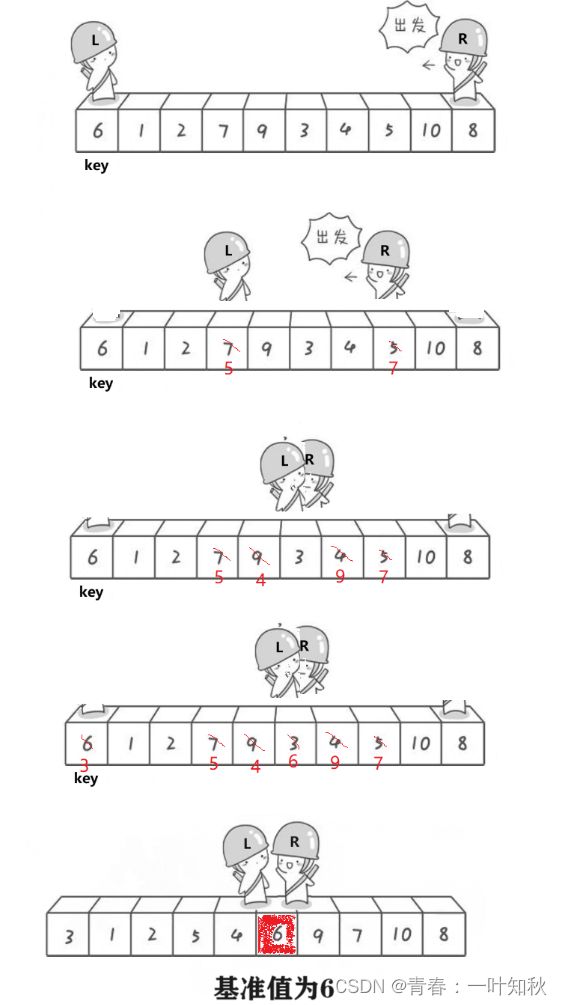
1,普通法,具体思想图如下(以升序为例):
上面说过,基准值的确定过程要保证左面的数据都比此值小或大,右面的数据都要比此值大或小,因此,此基准值就确定了在整个数据中的位置。以升序为例,我们可以从开头和末尾遍历数据,比开头(以首元素为基准)元素大的放在最后,比开头元素小的数据放在前面,最终当两者相遇后再与开头元素交换即可确定基准值(注意:此步骤有细节,具体后面会说明)。如下图:
基准值过程图
现在有个注意要素套提一下,当上图中的前面L和后面R相遇时,如何保证此值一定比首元素小呢?这里我们需要控制好L的走向即可,即让R先走,当遇见比首元素小时退出,然后让L走,最后让两者进行交换,这样一来无论出现什么情况,当L与R相遇时对应的数据将一定比首元素(即以第一个元素为基准)小,此步骤称为预排序。
基准值的确定代码如下:
void Swap(int* x1, int* x2) {
int t = *x1;
*x1 = *x2;
*x2 = t;
}int PartSort1(int* a, int begin, int end) {
int key = begin;
while (begin < end) {
//注意此步骤,end必须先开始(即当左边开始行走右边一定有比key小的值),
//因为要控制最后的begin最终比key(开头元素)小,因此,右边必须先走.
while (begin < end && a[end] >= a[key]) {
end--;
}
//当走左边时,最终会Swap(a + end, a + begin);交换后begin的最终比key小
while (begin < end && a[begin] <= a[key]) {
begin++;
}
Swap(a + end, a + begin);
}
Swap(a + key, a + begin);
return begin;
}
2,挖坑法,原理图如下(以升序为例):
挖坑发大致思想与普通法一样,不同的是挖坑发有了坑位。挖坑发是先将首元素保存,将此位置形成坑位(其实坑位上有数据,但坑位的数据不影响,为了方便理解,所以在上图中的坑位就没写上去),然后开始首尾遍历(尾要先遍历,原理同上),比key大的元素放在后面,比key小的元素放在前面,一旦不满足此情况,这个数据将给到位置L或位置R,原本的位置将会形成坑位,直到两者相遇为止,结束遍历,最后把key的值放入坑位即可。代码如下:
int PartSort2(int* a, int begin, int end) {
int key = a[begin];
int hole = begin;//开头先形成坑位
while (begin < end) {
// 右边先走(原理与PartSort1原理一样),找小,填到左边的坑,右边形成新的坑位
while (begin < end && a[end] >= key) {
end--;
}
a[hole] = a[end];
hole = end;
// 左边再走,找大,填到右边的坑,左边形成新的坑位
while (begin < end && a[begin] <= key) {
begin++;
}
a[hole] = a[begin];
hole = begin;
}
a[hole] = key;
return hole;
}
3,前后指针法(prev是前指针,cur是后指针,此指针是位置指针,不是我们所常说的指针型),原理图如下:
前后指针法跟上面两种方法有很大不同,如上,以第一个元素为基准,即定义key值为首元素,cur往前遍历,prev随之跟上cur的步伐,当prev遇到的数据比key小,prve向前移动;当prev遇到的数据比key大,prev停止移动,此时,cur不断向前移动,一旦找到比key小的数据就会跟prev指向的数据进行交换,最后,当cur遍历完整个数据后cur与key会进行交换,确定此时key所对应的值比左边数据大,比右边数据小。代码如下:
void Swap(int* x1, int* x2) {
int t = *x1;
*x1 = *x2;
*x2 = t;
}
int PartSort3(int* a, int begin, int end) {
int front = begin + 1;
int back = begin;
while (front <= end) {
if (a[front] <= a[begin]) {
back++;
Swap(a + back, a + front);
}
front++;
}
//因为后指针控制,所以当程序结束后back所指向的数据都比keyi所指向的数据小
Swap(a + begin, a + back);
return back;
}
总:以上三种遍历确定基准值的方法在快排称为预排序,每一趟预排序都可确定数据中一个元素的排序位置,每当确定一个数据后相对位置后,我们只需要不断以上次遍历时确定的基准值为界,递归遍历数据,即可确定最终确定序列。
二,递归遍历
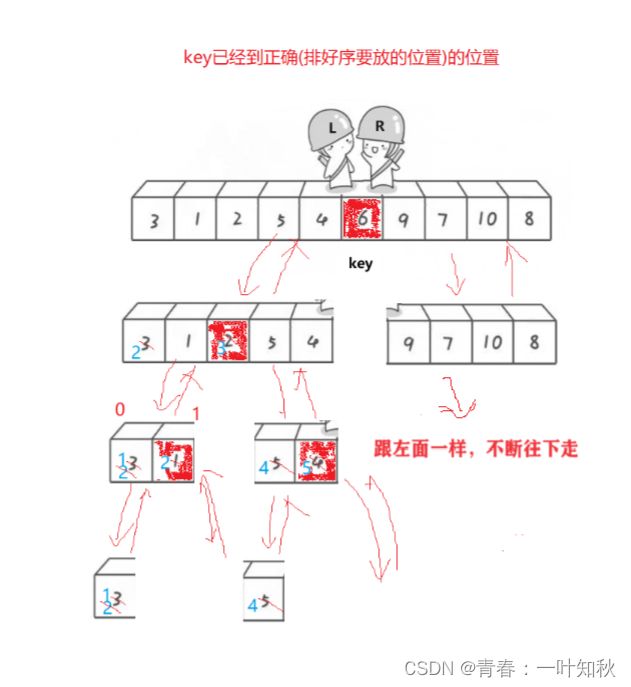
当我们明白如何确定基准值后,接下来就是程序的结构搭建了,上面说过,快排递归跟二叉树的前序遍历一样,并且还需要以基准值为分界线,不断确定基准值,具体思路导图如下:
当确定好基准值key后,以区间[begin, key - 1]和区间[key + 1, end]进行划分(begin是要进行遍历时,开头元素的坐标,end是要遍历时,结尾元素的坐标,如上图),以次区间不断进行与二叉树前序遍历相同的递归,根据上图所示,很明显,当begin>=end时结束下一层递归。代码如下:
void QuickSort(int* a, int begin, int end)
{
//即当不存在区间时结束,即就排好了一个数
if (begin >= end)
return;
//运用普通法PartSort1,此算法是返回一个顺序表中中间值的坐标,在坐标左边都小于此数,在坐标的右边都大于此数
int keyi = PartSort1(a, begin, end);//也可用挖坑法和前后指针法
// 区间递归: 以keyi为界,左[begin, keyi-1],右[keyi+1, end],一直缩小,最终会逐渐会缩小成有序
QuickSort(a, begin, keyi - 1);//在keyi的左面进行遍历
QuickSort(a, keyi + 1, end);//在keyi的右面进行遍历
}
下面是总代码:
#include
void Swap(int* x1, int* x2) {
int t = *x1;
*x1 = *x2;
*x2 = t;
}
int PartSort1(int* a, int begin, int end) {
int key = begin;
while (begin < end) {
//注意此步骤,end必须先开始(即当左边开始行走右边一定有比key小的值),
//因为要控制最后的begin最终比key(开头元素)小,因此,右边必须先走.
while (begin < end && a[end] >= a[key]) {
end--;
}
//当走左边时,最终会Swap(a + end, a + begin);交换后begin的最终比key小
while (begin < end && a[begin] <= a[key]) {
begin++;
}
Swap(a + end, a + begin);
}
Swap(a + key, a + begin);
return begin;
}
void QuickSort(int* a, int begin, int end)
{
//即当不存在区间时结束,即就排好了一个数
if (begin >= end)
return;
//PartSort1算法是返回一个顺序表中中间值的坐标,在坐标左边都小于此数,在坐标的右边都大于此数
int keyi = PartSort1(a, begin, end);
// 区间递归: 左[begin, keyi-1] keyi 右[keyi+1, end],一直缩小,最终会逐渐会缩小成排序
QuickSort(a, begin, keyi - 1);//在keyi的左面进行遍历
QuickSort(a, keyi + 1, end);//在keyi的右面进行遍历
}
void Print(int* a, int n) {
for (int i = 0; i < n; i++) {
fprintf(stdout, "%d ", a[i]);
}
puts("");
}
void TestQuickSort()
{
int a[] = { 6,1,2,7,9,3,4,5,10,8 };
QuickSort(a, 0, sizeof(a) / sizeof(int) - 1);
Print(a, sizeof(a) / sizeof(int));
}
int main() {
TestQuickSort();
return 0;
} 运行图:
三,非递归的快排
运用非递归,大多数要运用栈结构,因为递归本身其实就是不断入栈和出栈,递归过程跟栈结构一样,进入递归就是入栈,出函数就是出栈,都是先进后出。快排的非递归实现,我们也可用栈来实现。根据前面递归的运用,递归是不断进行区间分割,我们可将此区间放入栈中,然后进行不断循环遍历,每当遍历时就将区间放入栈中,一旦用完此区间就释放,跟递归中函数栈帧的创建与销毁一样。非递归结构代码如下:
1,栈的建立
typedef struct stack {
int* Data;
int Capacity;
int Top;
}Stack;
//以下三个是要运用栈结构的算法
void StackInit(Stack* S);
void StackPop(Stack* S);
void StackPush(Stack* S, int X);
//栈功能的实现
void StackInit(Stack* S) {//初始化栈
assert(S);
S->Data = 0;
S->Capacity = 0;
S->Top = -1;
}
void StackPop(Stack* S) {//出栈
assert(S || S->Data || S->Top != -1);
S->Top--;
}
void StackPush(Stack* S, int X) {//入栈
assert(S);
if (!S->Data) {
S->Data = (int*)malloc(sizeof(int) * 4);
assert(S->Data);
S->Capacity = 4;
}
else if (S->Top == S->Capacity - 1) {
S->Data = (int*)realloc(S->Data, (sizeof(int) * S->Capacity) * 2);
assert(S->Data);
S->Capacity *= 2;
}
S->Data[++S->Top] = X;
}
2,非递归的结构
void QuickSort(int* a, int left, int right) {
//创建栈结构S,以栈来模仿递归过程
Stack* S = (Stack*)malloc(sizeof(Stack));
StackInit(S);
StackPush(S, right);
StackPush(S, left);
while (S->Top != -1) {
//确定左右区间,每当遍历完一次时要及时更换,即从栈中去除操作
int begin = S->Data[S->Top];
StackPop(S);
int end = S->Data[S->Top];
StackPop(S);
//用指定好的区间进行预排序,即一次遍历
int key = PartSort1(a, begin, end);
//进行左区间的遍历
if (end - 1 > begin) {
//注意栈结构先进后出的特点,要先把end装进去
StackPush(S, end - 1);
StackPush(S, begin);
}
//进行右区间的遍历
if (begin + 1 < end) {
//同理,要先把end装进去
StackPush(S, end);
StackPush(S, begin + 1);
}
}
free(S);
//注意,不能在此算法内这样写,因为这是的a是首元素地址,即指针,sizeof(a)为地址的大小
//Print(a, sizeof(a) / sizeof(int));
}
以上是非递归过程中的逻辑代码,除此两大步,其它的逻辑运用与递归无任何区别,总代码如下:
#include
#include
#include
typedef struct stack {
int* Data;
int Capacity;
int Top;
}Stack;
//以下三个是要运用栈结构的算法
void StackInit(Stack* S);
void StackPop(Stack* S);
void StackPush(Stack* S, int X);
//栈功能的实现
void StackInit(Stack* S) {//初始化栈
assert(S);
S->Data = 0;
S->Capacity = 0;
S->Top = -1;
}
void StackPop(Stack* S) {//出栈
assert(S || S->Data || S->Top != -1);
S->Top--;
}
void StackPush(Stack* S, int X) {//入栈
assert(S);
if (!S->Data) {
S->Data = (int*)malloc(sizeof(int) * 4);
assert(S->Data);
S->Capacity = 4;
}
else if (S->Top == S->Capacity - 1) {
S->Data = (int*)realloc(S->Data, (sizeof(int) * S->Capacity) * 2);
assert(S->Data);
S->Capacity *= 2;
}
S->Data[++S->Top] = X;
}
void Swap(int* x1, int* x2) {
int t = *x1;
*x1 = *x2;
*x2 = t;
}
int PartSort1(int* a, int begin, int end) {
int key = begin;
while (begin < end) {
//注意此步骤,end必须先开始(即当左边开始行走右边一定有比key小的值),
//因为要控制最后的begin最终比key(开头元素)小,因此,右边必须先走.
while (begin < end && a[end] >= a[key]) {
end--;
}
//当走左边时,最终会Swap(a + end, a + begin);交换后begin的最终比key小
while (begin < end && a[begin] <= a[key]) {
begin++;
}
Swap(a + end, a + begin);
}
Swap(a + key, a + begin);
return begin;
}
void QuickSort(int* a, int left, int right) {
//创建栈结构S,以栈来模仿递归过程
Stack* S = (Stack*)malloc(sizeof(Stack));
StackInit(S);
StackPush(S, right);
StackPush(S, left);
while (S->Top != -1) {
//确定左右区间,每当遍历完一次时要及时更换,即从栈中去除操作
int begin = S->Data[S->Top];
StackPop(S);
int end = S->Data[S->Top];
StackPop(S);
//用指定好的区间进行预排序,即一次遍历
int key = PartSort1(a, begin, end);
//进行左区间的遍历
if (end - 1 > begin) {
//注意栈结构先进后出的特点,要先把end装进去
StackPush(S, end - 1);
StackPush(S, begin);
}
//进行右区间的遍历
if (begin + 1 < end) {
//同理,要先把end装进去
StackPush(S, end);
StackPush(S, begin + 1);
}
}
free(S);
//注意,不能在此算法内这样写,因为这是的a是首元素地址,即指针,sizeof(a)为地址的大小
//Print(a, sizeof(a) / sizeof(int));
}
void Print(int* a, int n) {
for (int i = 0; i < n; i++) {
fprintf(stdout, "%d ", a[i]);
}
puts("");
}
int main() {
int a[] = { 0,5,7,9,3,4,1,6,2,8 };
QuickSort(a, 0, sizeof(a) / sizeof(int) - 1);
Print(a, sizeof(a) / sizeof(int));
return 0;
} 运行图:
四,快排的效率
1,快排的效率分析
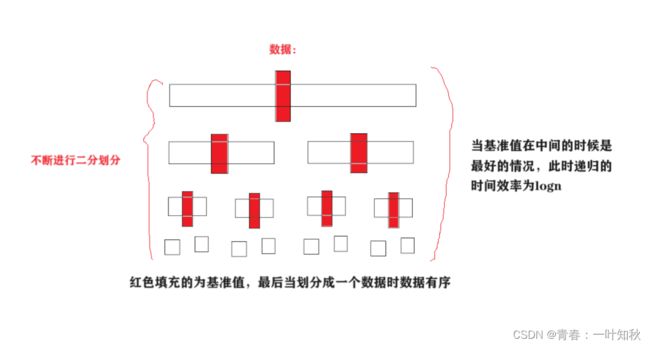
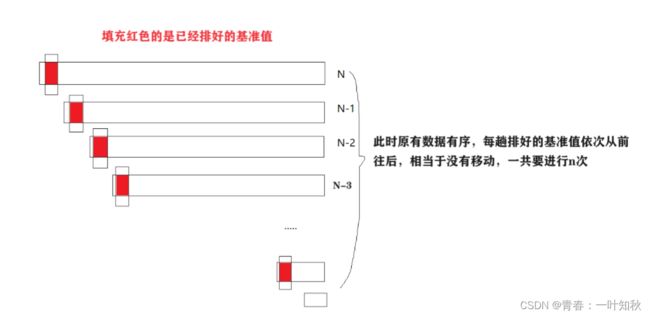
快排效率在平常说是效率比较高的,大致根据二叉树原理计算,快排时间复杂度为O(nlogn),空间复杂度为O(logn),但这只是对于大多时候,其实快排的时间效率是很不确定的,快排的效率跟数据的原有序列有关,序列越接近有序,快排效率越低。我们先观察以下图:
快排效率最好情况
快排效率最坏情况
可知,快排预排序的时间效率在区间[logn,n],当原有序列越有序时,无论是递归还是非递归时间效率都很低,有序时效率最低,而遍历元素的时间复杂度不变,一直是O(n),因此快排的时间效率在区间[nlogn,n^2]。
2,三数取中
当快排在有序时(升序为例),数据会靠近左边进行排序,而要想提高快排的效率,就必须尽量让基准值尽量往中间靠拢,但这样很难控制,因为这与数据原有的序列有关。虽然说我们不能直接控制,但是我们可控制最坏情况来进而控制时间效率,即序列有序时的情况。
通常,我们是选取首元素为基准值的,因此,只要控制好首元素不为基准值的情况即可,也就是三数取中。
三数取中是将判断首元素,尾元素,中间元素三者之间的大小,将中间大的数据与首元素交换,使首元素不可能为基准值。代码如下:
int GetMidi(int* a, int left, int right)
{
int mid = (left + right) / 2;//中间数mid
//下面比较 left mid right 三者之间大小,将中间大的数据的下标返回过去
//先人left与mid比较,然后进一步判断right
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right]) // mid是最大值
{
return left;
}
else
{
return right;
}
}
else
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right]) // mid是最小
{
return left;
}
else
{
return right;
}
}
}
具体思想就是先两两比较,然后进一步与第三者比较,上面代码中选举了left与mid两者之间比较,然后再跟第三者right比较,满足中间大的数据返回其下标。
3,改善后算法的运用
有了三数取中,快排将不会出现最坏情况,虽说有可能会出现次坏情况,但基本是不可能的,因为这种情况很是要求原序列的次序和三数取中的交换,因次,如若在算法中加上三数取中后算法的时间复杂度基本为O(nlogn)。下面是改进后运用的代码:
int GetMidi(int* a, int left, int right)
{
int mid = (left + right) / 2;//中间数mid
//下面比较 left mid right 三者之间大小,将中间大的数据的下标返回过去
//先人left与mid比较,然后进一步判断right
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right]) // mid是最大值
{
return left;
}
else
{
return right;
}
}
else
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right]) // mid是最小
{
return left;
}
else
{
return right;
}
}
}
void Swap(int* x1, int* x2) {
int t = *x1;
*x1 = *x2;
*x2 = t;
}
//普通法
int PartSort1(int* a, int begin, int end) {
//运用三数取中,与每次预排序的区间首元素交换,防止出现最坏情况
int midi = GetMidi(a, begin, end);
Swap(a + begin, a + midi);
//以下代码正常不变
int key = begin;
while (begin < end) {
//注意此步骤,end必须先开始(即当左边开始行走右边一定有比key小的值),
//因为要控制最后的begin最终比key(开头元素)小,因此,右边必须先走.
while (begin < end && a[end] >= a[key]) {
end--;
}
//当走左边时,最终会Swap(a + end, a + begin);交换后begin的最终比key小
while (begin < end && a[begin] <= a[key]) {
begin++;
}
Swap(a + end, a + begin);
}
Swap(a + key, a + begin);
return begin;
}
//挖坑发
int PartSort2(int* a, int begin, int end) {
//运用三数取中,与每次预排序的区间首元素交换,防止出现最坏情况
int midi = GetMidi(a, begin, end);
Swap(a + begin, a + midi);
//以下代码正常不变
int key = a[begin];
int hole = begin;//开头先形成坑位
while (begin < end) {
// 右边先走(原理与PartSort1原理一样),找小,填到左边的坑,右边形成新的坑位
while (begin < end && a[end] >= key) {
end--;
}
a[hole] = a[end];
hole = end;
// 左边再走,找大,填到右边的坑,左边形成新的坑位
while (begin < end && a[begin] <= key) {
begin++;
}
a[hole] = a[begin];
hole = begin;
}
a[hole] = key;
return hole;
}
//前后指针法
int PartSort3(int* a, int begin, int end) {
//运用三数取中,与每次预排序的区间首元素交换,防止出现最坏情况
int midi = GetMidi(a, begin, end);
Swap(a + begin, a + midi);
//以下代码正常不变
int front = begin + 1;
int back = begin;
while (front <= end) {
if (a[front] <= a[begin]) {
back++;
Swap(a + back, a + front);
}
front++;
}
//因为后指针控制,所以当程序结束后back所指向的数据都比keyi所指向的数据小
Swap(a + begin, a + back);
return back;
}
在以上中,除了预排序算法需要改进,其它的都不用动即可实现高效的快排。最后,跟大家再次强调一下快排的效率,快排在大多数情况下确实效率很高,但快排的效率受原数据的序列影响比较大,当序列越接近有序时,快排的效率可能还没有其它算法高,在以后的运用中要不要用快排还需根据原数据的情况而定。