【数据结构】——快排详解
文章目录
- 1、快排的含义
- 2、快排的实现
-
- 2.1思路讲解
- 2.2代码实现
- 3、快排的时间复杂度分析
- 4、快排的优化
上一篇文章我们介绍了八大排序中的七种,今天这篇文章主要来详细介绍一种比较重要也是常用的一种排序算法——快速排序~
1、快排的含义
快速排序是一种二叉树结构的交换排序方法。相当于是冒泡排序的一种升级,都是属于交换排序类,通过不断比较和移动交换来实现排序。
其基本思想是:任意取待排序元素序列中的某个元素作为基准值,按照这个排序码把待排序集合分割成两个子序列
- 左子序列中所有元素都小于该基准值
- 右子序列中所有元素都大于该基准值
然后左右两边子序列又重复该过程,直到所有元素都排列在相应的位置上为止。
2、快排的实现
2.1思路讲解
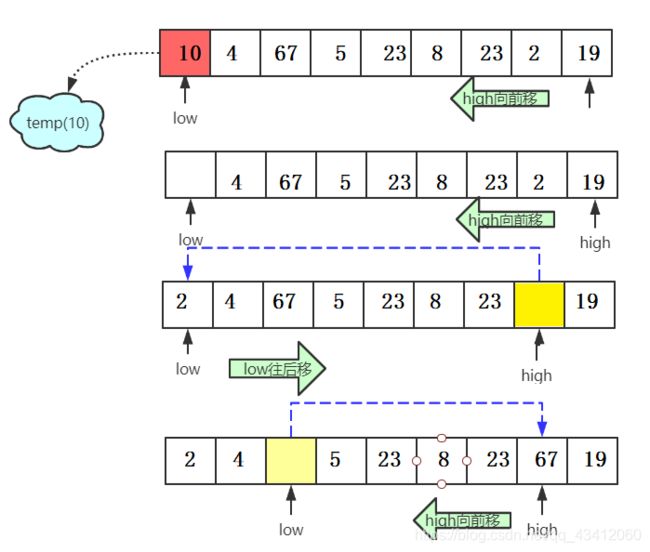
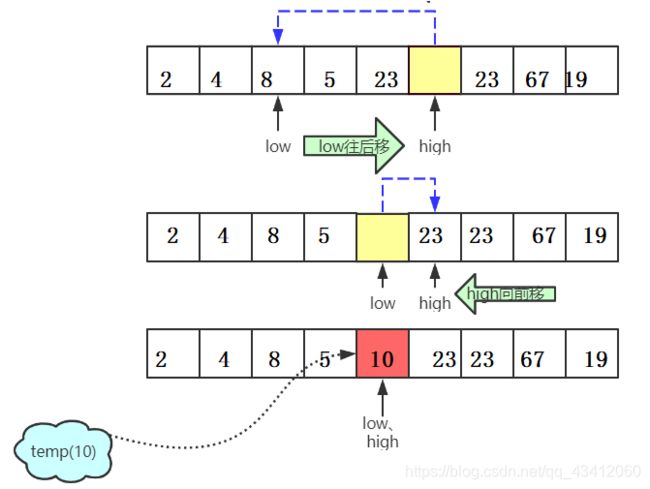
整个快排的核心就在于选取一个基准值先存放在一个临时变量里面,然后定义两个指针low和high分别指向数组的开头和末尾,并挨个儿和基准值比较。
先从数组的末尾指针high开始向前遍历,查找比基准值小的数字,找到了就将其填充到low指向的位置再调换方向,从low开始向后遍历,查找比基准值大的数字,找到了就将其填充到high指向的位置- 再次循环交替进行遍历查找填充。循环结束的条件就是两个指针都指向了同一个位置。
- 最后将临时变量存放的基准值填充到最后low指向的位置。
- 接下来的过程就是一个递归的过程,在各自的子序列里面再进行上述过程。
2.2代码实现
1、对数组作快速排序
因为要进行递归过程,所以要传出low和high指针指向的位置
void QuickSort(int* arr, int n)
{
Quick(arr, 0, n - 1);
}
2、递归函数Quick的实现
- pivot为一次划分返回的基准值
- 如果low还小于该基准值,说明一次划分后的左边还有元素,继续递归划分
- 如果high还大于该基准值同理。
void Quick(int* arr, int low, int high)
{
int pivot = Partition(arr, low, high);
if (low < pivot)
{
Quick(arr, low, pivot - 1);
}
if (pivot < high)
{
Quick(arr, pivot +1,high);
}
}
3、 Partition一次划分的过程
这段代码的核心部分是pivot = Partition(arr,low,high);使得他左边的值都比他小,右边的值都比他大。
【举个栗子】
数组值为[50,10,90,30,70,40,80,60,20]经过Partition(L,0,8)执行后,数组变成{20,10,40,30,50,70,80,60,90},并返回值4给pivot,然后递归调用QSort(L,1,4-1)QSort(L,4+1,9)语句,其实就是在对{20,10,40,30}{70,80,60,90}分别进行同样的Partition操作,直到顺序全部正确为止。
int Partition(int* arr, int low, int high)
{
int temp = arr[low];
while (low < high)
{
while (low < high && arr[high] >= temp)
{
high--;
}
arr[low] = arr[high];
while (low < high && arr[low] <= temp)
{
low++;
}
arr[high] = arr[low];
}
arr[low] = temp;
return low;
}
还有另外一种思路参见博客快排详解
整体实现如下:
#include3、快排的时间复杂度分析
快排的时间性能取决于快排递归的深度。可以用递归树来描述递归算法的执行情况。如果排序n个关键字,其递归树的深度就是【log2n】+1,在最优的情况下,快速排序
- 时间复杂度是O(nlogn)
- 空间复杂度是O(logn)
4、快排的优化
1、优化选取枢轴
如果我们选取的基准值是处在整个序列的中间位置,那么我们可以将整个序列分成小数集合和大数集合。但是,假如我们选取的pivotkey不是中间数又如何呢?——可能导致整个系列没有一个实质性的变化。所以temp =arr[low];变成了一个潜在的性能瓶颈。
1.1随机化法获取基准值
使用随机树种子产生一个随机值pos下标。先让该下标所指向位置的值和数组的首元素交换,最后还是确定首元素为基准值。
只需要将partition函数的temp = arr[low];语句修改如下:
int pos = rand() % (high - low + 1) + low;
int temp = arr[pos];
arr[pos] = arr[low];
arr[low] = temp;
temp = arr[low];
1.3三数取中法
但是还是会存在数据可能是随机的有序的情况,所以我们针对于随机选取基准点的方法还做出了优化,采用三数取中的方法:把low,mid,high所指的三个数据中,把中间大的数据放在最左边开始位置。
在上面快排代码的基础上进行增加改进的代码实现如下:
void Swap(int arr[], int first, int second)
{
int temp = arr[first];
arr[first] = arr[second];
arr[second] = temp;
}
void GetMiddleMaxNum(int arr[], int low, int mid, int high)
{
if (arr[mid] > arr[high])
{
Swap(arr, mid, high);
}
if (arr[low] < arr[high])
{
Swap(arr, low, high);
}
if (arr[low] > arr[mid])
{
Swap(arr, low, mid);
}
}
void Quick(int* arr, int low, int high)
{
int mid = (low + high) / 2;
GetMiddleMaxNum(arr, low, mid, high);
int pivot = Partition(arr, low, high);
if (low < pivot)
{
Quick(arr, low, pivot - 1);
}
if (pivot < high)
{
Quick(arr, pivot +1,high);
}
}
2、优化不必要的交换
我们发现,50这个关键字,其位置变化是1->9->3->6->5,可其实他的最终目标是5,当中的交换其实是不需要的。
所以我们对此进行优化:
int Partition(SqList *L,int low,int high)
{
int pivotkey;
//这里省略三数取中代码
pivotkey = L->r[low];
L->r[0] = pivotkey;//将枢轴关键字备份到L->r[0]
while(low < high)
{
while(low < high && L->r[high] >= pivotkey)
high--;
L->r[low] = L->r[high];//采用替换而不是交换的方式进行操作
while(low < high && L->r[low] <= pivotkey)
low++;
L->r[high] = L->r[low];
}
L->r[low] = L->r[0];
return low;//返回枢轴所在位置
}
3、优化小数组时的排序方案
如果数组非常小的情况下,快速排序反而不如直接插入排序来得更好(直接插入排序是简单排序中性能最好的)。
因此改进QSort函数代码实现如下:
void InsertSort(int* arr, int low,int high)
{
int i, j, temp;
for (i = low+1; i <= high; i++)
{
temp = arr[i];
for (j = i - 1; j >= low && arr[j] > temp; j--)
{
arr[j + 1] = arr[j];
}
arr[j + 1] = temp;
}
return;
}
void Qsort(int* arr, int low, int high)
{
int pivot;
while (low < high)
{
if ((high - low) < 20)
{
InsertSort(arr, low, high);
}
pivot = Partition(arr, low, high);
Qsort(arr, low, pivot - 1);
Qsort(arr, pivot + 1, high);
}
}
4、优化递归操作
递归对性能有一定影响,栈的大小是有限的,每一次递归调用都会耗费一定的栈空间,函数的参数越多,每次递归耗费的口空间也越多。
对QSort实施尾递归优化:
#define MAX_LENGTH_INSERT_SORT 7
void QSort(sqList *L,int low,int high)
{
int pivot;
//当high-low大于常数时用快排
if((high - low) > MAX_LENGTH_INSERT_SORT)
{
while(low<high)
{
pivot = Partition(L,low,high);
QSort(L,low,pivot-1);
low = pivot + 1;
}
}
else
InsertSort(L);
}
将if改成while后,因为第一次递归以后,变量low就没有用处了,所以可以将pivot + 1的值赋值给low,再循环后Partition(L,low,high)的效果等同于Partition(L,pivot + 1,high)。
因此采用迭代而不是递归的方法可以缩减堆栈深度,从而提高了整体性能。