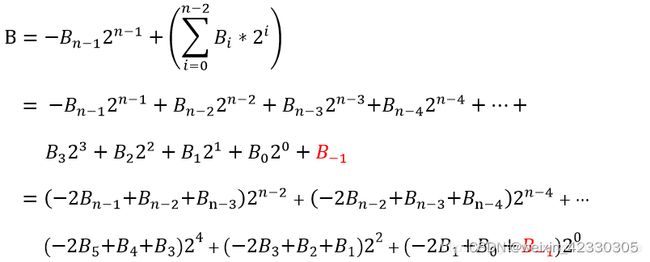booth乘法器的原理与verilog实现

​
一、乘法原理

如图所示，二进制乘法和十进制乘法类似，都是单bit相乘，移位后相加
​​​​​​
如a(4bit)*b(4bit)

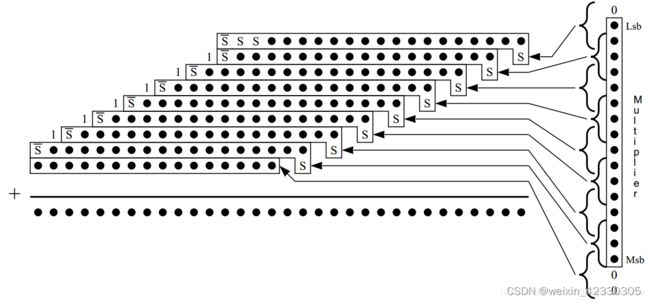
将上图中所有数相加时，我们会用到阵列乘法器

其中，HA表示半加器，FA表示全加器，虚线表示进位链
上图红色和紫色线表示最长路径，代表了组合逻辑深度，我们对其进行优化

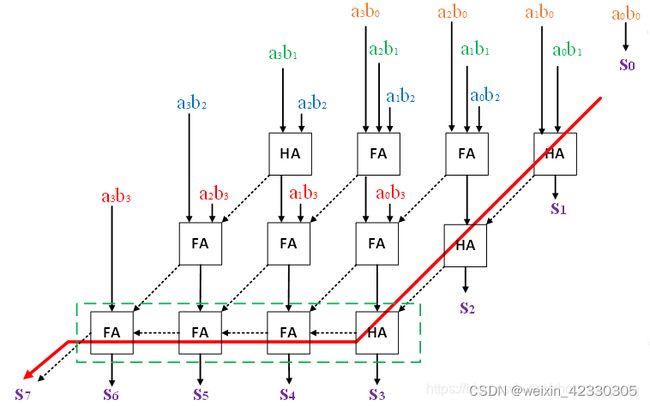
优化后，进位链变短
由此我们可以得出，乘法运算由2部分组成：生成部分积、通过加法树对数据压缩
二、部分积生成

如图所示，红框中的数即为部分积
我们知道，01110 = 10000 - 00010
因此，上述5个数相加就可化简为2个数相减
110100000-110100
减法可以用加补码表示
110100000+001100
因此，当有连续的“1”时，这种方法可以减少部分积的个数，加法树的层级变小
这就是radix编码

对于二进制有符号数，其二进制好十进制的转化方法为：

1、Radix-2编码
B可以展开为：

A*B可以写为：

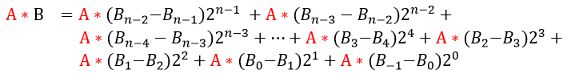
Radix-2编码可以消除2bit连续的“1”，但是对于硬件电路来说，加法树的层级并没有得到减少，反而引入了编码电路，由此引出radix-4编码

2、Radix-4编码

其基系数为：

B可以展开为：

A*B可以写为：

对每一组A、B相乘

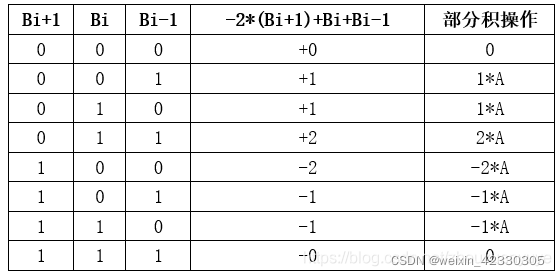
由上表可以看出，我们只需要对A进行取补码或者移位操作，就可完成部分积的计算
相比于Radix-2 Booth编码，Radix-4 Booth编码将使得乘法累积的部分和数减少一半，部分积只涉及到移位和补码计算。

3、符号位扩展

假设16*16无符号乘法器的所有部分积均为正数，除了底部的部分和为16bit，其他部分和的位宽均为17bit。

这是因为Radix-4编码是基于最高bit是符号位，所以对于1616的无符号乘法，需要对高位补0

以公式

为例，如图所示，紫色是与基系数的项，蓝色是补充的符号位
对于
来说，Bn-1、Bn-2均为0，所以基系数只可能是1或-1，因此底部的部分和为16bit，而其他的基系数的取值范围是0~2（假设均为正数），所以位宽是17bit
如图

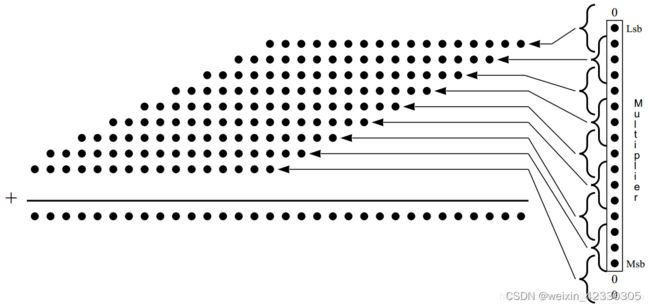
假设1616无符号乘法器的所有部分积均为负数，用二进制补码表示，需要取反，最低bit加1

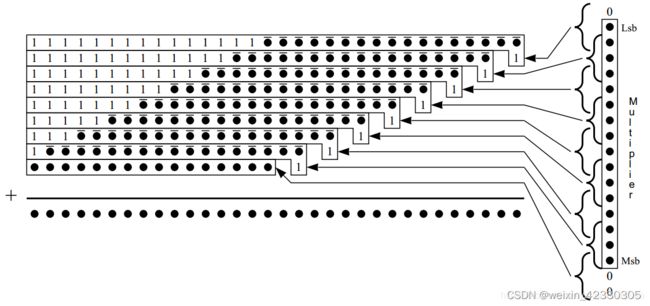
我们对高位的1进行化简，由于上图中所有的数相加后即为乘法结果，我们先将高位的1相加，结果如图

由此，部分积为正数或负数的情况我们都有了，这时候，我们需要对这两种情况进行区分
我们可以看出，两者的区别在于两个部分，一个是低位是否加1；另一个是高位扩展的2bit数的值。
对于低位加1，我们设置变量S，让低位加S，若部分积为负值，则S为1，若部分积为正值，则S为0
对于高位扩展数的值，如下图所示，若为1，则随着进位，高bit扩展位为0

为减少部分积的个数，优化为下图

以上是无符号乘法，对于有符号乘法，有以下3点不同

1、

对于16bit*16bit数，最高位第15bit即为符号位，不需要额外扩展符号位
2、对于最底部的部分积，也不能保证其取值范围了，因此也需要最低位加S，高位扩展
我们引入变量E，E为1表示被乘数与编码有相同符号位，为0则不同

二、加法树

1、Wallace树

1963年，C.S.Wallace提出的一种高效快速的加法树结构，被后人称为Wallace树。其基本思想如下在其文章中描述如下：

Assuming that all summands are generated simultaneously the best possible first step is to group the summands into threes, and introduce each group into its own pseudoadder, thus reducing the count of numbers by a factor of 1.5 ( or a little less, if the number of summands is not multiple of three). The best possible second step is to group the numbers resulting from the first step into threes and again add each group in its own pseudoadder. By continuing such steps until only two numbers remain, the addition is completed in a time proportional to the logarithm of the number of summands.

简单地讲即许多个加数求和，每3个加数分为一组，压缩至2个加数，循环往复。

但是会用到较多的半加器，半加器电路图如图所示：

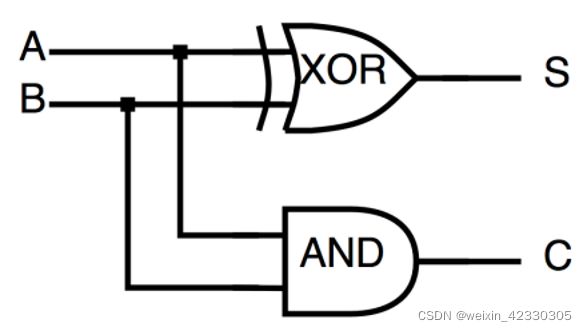
我们可以看到，其输入为2bit数，输出2bit数，对于数据的压缩没有作用，而我们加法树的最终目的是将数据压缩为2行，最后由行波进位加法器相加后即为最终结果。
因此我们需要用到尽量多的全加器：

其输入3bit，输出2bit，对数据起到了压缩的作用。
2、Dadda树

Dadda树则解决了以上问题。
Dadda tree首先从部分积的中间位进行FA累加，边角部分若不满足下层条件则不进行累加，进位会不断的补充到高位，高位部分层数会增多（部分积的图形类似平行四边形，两边层级较少），因此使用更多了FA

三、实现方法

对于基系数的生成
乘数的相关bit位和基系数的对应关系如表所示

因此

Always @ （*）    begin
    case(din)    begin
    	3'b000:    dout = 3'b000;  //+0
      	3'b001:    dout = 3'b001;  //+1
      	3'b010:    dout = 3'b001;  //+1
      	3'b011:    dout = 3'b010;  //+2
      	3'b100:    dout = 3'b110;  //-2
      	3'b101:    dout = 3'b111;  //-1
      	3'b110:    dout = 3'b111;  //-1
		Default :   dout = 3'b000;  //-0
    end
end

对于基系数的取值范围：-2~2，它们对部分积的影响有以下几个方面：
1、-2、2，被乘数需要乘以2
2、-2、-1 被乘数取反
3、0，部分积为0
为降低电路面积、功耗，直接将dout的3bit数重新赋值

input 	[2:0] 		din;
input 	[DW-1:0] 	a;
output        		e;
output        		s;
output 	[DW:0]  	part_mul;

//Wire [2:0]  din;
wire [2:0]  	dout;
wire        	two;
wire        	zero;
wire        	neg;
wire [DW-1:0]  	a_tmp;
//Wire [DW:0]  part_mul;

always @ （*）    begin
    case(din)    begin
      	3'b000:    dout = 3'b010;  //+0
      	3'b001:    dout = 3'b000;  //+1
      	3'b010:    dout = 3'b000;  //+1
      	3'b011:    dout = 3'b100;  //+2
      	3'b100:    dout = 3'b101;  //-2
      	3'b101:    dout = 3'b001;  //-1
      	3'b110:    dout = 3'b001;  //-1
		default :   dout = 3'b011;  //-0
    end
end
assign two = dout[2];
assign zero = dout[1];
assign neg = dout[0];

assign a_tmp = {DW{zero}} & a;
assign part_mul = {{DW}neg} ^ {two ? {a_tmp,1'b0} : {a_tmp[DW-1],a_tmp}};
assign e = a[DW-1] ^ neg;
assign s = neg;