【力扣刷题笔记】中级算法
中级算法(7.22-8.21)
数组和字符串
三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
示例 2:
输入:nums = []
输出:[]
示例 3:
输入:nums = [0]
输出:[]
提示:
0 <= nums.length <= 3000
-105 <= nums[i] <= 105
链接:https://leetcode.cn/leetbook/read/top-interview-questions-medium/xvpj16/
我的解法
企图用哈希解法未遂
去重的过程不好处理,有很多小细节
标答
思路:排序+双指针
class Solution {
public:
vector> threeSum(vector& nums)
{
int size = nums.size();
if (size < 3) return {}; // 特判
vector >res; // 保存结果(所有不重复的三元组)
std::sort(nums.begin(), nums.end());// 排序(默认递增)
for (int i = 0; i < size; i++) // 固定第一个数,转化为求两数之和
{
if (nums[i] > 0) return res; // 第一个数大于 0,后面都是递增正数,不可能相加为零了
// 去重:如果此数已经选取过,跳过
if (i > 0 && nums[i] == nums[i-1]) continue;
// 双指针在nums[i]后面的区间中寻找和为0-nums[i]的另外两个数
int left = i + 1;
int right = size - 1;
while (left < right)
{
if (nums[left] + nums[right] > -nums[i])
right--; // 两数之和太大,右指针左移
else if (nums[left] + nums[right] < -nums[i])
left++; // 两数之和太小,左指针右移
else
{
// 找到一个和为零的三元组,添加到结果中,左右指针内缩,继续寻找
res.push_back(vector{nums[i], nums[left], nums[right]});
left++;
right--;
// 去重:第二个数和第三个数也不重复选取
// 例如:[-4,1,1,1,2,3,3,3], i=0, left=1, right=5
while (left < right && nums[left] == nums[left-1]) left++;
while (left < right && nums[right] == nums[right+1]) right--;
}
}
}
return res;
}
};
根据标答自己写的代码
class Solution {
public:
vector> threeSum(vector& nums) {
vector> ans;
sort(nums.begin(),nums.end());
int n=nums.size();
for(int i=0;i=1&&nums[i]==nums[i-1])
{
continue;
}
int target=-nums[i];
int l=i+1,r=n-1;
while(ltarget)
{
while(r>0&&nums[r]==nums[r-1])
r--;
r--;
}
else
{
vector row;
row.push_back(nums[i]);
row.push_back(nums[l]);
row.push_back(nums[r]);
ans.push_back(row);
while(l0&&nums[r]==nums[r-1])
r--;
r--;
}
}
}
return ans;
}
};
疑惑解答
1.为什么双指针的单向运行不会使正确答案跳过?
思路:证明每一个正确答案都会被发现
2.为什么第一层循环可以跳过重复的元素而不会导致漏解
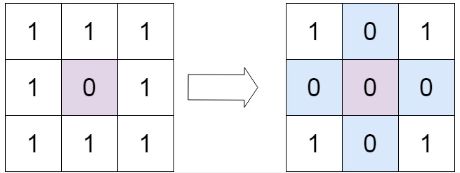
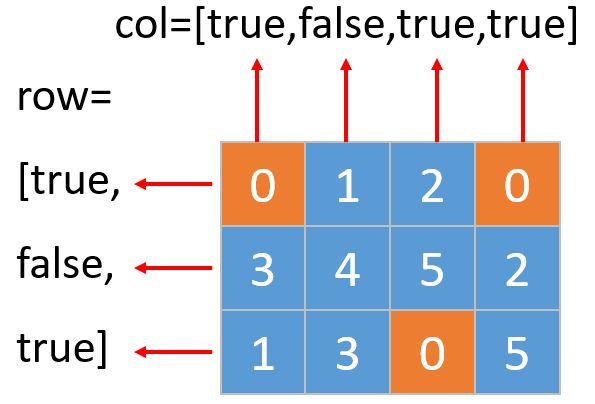
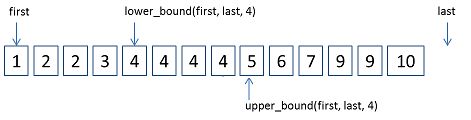
由于i 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例 1: 示例 2: 提示: 进阶: 一个直观的解决方案是使用 O(mn) 的额外空间,但这并不是一个好的解决方案。 没有想到比O(m+n)更好的算法了 一、使用两个标记变量 我们可以用矩阵的第一行和第一列代替方法一中的两个标记数组,以达到 O(1)的额外空间。但这样会导致原数组的第一行和第一列被修改,无法记录它们是否原本包含 0。因此我们需要额外使用两个标记变量分别记录第一行和第一列是否原本包含 0。 二、使用一个变量标记 我们可以对方法二进一步优化,只使用一个标记变量记录第一列是否原本存在 0。这样,第一列的第一个元素即可以标记第一行是否出现 0。 但为了防止每一列的第一个元素被提前更新,我们需要从最后一行开始,倒序地处理矩阵元素。 官解虽短但不好理解,自己写了一个 1、当利用常数空间时,想想是不是可以把结构塞到原有结构中 2、正确性证明: 关键:覆盖了的本来也需要改,没覆盖的正好不需要改 [1…n] [1…n]:算法正确性同利用O(m+n)空间算法,唯一要说明的是若本来第一行、第一列为0,则[1…n] [1…n]也要修改(有点外力指定那种意思) 第一行(列):若被上一过程[1…n] [1…n]修改成0了,说明它本来也要被改成0,修改正确!若没有被修改则说明当前列(行)没有0,唯一被修改的可能就是因为第一行内部本来就有的0;若row0标记true,则修改为0,正确!若row0标记false,则不修改,正确! 给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。 字母异位词 是由重新排列源单词的字母得到的一个新单词,所有源单词中的字母通常恰好只用一次。 示例 1: 示例 2: 示例 3: 提示: 两个字符串互为字母异位词,当且仅当两个字符串包含的字母相同。同一组字母异位词中的字符串具备相同点,可以使用相同点作为一组字母异位词的标志,使用哈希表存储每一组字母异位词,哈希表的键为一组字母异位词的标志,哈希表的值为一组字母异位词列表。 遍历每个字符串,对于每个字符串,得到该字符串所在的一组字母异位词的标志,将当前字符串加入该组字母异位词的列表中。遍历全部字符串之后,哈希表中的每个键值对即为一组字母异位词。 以下的两种方法分别使用排序和计数作为哈希表的键。 遇到这种有共同特征的一组数/字符串想想哈希! 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 示例 2: 示例 3: 提示: 链接:https://leetcode.cn/leetbook/read/top-interview-questions-medium/xv2kgi/ 双指针(滑动窗口) DP 给你一个字符串 s,找到 s 中最长的回文子串。 示例 1: 示例 2: 提示: DP(一开始用的一维DP,差点没写出来) https://www.jianshu.com/p/392172762e55 时间复杂度:for 循环里边套了一层 while 循环,难道不是 O ( n² )?不!其实是 O ( n )。不严谨的想一下,因为 while 循环访问 R 右边的数字用来扩展,也就是那些还未求出的节点,然后不断扩展,而期间访问的节点下次就不会再进入 while 了,可以利用对称得到自己的解,所以每个节点访问都是常数次,所以是O ( n )。 给你一个整数数组 nums ,判断这个数组中是否存在长度为 3 的递增子序列。 如果存在这样的三元组下标 (i, j, k) 且满足 i < j < k ,使得 nums[i] < nums[j] < nums[k] ,返回 true ;否则,返回 false 。 示例 1: 示例 2: 示例 3: 提示: 进阶:你能实现时间复杂度为 O(n) ,空间复杂度为 O(1) 的解决方案吗? 链接:https://leetcode.cn/leetbook/read/top-interview-questions-medium/xvvuqg/ 一、双向遍历 二、一次遍历贪心 给你一个整数数组 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如, 示例 1: 示例 2: 示例 3: 提示: 参照:https://leetcode.cn/problems/longest-increasing-subsequence/solution/yi-bu-yi-bu-tui-dao-chu-guan-fang-zui-you-jie-fa-x/ 关键就在于这张图:表示所有可能在将来成为最长递增子序列的序列 与DP的感觉差不多,表示【0-i】里长度为k上升序列尾端的最小值 讲的很好! lower/upper_bound()的底层也是二分查找 给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。 题目数据 保证 整个链式结构中不存在环。 注意,函数返回结果后,链表必须 保持其原始结构 。 链接:https://leetcode.cn/leetbook/read/top-interview-questions-medium/xv02ut/ 进阶:你能否设计一个时间复杂度 空间O(m+n) 如果两个链表相交,那么相交点之后的长度是相同的 我们需要做的事情是,让两个链表从同距离末尾同等距离的位置开始遍历。这个位置只能是较短链表的头结点位置。 指针 pA 指向 A 链表,指针 pB 指向 B 链表,依次往后遍历 给定一个仅包含数字 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。 示例 1: 示例 2: 示例 3: 提示: 回溯:实际遍历过程相当于DFS! 队列:实际遍历过程相当于BFS! 回溯模版 难度中等2789 数字 示例 1: 示例 2: 提示: 差不多但是代码更加优美 难度中等1391 给定一个 单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。 示例 1: 示例 2: 示例 3: 提示: **进阶:**你可以使用搜索剪枝的技术来优化解决方案,使其在 思路一致但代码更为优美 难度中等1274 给你一个整数数组 示例 1: 示例 2: 提示: **进阶:**你所设计算法的时间复杂度 必须 优于 不好,没必要全部都排序出来 一、堆 二、快排 给定整数数组 请注意,你需要找的是数组排序后的第 示例 1: 示例 2: 提示: 一、partition 二、堆 建堆、删除 以数组 示例 1: 示例 2: 提示: 维护前面区间中最右边的端点为ed。从前往后枚举每一个区间,判断是否应该将当前区间视为新区间。 引理:如果我们按照区间的左端点排序,那么在排完序的列表中,可以合并的区间一定是连续的。 证明:两个可以合并的区间中间没有不可以和他们俩合并的区间(有点并查集的感觉、染色) 上述算法的正确性可以用反证法来证明:在排完序后的数组中,两个本应合并的区间没能被合并,那么说明存在这样的三元组 (i, j, k)以及数组中的三个区间 a[i], a[j], a[k]满足 i < j < k 并且 (a[i], a[k])可以合并,但 (a[i],a[j]) 和 (a[j],a[k]) 不能合并。这说明它们满足下面的不等式: $a[i].end < a[j].start \quad (a[i] \text{ 和 } a[j] \text{ 不能合并}) \ a[j].end < a[k].start \quad (a[j] \text{ 和 } a[k] \text{ 不能合并}) \ a[i].end \geq a[k].start \quad (a[i] \text{ 和 } a[k] \text{ 可以合并}) \$ 我们联立这些不等式(注意还有一个显然的不等式 a [ j ] . s t a r t ≤ a [ j ] . e n d a[j].start \leq a[j].end a[j].start≤a[j].end),可以得到: [ i ] . e n d < a [ j ] . s t a r t ≤ a [ j ] . e n d < a [ k ] . s t a r t [i].end < a[j].start \leq a[j].end < a[k].start [i].end<a[j].start≤a[j].end<a[k].start 产生了矛盾!这说明假设是不成立的。因此,所有能够合并的区间都必然是连续的。 难度中等1942 给定一个非负整数数组 数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标。 示例 1: 示例 2: 提示: 有点被大标题误导了只往DP上想(说明当代年轻人真容易被带节奏) 还是要坚持自己的思考啊 实现 pow(x, n) ,即计算 示例 1: 示例 2: 示例 3: 提示: 快速幂乘法O(logn):解说 难度中等961 给定两个整数,被除数 返回被除数 整数除法的结果应当截去( 示例 1: 示例 2: 提示: 被除数和除数均为 32 位有符号整数。 除数不为 0。 假设我们的环境只能存储 32 位有符号整数,其数值范围是 [−231, 231 − 1]。本题中,如果除法结果溢出,则返回 231 − 1。 关键:类二分查找 难度中等406 给定两个整数,分别表示分数的分子 如果小数部分为循环小数,则将循环的部分括在括号内。 如果存在多个答案,只需返回 任意一个 。 对于所有给定的输入,保证 答案字符串的长度小于 示例 1: 示例 2: 示例 3: 提示: 难度中等989 给你一个用字符数组 然而,两个 相同种类 的任务之间必须有长度为整数 你需要计算完成所有任务所需要的 最短时间 。 示例 1: 示例 2: 示例 3: 提示: https://leetcode.cn/problems/task-scheduler/solution/tong-zi-by-popopop/ 做中级的时间明显比初级的时间长了不少 一方面是题目确实更有有难度和思维性,另一方面是这几天出去旅游各种玩没沉下心来 继续努力矩阵置零
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-2^31 <= matrix[i][j] <= 2^31 - 1
一个简单的改进方案是使用 O(m + n) 的额外空间,但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗?
链接:https://leetcode.cn/leetbook/read/top-interview-questions-medium/xvmy42/我的解法
class Solution {
public:
void setZeroes(vector官解
class Solution {
public:
void setZeroes(vectorclass Solution {
public:
void setZeroes(vector总结思考
字母异位词分组
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
输入: strs = [""]
输出: [[""]]
输入: strs = ["a"]
输出: [["a"]]
我的解法
class Solution {
public:
vector官解
class Solution {
public:
vector class Solution {
public:
vector反思
无重复字符的最长子串
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
0 <= s.length <= 5 * 10^4
s 由英文字母、数字、符号和空格组成
我的解法
class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_mapclass Solution {
public:
int lengthOfLongestSubstring(string s) {
int n=s.length();
if(n==0)
{
return 0;
}
int* last=new int[n];
unordered_map最长回文子串
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
输入:s = "cbbd"
输出:"bb"
1 <= s.length <= 1000
s 仅由数字和英文字母组成
我的解法
class Solution {
public:
string longestPalindrome(string s) {
int n=s.size();
string ans;int l=0,r=0,max=1;
vectorManacher 算法
class Solution {
public:
string longestPalindrome(string s) {
int n=s.size();
string t="";
for(int i=0;i递增的三元子序列
输入:nums = [1,2,3,4,5]
输出:true
解释:任何 i < j < k 的三元组都满足题意
输入:nums = [5,4,3,2,1]
输出:false
解释:不存在满足题意的三元组
输入:nums = [2,1,5,0,4,6]
输出:true
解释:三元组 (3, 4, 5) 满足题意,因为 nums[3] == 0 < nums[4] == 4 < nums[5] == 6
1 <= nums.length <= 5 * 10^5
-2^31 <= nums[i] <= 2^31 - 1
解法
class Solution {
public:
bool increasingTriplet(vectorclass Solution {
public:
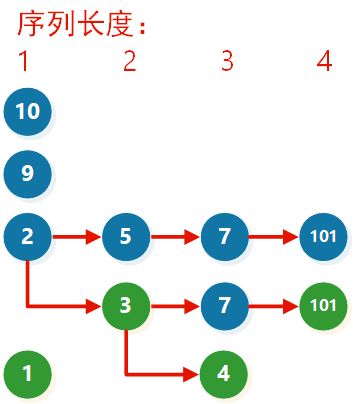
bool increasingTriplet(vector*300. 最长递增子序列
nums ,找到其中最长严格递增子序列的长度。[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
输入:nums = [0,1,0,3,2,3]
输出:4
输入:nums = [7,7,7,7,7,7,7]
输出:1
1 <= nums.length <= 2500-104 <= nums[i] <= 104题解
class Solution {
public:
int lengthOfLIS(vector链表
*相交链表
O(m + n) 、仅用 O(1) 内存的解决方案?我的解法
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
unordered_map官解
如果 pA 到了末尾,则 pA = headB 继续遍历
如果 pB 到了末尾,则 pB = headA 继续遍历回溯算法
17. 电话号码的字母组合
2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
输入:digits = ""
输出:[]
输入:digits = "2"
输出:["a","b","c"]
0 <= digits.length <= 4digits[i] 是范围 ['2', '9'] 的一个数字。我的解法
class Solution {
public:
vector另外一种解法
class Solution {
public List<String> letterCombinations(String digits) {
if(digits==null || digits.length()==0) {
return new ArrayList<String>();
}
//一个映射表,第二个位置是"abc“,第三个位置是"def"。。。
//这里也可以用map,用数组可以更节省点内存
String[] letter_map = {
" ","*","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"
};
List<String> res = new ArrayList<>();
//先往队列中加入一个空字符
res.add("");
for(int i=0;i<digits.length();i++) {
//由当前遍历到的字符,取字典表中查找对应的字符串
String letters = letter_map[digits.charAt(i)-'0'];
int size = res.size();
//计算出队列长度后,将队列中的每个元素挨个拿出来
for(int j=0;j<size;j++) {
//每次都从队列中拿出第一个元素
String tmp = res.remove(0);
//然后跟"def"这样的字符串拼接,并再次放到队列中
for(int k=0;k<letters.length();k++) {
res.add(tmp+letters.charAt(k));
}
}
}
return res;
}
}
总结
void backtrack(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtrack(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
22. 括号生成
n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
输入:n = 1
输出:["()"]
1 <= n <= 8我的解法
class Solution {
public:
vector官解
class Solution {
void backtrack(vector79. 单词搜索
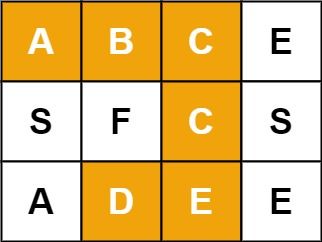
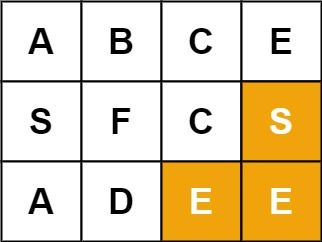
m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出:true
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出:false
m == board.lengthn = board[i].length1 <= m, n <= 61 <= word.length <= 15board 和 word 仅由大小写英文字母组成board 更大的情况下可以更快解决问题?我的解法
class Solution {
public:
string cur;
int m,n,len;
bool ans;
bool exist(vector官解
class Solution {
public:
bool check(vector排序与搜索
347. 前 K 个高频元素
nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
输入: nums = [1], k = 1
输出: [1]
1 <= nums.length <= 105k 的取值范围是 [1, 数组中不相同的元素的个数]k 个高频元素的集合是唯一的O(n log n) ,其中 n 是数组大小。我的解法
class Solution {
public:
vector官解
class Solution {
public:
static bool cmp(pairclass Solution {
public:
void qsort(vector215. 数组中的第K个最大元素
nums 和整数 k,请返回数组中第 **k** 个最大的元素。k 个最大的元素,而不是第 k 个不同的元素。输入: [3,2,1,5,6,4], k = 2
输出: 5
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
1 <= k <= nums.length <= 105-104 <= nums[i] <= 104解法
class Solution {
public:
int findKthLargest(vectorclass Solution {
public:
void maxHeapify(vector*56. 合并区间
intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104解法
class Solution {
public:
vector动态规划
55. 跳跃游戏
nums ,你最初位于数组的 第一个下标 。输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
1 <= nums.length <= 3 * 1040 <= nums[i] <= 105我的解法
class Solution {
public:
bool canJump(vector官解
class Solution {
public:
bool canJump(vector数学
50. Pow(x, n)
x 的整数 n 次幂函数(即,xn )。输入:x = 2.00000, n = 10
输出:1024.00000
输入:x = 2.10000, n = 3
输出:9.26100
输入:x = 2.00000, n = -2
输出:0.25000
解释:2-2 = 1/22 = 1/4 = 0.25
-100.0 < x < 100.0-231 <= n <= 231-1-104 <= xn <= 104解法
class Solution {
public:
double myPow(double x, int n) {
if(n==0) return 1;
long long N=n;
int sign;
if(n<0)
{
N=-N;
sign=-1;
}
else
{
sign=1;
}
double contribute=x;
double ans=1;
while(N!=0)
{
if(N%2) ans*=contribute;
contribute*=contribute;
N>>=1;
}
return sign==1?ans:1.0/ans;
}
};
29. 两数相除
dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。dividend 除以除数 divisor 得到的商。truncate)其小数部分,例如:truncate(8.345) = 8 以及 truncate(-2.7335) = -2输入: dividend = 10, divisor = 3
输出: 3
解释: 10/3 = truncate(3.33333..) = truncate(3) = 3
输入: dividend = 7, divisor = -3
输出: -2
解释: 7/-3 = truncate(-2.33333..) = -2
解法
class Solution {
public:
int divide(int dividend, int divisor) {
if(dividend==-2147483648)
{
if(divisor==-1)
return 2147483647;
if(divisor==1)
return -2147483648;
}
if(divisor==-2147483648)
{
return dividend==-2147483648?1:0;
}
bool rev = false;
if (dividend > 0) {
dividend = -dividend;
rev = !rev;
}
if (divisor > 0) {
divisor = -divisor;
rev = !rev;
}
//写法一:预先计算好
vector166. 分数到小数
numerator 和分母 denominator,以 字符串形式返回小数 。104 。输入:numerator = 1, denominator = 2
输出:"0.5"
输入:numerator = 2, denominator = 1
输出:"2"
输入:numerator = 4, denominator = 333
输出:"0.(012)"
-231 <= numerator, denominator <= 231 - 1denominator != 0解法
class Solution {
public:
string fractionToDecimal(int numerator, int denominator) {
long numeratorLong = numerator;
long denominatorLong = denominator;
if (numeratorLong % denominatorLong == 0) {
return to_string(numeratorLong / denominatorLong);
}
string ans;
if (numeratorLong < 0 ^ denominatorLong < 0) {
ans.push_back('-');
}
// 整数部分
numeratorLong = abs(numeratorLong);
denominatorLong = abs(denominatorLong);
long integerPart = numeratorLong / denominatorLong;
ans += to_string(integerPart);
ans.push_back('.');
// 小数部分
string fractionPart;
unordered_map其他
621. 任务调度器
tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行,并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间,CPU 可以完成一个任务,或者处于待命状态。n 的冷却时间,因此至少有连续 n 个单位时间内 CPU 在执行不同的任务,或者在待命状态。输入:tasks = ["A","A","A","B","B","B"], n = 2
输出:8
解释:A -> B -> (待命) -> A -> B -> (待命) -> A -> B
在本示例中,两个相同类型任务之间必须间隔长度为 n = 2 的冷却时间,而执行一个任务只需要一个单位时间,所以中间出现了(待命)状态。
输入:tasks = ["A","A","A","B","B","B"], n = 0
输出:6
解释:在这种情况下,任何大小为 6 的排列都可以满足要求,因为 n = 0
["A","A","A","B","B","B"]
["A","B","A","B","A","B"]
["B","B","B","A","A","A"]
...
诸如此类
输入:tasks = ["A","A","A","A","A","A","B","C","D","E","F","G"], n = 2
输出:16
解释:一种可能的解决方案是:
A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> (待命) -> (待命) -> A -> (待命) -> (待命) -> A
1 <= task.length <= 104tasks[i] 是大写英文字母n 的取值范围为 [0, 100]解法
int leastInterval(vector总结