融合Sin混沌和分段权值的阿基米德优化算法-附代码
融合Sin混沌和分段权值的阿基米德优化算法
文章目录
- 融合Sin混沌和分段权值的阿基米德优化算法
-
- 1.阿基米德优化算法
- 2. 改进阿基米德优化算法
-
- 2.1 Sin混沌反向学习初始化策略
- 2.2 算数交叉算子
- 2.3 分段权值策略
- 3.实验结果
- 4.参考文献
- 5.Matlab代码
- 6.Python代码
摘要:针对阿基米德优化算法(Archimedes Optimization Algorithm,AOA)存在全局搜索能力弱、收敛精度低,易陷入局部最优等问题,提出融合Sin混沌和分段权值的阿基米德优化算法(SAOA)。首先,采用无限折叠迭代的Sin混沌反向学习策略初始化种群,提高初始阶段解的质量,为全局搜索多样性奠定基础;其次,引入算数交叉算子,将当前个体向与全局最优个体进行交叉,引导种群向最优解区域寻优,提高全局搜索能力;同时,引入分段权值策略,平衡算法的全局勘探与局部开发能力,降低算法陷入局部最优的概率;
1.阿基米德优化算法
基础阿基米德优化算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/119999874
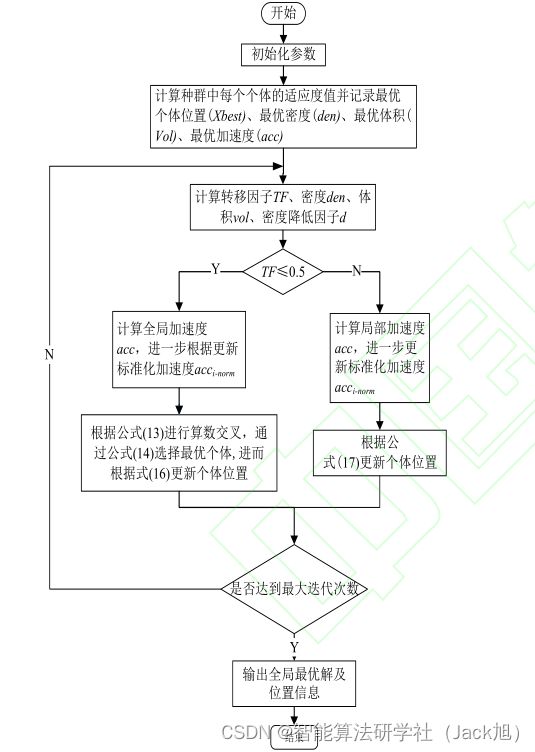
2. 改进阿基米德优化算法
2.1 Sin混沌反向学习初始化策略
种群初始多样性可以有效地扩大算法的搜索范围, 从而提高算法的寻优精度和收敛速度 [ 11 ] { }^{[11]} [11] 。混沌经常被 用于优化问题, 其基本原理是通过映射关系在混沌变 量空间 [ 0 , 1 ] [0,1] [0,1] 之间产生混沌序列, 再将其转化到个体的 优化变量空间内。 Sin \operatorname{Sin} Sin 混沌模型是一种具有较好遍历 性和随机性的映射折叠次数无限的混沌模型。反向学 好的解, 从而引导个体寻找最优解。因此, 本文先利 用 Sin 混沌产生多样性较好的初始种群; 其次, 根据 反向学习产生反向种群; 最后, 分别计算 Sin 混沌初 始种群及反向种群的适应度, 选择适应度低的解作为 初始种群, 提高了找到最优初始解的概率, 从而使种 群向全局最优解靠近。Sin 混沌 1 维映射表达式如下:
{ X n + 1 = sin ( 2 / X n ) n = 0 , 1 , … , N − 1 ≤ X n ≤ 1 X n ≠ 0 (10) \begin{cases}X_{n+1}=\sin \left(2 / X_n\right) & n=0,1, \ldots, N \\ -1 \leq X_n \leq 1 & X_n \neq 0\end{cases} \tag{10} {Xn+1=sin(2/Xn)−1≤Xn≤1n=0,1,…,NXn=0(10)
式 (10): X n X_{\mathrm{n}} Xn 是取值为 ( − 1 , 1 ) (-1,1) (−1,1) 的序列且初始值不能设置为 0 。将 Sin 混沌序列映射到解空间中, 得到种群 X = { X i X=\left\{X_i\right. X={Xi, i = 1 , 2 , … N } , X j = { X j , j = 1 , 2 , … , dim } i=1,2, \ldots N\}, X_j=\left\{X_j, j=1,2, \ldots, \operatorname{dim}\right\} i=1,2,…N},Xj={Xj,j=1,2,…,dim}, 种群个体表示如 F:
X i + 1 , j = sin ( 2 / X i , j ) (11) X_{i+1, j}=\sin \left(2 / X_{i, j}\right) \tag{11} Xi+1,j=sin(2/Xi,j)(11)
式中: X i + 1 , j X_{i+1, j} Xi+1,j 为第 i + 1 i+1 i+1 个种群的第 j j j 维值。
由种群 X X X 计算反向种群 X ∗ = { X i ∗ , i = 1 , 2 , … , N } X^*=\left\{X_i^*, i=1,2, \ldots, N\right\} X∗={Xi∗,i=1,2,…,N},
X i ∗ = { X i j ∗ , j = 1 , 2 , … , dim } X_i^*=\left\{X_{i j}^*, j=1,2, \ldots, \operatorname{dim}\right\} Xi∗={Xij∗,j=1,2,…,dim}, 反向种群个体 X i j ∗ X_{i j}{ }^* Xij∗ 表示如下:
X i j ∗ = x min j + x max j − X i j (12) X_{i j}^*=x_{\min j}+x_{\max j}-X_{i j} \tag{12} Xij∗=xminj+xmaxj−Xij(12)
式中: [ X minj , X maxj ] \left[X_{\operatorname{minj}}, X_{\operatorname{maxj}}\right] [Xminj,Xmaxj] 为搜索空间的动态边界。将 Sin \operatorname{Sin} Sin 混 池种群 X X X 和反向种群 X ∗ X^* X∗ 组成新种群 { X ∪ X ∗ } \left\{X \cup X^*\right\} {X∪X∗}, 将新种 群的适应度值进行排序, 选择 N N N 个适应度值最优的个 体组成初始种群。
2.2 算数交叉算子
在标准的 AOA 中,碰撞个体根据公式(6)迚行全局搜索,由于没有任何先验条件可以使用,仅依靠种群中随机个体的引导迚行种群位置更新,随机个体可能是一个质量较好的解,也可能是一个较差的解,导致算法的全局寻优性能较弱。因此,为提高标准AOA 的全局搜索性能,本文引入的算术交叉算子,表达式如公式(13)所示:
X n e w t + 1 = λ × X i t + 1 + ( 1 − λ ) × ( X best − X i t + 1 ) (13) X_{n e w}^{t+1}=\lambda \times X_i^{t+1}+(1-\lambda) \times\left(X_{\text {best }}-X_i^{t+1}\right) \tag{13} Xnewt+1=λ×Xit+1+(1−λ)×(Xbest −Xit+1)(13)
式中: λ ∈ ( 0 , 1 ) \lambda \in(0,1) λ∈(0,1) 表示随机数。
SAOA 选择当前个体与全局最优个体进行算术交 叉, 产生新的子代个体更靠近当前最优解, 从而加快 群体向全局最优区域靠笼, 同时算术交叉算子给予当 前个体向优秀个体学习的能力, 增强种群信息分享能 力, 从而增加种群多样性。将当前个体与全局最优个 体进行交叉后, 虽然能增强算法全局搜索能力, 但是 无法直接判断产生的新个体是否优于原始个体。因此, 通过交叉选择后, 利用贪婪机制比较新旧个体适应度 值, 再决定是否更新当前个体, 通过这种方式不断获 得更优解, 从而提升算法全局寻优性能。其中贪婪机 制的数学模型如公式(14)所示:
X i t + 1 = { X i t + 1 f ( X i t + 1 ) < f ( X new t + 1 ) X new t + 1 f ( X i t + 1 ) ≥ f ( X new t + 1 ) (14) X_i^{t+1}= \begin{cases}X_i^{t+1} & f\left(X_i^{t+1}\right)
2.3 分段权值策略
在标准 A O A \mathrm{AOA} AOA 中, 转移因子 T F T F TF 取值为 ( 0.36 , 1 ) (0.36,1) (0.36,1), 当 T F > 0.5 T F>0.5 TF>0.5 时, 算法进行局部开发, 最优个体引导种 群进行位置更新, 但是当最优个体陷人局部极值空间 时, 种群将受其影响陷人局部最优, 使得算法出现 “早熟”现象。为解决这个问题,本文提出分段权值 的位置更新策略, 首先, 借鉴双曲正切函数的思想, 本文在算法迭代前中期种群位置更新处引人动态双曲 正切权值 w w w, 其值随迭代次数的增加呈非线性递减, 其次, 在算法迭代后期, 引人正弦波动权值, 降低算 法陷人局部最优的概率。本文所采用的动态双曲正切 权值, 在算法迭代前期, S A O A \mathrm{SAOA} SAOA 获得较大权值以保证 其在更广阔的区域搜索最优解, 在算法迭代中期, SAOA 获得较小权值, 使当前个体可以在最优个体附 进行精确搜索,达到平衡全局搜索与局部开发的能力, 算法迭代后期, 利用正弦波不规则变换的特点来增强 最优个体在局部空间开发的多元性, 协助种群跳出局 部最优。分段权值 w w w 的计算公式如(15)所示:
{ w = w start − ( w start − w end ) × tanh ( ( α × p i × ( t / t max ) ) ) t ≤ δ w = β 1 × ( ( β 2 × p i × t + β 3 × p i ) + θ ) t > δ (15) \begin{cases}w=w_{\text {start }}-\left(w_{\text {start }}-w_{\text {end }}\right) \times \tanh \left(\left(\alpha \times p i \times\left(t / t_{\max }\right)\right)\right) & t \leq \delta \\ w=\beta_1 \times\left(\left(\beta_2 \times p i \times t+\beta_3 \times p i\right)+\theta\right) & t>\delta\end{cases} \tag{15} {w=wstart −(wstart −wend )×tanh((α×pi×(t/tmax)))w=β1×((β2×pi×t+β3×pi)+θ)t≤δt>δ(15)
式中: w start w_{\text {start }} wstart 表示迭代开始时的初始权值, 即当 t = 0 t=0 t=0 时, w start = 0.8 , w end w_{\text {start }}=0.8, w_{\text {end }} wstart =0.8,wend 表示迭代结束时的权值, 即当 t = t max t=t_{\text {max }} t=tmax , w end = 0.4 ∘ δ w_{\text {end }}=0.4 \circ \delta wend =0.4∘δ 为迭代次数, β 1 = 0.23 , β 3 = 1.6 , θ = 0.3 。 α \beta_1=0.23 , \beta_3=1.6 , \theta=0.3 。 \alpha β1=0.23,β3=1.6,θ=0.3。α和 β 2 \beta_2 β2 为调节因子, 控制曲线的平滑度, 经过多次实验 验证, 当 α = 0.75 \alpha=0.75 α=0.75 和 β 2 = 0.06 \beta_2=0.06 β2=0.06 时, 实验结果为最优。
因此,AOA 引入分段权值策略后全局搜索阶段的个体位置更新公式为:
x i t + 1 = w × x i t + c 1 × r a n d × a c c i − norm t + 1 × d × ( x rand − x i t ) (16) x_i^{t+1}=w \times x_i^t+c_1 \times rand \times a c c_{i-\text { norm }}^{t+1} \times d \times\left(x_{\text {rand }}-x_i^t\right)\tag{16} xit+1=w×xit+c1×rand×acci− norm t+1×d×(xrand −xit)(16)
局部开发阶段个体位置更新公式为:
x i t + 1 = w × x bet t + F × c 2 × rand × a c c i − nomn t + 1 × d × ( T × x bet − x i t ) (17) x_i^{t+1}=w \times x_{\text {bet }}^t+F \times c_2 \times \text { rand } \times a c c_{i-\text { nomn }}^{t+1} \times d \times\left(T \times x_{\text {bet }}-x_i^t\right)\tag{17} xit+1=w×xbet t+F×c2× rand ×acci− nomn t+1×d×(T×xbet −xit)(17)
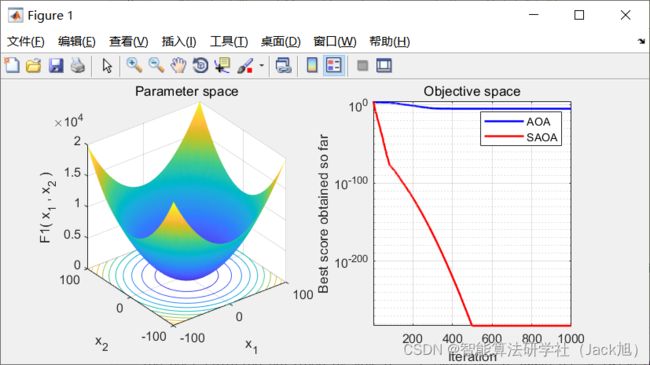
3.实验结果
4.参考文献
[1]罗仕杭,何庆.融合Sin混沌和分段权值的阿基米德优化算法[J/OL].计算机工程与应用:1-12[2021-10-12].http://kns.cnki.net/kcms/detail/11.2127.TP.20210913.1319.012.html.