【算法分析与设计】回溯法（下）

---

一、符号三角形问题

  下图是由14个“+”和14个“-”组成的符号三角形。2个同号下面都是“+”，2个异号下面都是“-”。

  在一般情况下，符号三角形的第一行有n个符号。符号三角形问题要求对于给定的n，计算有多少个不同的符号三角形，使其所含的“+”和“-”的个数相同。
  解向量：用n元组x[1:n]表示符号三角形的第一行。
  可行性约束函数：当前符号三角形所包含的“+”个数与“-”个数均不超过n*(n+1)/4
  无解的判断：n * (n+1)/2为奇数。

void Triangle::Backtrack(int t)
{
  if ((count>half)||(t*(t-1)/2-count>half)) return;
  if (t>n) sum++;
    else
      for (int i=0;i<2;i++) {
        p[1][t]=i;
        count+=i;
        for (int j=2;j<=t;j++) {
          p[j][t-j+1]=p[j-1][t-j+1]^p[j-1][t-j+2];
          count+=p[j][t-j+1];
        }
      Backtrack(t+1);
      for (int j=2;j<=t;j++)
        count-=p[j][t-j+1];
      count-=i;
     }
  }

  复杂度分析：
  计算可行性约束需要O(n)时间，在最坏情况下有 O(2n)个结点需要计算可行性约束，故解符号三角形问题的回溯算法所需的计算时间为 O(n2n)。

---

二、N皇后问题

  在n×n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n后问题等价于在n×n格的棋盘上放置n个皇后，任何2个皇后不放在同一行或同一列或同一斜线上。

  解向量：(x1, x2, … , xn)
  显约束：xi=1,2, … ,n
  隐约束：
  1)不同列：xixj
  2)不处于同一正、反对角线：|i-j||xi-xj|

bool Queen::Place(int k)
{
  for (int j=1;j<k;j++)
    if ((abs(k-j)==abs(x[j]-x[k]))||(x[j]==x[k])) return false;
  return true;
} 

void Queen::Backtrack(int t)
{
  if (t>n) sum++;
    else
      for (int i=1;i<=n;i++) {
        x[t]=i;
        if (Place(t)) Backtrack(t+1);
      }
 }

---

三、0-1背包问题

  左子树可行进入，否则不进。
  右子树可能包含最优解才进，否则不进。
  cp（当前价值）+r（剩余物品价值和）<=bestp（当前最优价值）。
  可以先排序，再计算得出非整数解，作为最优解的“天花板”
  将物品按照单位重量价值从大到小排序，然后按顺序考察各物品。

  解空间：子集树：
  可行性约束函数：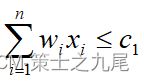
  上界函数：cp（当前价值）+r（剩余物品价值和）<=bestp（当前最优价值）。

template<class Typew, class Typep>
Typep Knap<Typew, Typep>::Bound(int i)
{// 计算上界
   Typew cleft = c - cw;  // 剩余容量
   Typep b = cp;
   // 以物品单位重量价值递减序装入物品
   while (i <= n && w[i] <= cleft) {
      cleft -= w[i];
      b += p[i];
      i++;
      }
   // 装满背包
   if (i <= n) b += p[i]/w[i] * cleft;
   return b;
}

  N=4 C=7
  P={9,10,7,4}
  W={3,5,2,1}
  最优解x={1,0,1,1}
  重量为6，价值为20
  复杂度分析：
  0-1背包问题的回溯算法所需的计算时间为O(n2n)。

---

四、最大团问题

  给定无向图G=(V，E)，求G的最大团。
  G的子图：G’=(V’，E’)，其中V’V，E’E
  G的补图：G=(V，E’)，E’是E关于完全图边集的补集
  G中的团：G的完全子图(任意)
  G的最大团：顶点数最多的团

  G的点独立集：G的顶点子集A，且任取两点u,v，其连线都不在E中。
  最大点独立集：顶点最多的点独立集。

  U是G的最大团当且仅当U是G的最大点独立集。


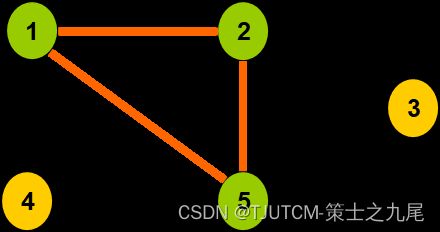
  解空间：子集树
  可行性约束函数：顶点i到已选入的顶点集中每一个顶点都有边相连。
  上界函数：有足够多的可选择顶点使得算法有可能在右子树中找到更大的团。

void Clique::Backtrack(int i)
{// 计算最大团
   if (i > n) {// 到达叶结点
      for (int j = 1; j <= n; j++) bestx[j] = x[j];
      bestn = cn;   return;}
   // 检查顶点 i 与当前团的连接
   int OK = 1;
   for (int j = 1; j < i; j++)
      if (x[j] && a[i][j] == 0) {
         // i与j不相连
         OK = 0;  break;}
   if (OK) {// 进入左子树
      x[i] = 1;  cn++;
      Backtrack(i+1);
      x[i] = 0; cn--;}
   if (cn + n - i > bestn) {// 进入右子树
      x[i] = 0;
      Backtrack(i+1);}
}

  复杂度分析：
  最大团问题的回溯算法backtrack所需的计算时间显然为O(n2n)。

---

4.1 进一步改进

  选择合适的搜索顺序，可以使得上界函数更有效的发挥作用。例如在搜索之前可以将顶点按度从小到大排序。这在某种意义上相当于给回溯法加入了启发性。
  定义Si={vi,vi+1,…,vn}，依次求出Sn,Sn-1,…,S1的解。从而得到一个更精确的上界函数，若cn+Si<=max则剪枝。同时注意到：从Si+1到Si，如果找到一个更大的团，那么vi必然属于找到的团，此时有Si=Si+1+1，否则Si=Si+1。因此只要max的值被更新过，就可以确定已经找到最大值，不必再往下搜索了。

---

五、图的m着色问题

  给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点着不同颜色。这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色，则称这个数m为该图的色数。求一个图的色数m的问题称为**图的m可着色优化问题**。

  由于用m种颜色为无向图G=(V, E)着色，其中，V的顶点个数为n，可以用一个n元组C=(c1, c2, …, cn)来描述图的一种可能着色，其中，ci∈{1, 2, …, m}(1≤i≤n)表示赋予顶点i的颜色。例如，5元组(1, 2, 2, 3, 1)表示对具有5个顶点的无向图的一种着色，顶点1着颜色1，顶点2着颜色2，顶点3着颜色2，如此等等。 如果在n元组C中，所有相邻顶点都不会着相同颜色，就称此n元组为可行解，否则为无效解。

---

5.1 算法设计

  搜索树：m叉树
  约束条件：在结点处，顶点c+1的邻接表中结点已用过的颜色不能再用
  如果邻接表中结点已用过m种颜色，则结点c+1没法着色，从该结点回溯到其父结点，满足多米诺性质。
  策略：深度优先。

  回溯法求解图着色问题，首先把所有顶点的颜色初始化为0，然后依次为每个顶点着色。在图着色问题的解空间树中，如果从根结点到当前结点对应一个部分解，也就是所有的颜色指派都没有冲突，则在当前结点处选择第一棵子树继续搜索，也就是为下一个顶点着颜色1，否则，对当前子树的兄弟子树继续搜索，也就是为当前顶点着下一个颜色，如果所有m种颜色都已尝试过并且都发生冲突，则回溯到当前结点的父结点处，上一个顶点的颜色被改变，依此类推。

  解向量：(x1, x2, … , xn)表示顶点i所着颜色x[i]
  可行性约束函数：顶点i与已着色的相邻顶点颜色不重复。

void Color::Backtrack(int t)
{
  if (t>n) {
   sum++;
   for (int i=1; i<=n; i++)
     cout << x[i] << ' ';
   cout << endl;
   }
    else
      for (int i=1;i<=m;i++) {
        x[t]=i;
        if (Ok(t)) Backtrack(t+1);
      }
}
bool Color::Ok(int k)
{// 检查颜色可用性
  for (int j=1;j<=n;j++)
    if ((a[k][j]==1)&&(x[j]==x[k])) return false;
  return true;
}

  复杂度分析
  图m可着色问题的解空间树中内结点个数是 。
  对于每一个内结点，在最坏情况下，用ok检查当前扩展结点的每一个儿子所相应的颜色可用性需耗时O(mn)。因此，回溯法总的时间耗费是

---

六、旅行售货员问题

  解空间：排列树。

template<class Type>
void Traveling<Type>::Backtrack(int i)
{
   if (i == n) {
      if (a[x[n-1]][x[n]] != NoEdge && a[x[n]][1] != NoEdge &&
         (cc + a[x[n-1]][x[n]] + a[x[n]][1] < bestc || bestc == NoEdge)) {
         for (int j = 1; j <= n; j++) bestx[j] = x[j];
         bestc = cc + a[x[n-1]][x[n]] + a[x[n]][1];}
      }
   else {
      for (int j = i; j <= n; j++)
         // 是否可进入x[j]子树?
         if (a[x[i-1]][x[j]] != NoEdge &&
            (cc + a[x[i-1]][x[i]] < bestc || bestc == NoEdge)) {
            // 搜索子树
            Swap(x[i], x[j]);
            cc += a[x[i-1]][x[i]];
            Backtrack(i+1);
            cc -= a[x[i-1]][x[i]];
            Swap(x[i], x[j]);}
      }
}

  复杂度分析：
  算法backtrack在最坏情况下可能需要更新当前最优解O((n-1)!)次，每次更新bestx需计算时间O(n)，从而整个算法的计算时间复杂性为O(n!)。

---

七、连续邮资问题

  假设国家发行了n种不同面值的邮票，并且规定每张信封上最多只允许贴m张邮票。连续邮资问题 要求对于给定的n和m的值，给出邮票面值的最佳设计，在1张信封上可贴出从邮资1开始，增量为1的最大连续邮资区间。
  例如，当n=5和m=4时，面值为(1,3,11,15,32)的5种邮票可以贴出邮资的最大连续邮资区间是1到70。
  面值为(1,6,10,20,30)的5种邮票只能贴出1-4,5无法贴出，不可取。
求给定n和m后，可以贴出连续邮资区间达到最大的最佳设计！

  解向量：用n元组x[1:n]表示n种不同的邮票面值，并约定它们从小到大排列。x[1]=1是唯一的选择。
  可行性约束函数：已选定x[1:i-1]，最大连续邮资区间是[1:r]，接下来x[i]的可取值范围是[x[i-1]+1:r+1]。
  如何确定r的值？
  计算X[1:i]的最大连续邮资区间在本算法中被频繁使用到，因此势必要找到一个高效的方法。考虑到直接递归的求解复杂度太高，我们不妨尝试计算用不超过m张面值为x[1:i]的邮票贴出邮资k所需的最少邮票数y[k]。通过y[k]可以很快推出r的值。事实上，y[k]可以通过递推在O(n)时间内解决：

for (int j=0; j<= x[i-2]*(m-1);j++)
        if (y[j]<m)
          for (int k=1;k<=m-y[j];k++)
            if (y[j]+k<y[j+x[i-1]*k]) y[j+x[i-1]*k]=y[j]+k;
      while (y[r]<maxint) r++;

---

八、回溯法效率分析

  通过前面具体实例的讨论容易看出，回溯算法的效率在很大程度上依赖于以下因素：
  (1)产生x[k]的时间；
  (2)满足显约束的x[k]值的个数；
  (3)计算约束函数constraint的时间；
  (4)计算上界函数bound的时间；
  (5)满足约束函数和上界函数约束的所有x[k]的个数。
  好的约束函数能显著地减少所生成的结点数。但这样的约束函数往往计算量较大。因此，在选择约束函数时通常存在生成结点数与约束函数计算量之间的折衷。

---

九、重排原理

  对于许多问题而言，在搜索试探时选取x[i]的值顺序是任意的。在其它条件相当的前提下，让可取值最少的x[i]优先。从图中关于同一问题的2棵不同解空间树，可以体会到这种策略的潜力。


  图(a)中，从第1层剪去1棵子树，则从所有应当考虑的3元组中一次消去12个3元组。对于图(b)，虽然同样从第1层剪去1棵子树，却只从应当考虑的3元组中消去8个3元组。前者的效果明显比后者好。

---

十、回溯法的效率分析

  解空间的结构一经选定，影响回溯法的前三个因素就可以确定
  生成结点的数目是可变的（做文章）
  当问题实例的规模n较大时，回溯法能用很少的时间求得问题的解
  很难估计出回溯法在解具体实例时所产生的结点数
  但有近似估计的方法，准确度相当高

---

十一、Monte Carlo方法

  从根开始，随机选择一条路径，直到不能分支为止。即从x1,x2,…,依次对xi赋值，每个xi的值是从当时的Si中随机选取，直到向量不能扩张为止
  假定搜索树的其它|Si|-1个分支与以上随机选出的路径一样，计数搜索树的点数。
  重复上两个步骤，将结点数进行概率平均

---

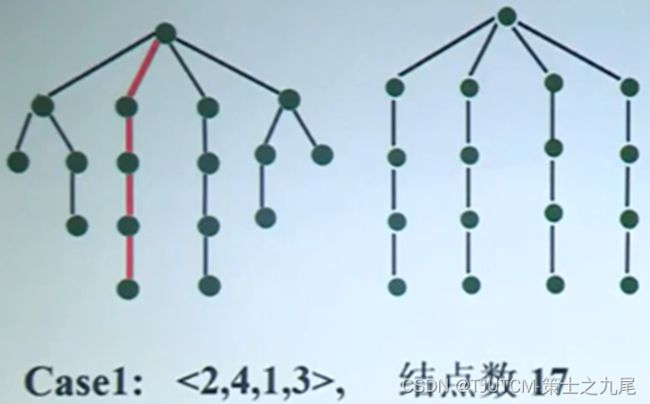
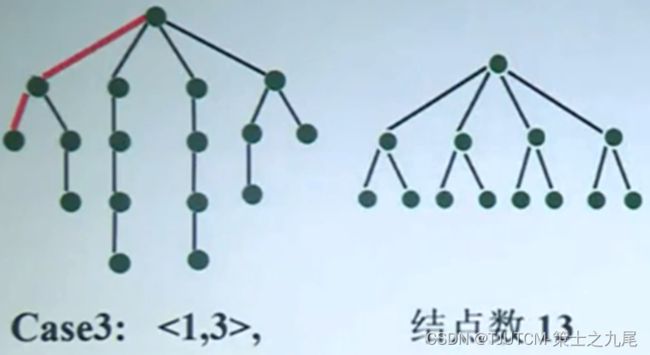
附一、四后问题的搜索树

  只需访问17个结点

---

附二、随机选择路径

---

附三、估计结果

  假设4次抽样测试：
  Case1:1次
  Case2:1次
  Case3:2次
  平均结点数=（211+171+13*2）/4=16
  非常接近搜索空间访问的真正结点数17
  17/4^4=17/256=6.64%，即93%的其它结点都被剪枝后裁去了！

---

十一、小结

  适于求解组合搜索问题及优化问题
  求解条件：满足多米诺性质。
  解的表示：解向量，求解是不断扩充解向量的过程
  回溯条件：
  搜索问题——约束条件
  优化问题——约束条件+代价函数
  分支策略：深度优先

  结点状态：白结点，黑结点，灰结点
  算法时间复杂度：O(2n)或O(n!)
  平均时间复杂度和空间复杂度较低
  降低时间复杂度的主要途径：
  根据树的分支设计优先策略，结点少分支优先，或解多的分支优先
  利用搜索树的对称性裁剪子树
  分解为子问题（略）。