算法分析与设计：回溯法

1、回溯法

回溯法有“通用解题法”之称，是一种系统地搜索答案的解答方法。

● 基本思想

回溯法为问题定义一个解空间，该空间至少包含问题的一个解，并可以组织成一棵树；在解空间树中，以深度优先策略搜索，判断当前结点是否包含问题的解：如果不包含，则跳过该结点，回到祖先节点，称为回溯；如果包含，则继续以深度优先策略进行搜索，进入该结点的子树。
回溯法的基本思想可以概括为：能进则进，不能进则回。

为使用回溯法解决问题，首先要确定搜索范围，这需要明确以下几个方面：
● 问题的解向量：回溯法的解可以表示为一个n元组(x₁,x₂,…,x_n)；
● 问题的解空间：满足显式约束的解向量组构成一个解空间。回溯法的解空间可以组织成一棵树；
● 问题的可行解：解空间中满足隐式约束的解向量就是一个可行解；
● 问题的最优解：对问题给定的目标，所有可行解中目标达到最优的可行解；
● 显式约束：解向量的分量x_i的取值范围；
● 隐式约束：问题给定的约束条件。

● 典型解空间树

解空间通常有两种典型的解空间树：

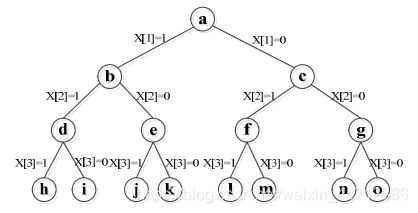
1. 子集树

从n个物体的集合r中选择满足某种性质的子集，这类问题的解空间树称为子集树。n个物品集合的子集个数为2ⁿ。
解向量：对于n个物品的集合，其解向量也有n个分量，可表示为(x₁,x₂,…,x_n)。
显式约束：对于子集树问题，通常取x_i∈{0,1}，其中0表示物体不在解向量对应的子集中；1表示物体在解向量对应的子集中。
隐式约束：由问题决定。例如0-1背包问题中为：子集中的物体总重量不超过背包的容量。
显然子集树是一棵满二叉树，其结点总数为：2ⁿ⁺¹-1。遍历的时间复杂度为O(2ⁿ)。

2. 排序树

从n个元素的集合r中找出满足某种性质的排列，这类问题的解空间树称为排列树。n个元素集合的排列个数为n!。
解向量：对于n个元素的集合，其解向量也有n个分量，可表示为(x₁,x₂,…,x_n)。
显式约束：对于排列树问题，有x_i∈r，且对任意的i≠j，都有x_i≠x_j。
隐式约束：由问题决定。
排列树的每一个结点的子节点个数都为它所在层次的结点个数-1，叶子结点总数为n!。遍历的时间复杂度为O(n!)。

解空间树的结点表示的是一种状态，而边表示解向量分量的取值。

● 解空间的搜索

回溯法从根节点出发，以深度优先搜索方式搜索整个解空间树。
● 活结点：还有子节点未生成的结点，称为活结点
● 死结点：不能进一步扩展，或者说所有子节点都已经生成的结点，称为死结点
● 扩展结点：当前正在生成子节点的结点，称为扩展结点

死结点不仅包括受隐式约束影响而不能生成子结点的结点，也包括已经完成遍历的结点；当所有结点都成为死结点时，回溯法搜索结束。

不同于普通的穷举法，回溯法在搜索时使用两种策略避免无效搜索：
● 约束函数：在扩展结点处删去不满足结束条件的子树
● 限界函数：剪去不能得到最优解的子树
这两类函数统称为剪枝函数。

由于剪枝，回溯法具体问题时消耗的时间会比理论最坏情况下计算的时间复杂度要低，有些场合甚至低得多。

● 基本步骤

综上讨论，回溯法包含三个步骤：

1. 针对问题，给出解空间
2. 确定解空间组织结构
3. 深度优先搜索解空间，并使用剪枝函数避免不必要的搜索

用深度优先思想完成回溯的完整过程如下：

1. 初始化设置，找到根节点作为扩展结点
2. 判断扩展结点是否是叶子节点。若是，转到6
3. 利用约束函数，试探未遍历的子节点；若试探结束(没有未遍历的子节点)，转到7
4. 若试探成功，以更新扩展结点，回到2
5. 若试探失败，回到3
6. 找到可行解，记录解向量
7. 回溯到父节点，回到3；若没有父节点(退到头)，结束搜索

2.经典问题

● M着色问题

1. 问题描述
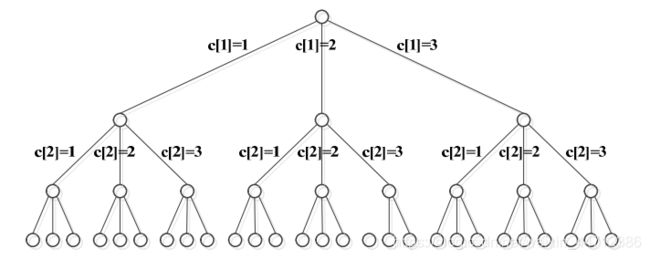
   给定一个有n个顶点的无向图G={V,E}和m种不同的颜色。用这m种颜色为顶点上色，使相邻的顶点颜色不同。
2. 问题的解空间
   解向量C的长度为n，其中C[i]∈{1,2,…,m}。该问题的解空间是一棵完全三叉树，如下图。
   从根节点到叶子节点的一条路径就是问题的一个解向量。
   
3. 约束条件
   检查当前顶点与所有邻接顶点的颜色是否相同，如果相同说明该颜色不可行，进行剪枝。
4. 算法流程
   ● 从起始状态(所有顶点未被着色)出发，逐个顶点着色
   ● 为顶点逐个试探颜色，判断该颜色是否可用
   ● 如颜色可用，成功着色并继续为下一个顶点进行着色
   ● 如成功着色且该顶点为最后一个(叶子节点)，记录当前的解向量，并试探其它颜色
   ● 如颜色不可用，更换颜色并再次试探
   ● 若所有颜色都被试探过，回到上一个结点，对其它颜色进行试探
5. 算法实现

//M着色问题
//n为顶点个数
//a为邻接矩阵，ans为解向量，v为当前顶点，vNum = n，colorNum为颜色种数，res记录所有可行解
//#define NUM x	其中x = vNum

bool isAvailableColor(int a[NUM][NUM], int *ans, int vNum, int v)    //判断颜色是否可用
{
    for(int i = 0;i < vNum;i++){
        if(a[v][i] == 1 && ans[v] == ans[i])    //邻接且颜色相同为非法
            return false;
    }
    return true;
}

void mColor(int a[vNUM][NUM], int *ans, int vNum, int v, int colorNum, vector<int*> &res)     //M着色递归算法
{

    if(v >= vNum){      //递归出口
        int *new_ans = new int[vNum];
        for(int i = 0;i < vNum;i++)
            new_ans[i] = ans[i];
        res.push_back(new_ans);
    }
    else{
        for(int i = 1;i <= colorNum;i++){           //遍历每一个颜色
            ans[v] = i;
            if(isAvailableColor(a,ans,v,vNum))      //约束条件
                mColor(a,ans,v+1,vNum,colorNum,res);
            ans[v] = 0;			//回溯，还原解向量
        }
    }
}

最坏情况下需要遍历mⁿ个解向量，每遍历一个结点就需要进行一次n步的判断。时间复杂度为O(n·mⁿ)。

● N皇后问题

1. 问题描述
   在n×n的棋盘上摆放n个皇后，求 使得皇后之间不能互相攻击 的摆法。
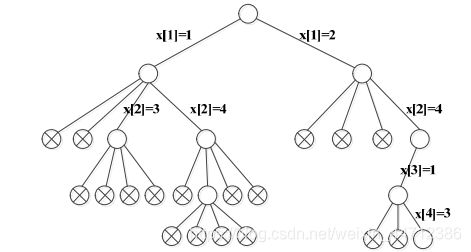
   Tip：国际象棋中，皇后可以攻击同列、同行和同对角线的棋子。
2. 问题的解空间
   皇后之间不得互相攻击，显然皇后必然放在不同的行中。为摆放在各行的皇后编号为{0,1,2,…,n-1}。
   同样的，皇后也必然放在不同的列中；若第一个皇后有n中摆放方式，则第i个皇后有n - i + 1种摆放方式。
   解向量X的长度为n，其中X[i]∈{1,2,…,n}，满足X[i] ≠ X[j] ( if i ≠ j )。
   因此，N皇后问题的解空间实质上是一棵排列树。
   
3. 约束条件
   首先，我们已经规定了各皇后不在同一行中。
   其次，我们需要确定各皇后不在同一列中，即X[i] ≠ X[j]。
   最后，我们需要确定各皇后不在同一对角线上，即 |X[i] - X[j]| ≠ |i - j|。
4. 算法流程
   ● 从起始状态开始，为所有皇后确定位置
   ● 试探皇后的位置，判断该位置是否可用
   ● 若位置可用，成功确定位置并确定下一个皇后的位置
   ● 若成功确定位置且该皇后是最后一个，记录当前解向量，并试探其它位置
   ● 若位置不可用，更换位置再次试探
   ● 若所有位置都试探过，回到上一个结点，对其它位置进行试探
5. 算法实现

//N皇后问题
//n为棋盘的大小和皇后的个数，i为当前皇后的编号，ans为当前解向量，res记录所有可行解

bool isAvailablePos(int i, int *ans)    //判断位置是否可用
{
    for(int j = 0;j < i;j++){   //只有前i个皇后确定了位置，无需考虑后面的皇后
        if(ans[i] == ans[j] || abs(ans[i] - ans[j]) == abs(i - j))
            return false;
    }
    return true;
}

void nQueen(int n, int i, int *ans, vector<int*> &res)     //N皇后递归算法
{
    if(i >= n){             //递归出口
        int *new_ans = new int[n];
        for(int j = 0;j < n;j++)
            new_ans[j] = ans[j];
        res.push_back(new_ans);
    }
    else{
        for(int j = 0;j < n;j++){       //遍历所有位置
            ans[i] = j + 1;
            if(isAvailablePos(i,ans))   //约束条件
                nQueen(n,i+1,ans,res);
            ans[i] = 0;
        }
    }
}

理论最坏情况下需要遍历nⁿ个解向量，时间复杂度为O(nⁿ)。但由于约束条件2，实际最坏时间消耗n!。再加上约束条件3，实际的平均时间消耗更低。

● 两船装载问题

1. 问题描述
   有n个集装箱要装上2艘载重分别为C₁，C₂的轮船，第i个集装箱的重量为w[i]。找出一种能将所有集装箱装入的装载方案。

2. 问题的解空间
   首先分析问题，如果船1能够装尽可能多的集装箱，那剩余的重量就会变少，更有可能将集装箱完全装入。
   得到上面问题的最优解后，判断剩余的集装箱能否全部装入船2，如能则得到解；否则问题无解。
   解向量X的长度为n，其中X[i]∈{0,1}。0表示不装入船1，1表示装入船1。
   因此，该问题的解空间为子集树。
   

3. 约束条件
   检查货物能否装入船1中，如果能说明该子树的解向量可能可行；否则不可行，进行剪枝。

不同于前面的例题，子集树问题总是有可以前进的方向，为了避免得出无意义的解向量，需要添加限界条件。

4. 限界条件
   为了得到船1的最优解，我们还需要限界条件。
   如果货物不能装入，判断剩余的最大重量(当前载重C_w+剩余重量R_w)是否小于最优值(找到的最大重量)；若是，进行剪枝。
5. 算法流程
   ● 从起始状态开始，逐个判断集装箱能否装入船1中
   ● 如果能装入，将集装箱装入，更新当前重量
   ● 如果不能装入，跳过该集装箱，计算剩余的最大重量是否小于最优解，若是则进行剪枝，回溯到上一结点
   ● 判断下一个集装箱是否能够装入
   ● 若已经是最后一个集装箱，与最优解进行比较；若该解更优，更新最优解
6. 算法实现

//两船装载问题
//w为集装箱重量序列，n为集装箱个数，i为当前集装箱序号，cw为当前已装载量,c1为1船最大载重
//w为当前可行值，ans为当前可行解
//W为最优值(1船最大装载重量)，ANS为最优解

int W = 0;
int *ANS;   //获取n后分配空间
int bound(int *w, int n, int i, int cw)   //限界条件
{
    int rw = 0;
    for(int j = i;j < n;j++)    //剩余最大重量
        rw += w[i];
    return rw + cw;         //可能的最大重量
}

bool isAvailableContainer(int *w, int i, int cw, int c1)   //约束条件
{
    if(cw + w[i] > c1)
        return false;
    return true;
}

void doubleCruiseLoad(int *w, int n,int i, int cw, int c1, int *ans)  //两船装载递归算法
{
    if(i >= n){     //递归出口
        if(cw > W){ //更新最优解
            W = cw;
            for(int i = 0;i < n;i++)
                ANS[i] = ans[i];
        }
    }
    else{
        if(isAvailableContainer(w,i,cw,c1)){		//可以装入
            ans[i] = 1;
            doubleCruiseLoad(w,n,i+1,cw+w[i],c1,ans);	//装入
            ans[i] = 0;
        }
        if(bound(w,n,i,cw) > W){		//满足限界条件，可以不装入
            doubleCruiseLoad(w,n,i+1,cw,c1,ans);		//不装入
        }
    }
}

由于这是一个子集树，其解向量共有2ⁿ个。时间复杂度为O(2ⁿ)。

● 旅行商问题

1. 问题描述
   又称TSP问题。一个旅行商从起点出发，经过所有给定的n个城市(包括起点)并回到起点，求旅行商走过的最短路径。
2. 问题的解空间
   解向量X的长度为n，其中X[i]∈{1,2,…,n}，满足X[i] ≠ X[j] ( if i ≠ j )。该问题的解空间是一个典型的排列树。
   
3. 约束条件
   对于所有未被选择的结点，必须满足本结点到目标结点之间存在路径。即a[i][i-1] > 0，并且最后一个顶点必须与第一个顶点相连，即a[n-1][0] > 0。
4. 限界条件
   设cl为当前已走过的路径长度，ml为已找到的最短路径长度。显然当cl > ml时，该路径不可能得到最优解，进行剪枝。
5. 算法流程
   ● 从初始状态(未经过任意城市)开始
   ● 如果指定了起点，从起点开始；否则在所有城市中选择一个起点
   ● 试探剩余的顶点，判断顶点是否可达
   ● 如果顶点可达，到达该顶点并判断当前路径长度是否大于最优值；若是则进行剪枝，回溯到上一结点
   ● 试探剩余结点是否可达
   ● 若已经是最后一个顶点，判断是否可以回到起点。若不能，进行剪枝；
   ● 若得到可行解，判断是否优于当前最优解，若是，更新最优解。
6. 算法实现

//旅行商问题
//n为城市数，a为邻接矩阵,ans为当前可行解，cl为当前路径长度,i为当前递归次数
//minLength为当前最优值，ANS为当前最优解
//全局变量获取n后赋值，最优值初设为最大
//#define NUM x 其中x = n

int minLength = 0x7fffffff;
int *ANS;
//注：C++的二维数组传参较为麻烦，如不能事先给定NUM，考虑使用全局变量
bool isAccessible(int a[NUM][NUM], int n, int *ans, int i)    //约束条件
{
    if(i == 0)  return true;    //选取入口，无需判断可达
    else if(i == n && a[ans[0]][ans[i-1]] > 0)     //最后一个顶点，判断能否回到入口
        return true;
    else if(a[ans[i-1]][ans[i]] > 0)
        return true;
    return false;
}

void travelBussiness(int a[NUM][NUM], int n, int *ans, int cl, int i)    //旅行商问题递归算法，如给定起点，i从1开始
{
    if(i >= n){     //递归出口
        if(cl < minLength && isAccessible(a,n,ans,i)){
            minLength = cl;
            for(int j = 0;j < n;j++)
                ANS[j] = ans[j];
        }
    }
    else{
        for(int j = i;j < n;j++){
            swap(ans[i],ans[j]);			//ans存储顶点的编号，选择一个顶点后，做顶点交换，表示先经过该顶点
            								//交换后，i之后的顶点为未被选择的剩余顶点
            if(isAccessible(a,n,ans,i)){   //约束条件
                if(i > 0)					//起点位置不进行路径叠加
                    cl += a[ans[i-1]][ans[i]];
                if(cl < minLength)                      //限界条件
                    travelBussiness(a,n,ans,cl,i+1);
                if(i > 0)
                    cl -= a[ans[i-1]][ans[i]];
            }
            swap(ans[i],ans[j]);         //回溯
        }
    }
}

这是一个典型的排列树问题，共有n!个解向量，时间复杂度为O(n!)。