掌握imgproc组件：opencv-图像处理

1.线性滤波：方框滤波、均值滤波、高斯滤波

1.1 平滑处理

平滑处理(smoothing)也成为模糊处理(bluring)，是一种简单且使用频率很高的图像处理方法。平滑处理的用途有很多，最常见的是用来减少图像上的噪点或者失真。在涉及到降低图像分辨率时，平滑处理是非常好用的方法。

1.2 图像滤波与滤波器

图像滤波，指在尽量保留图像细节特征的条件下对标图像的噪声进行抑制，是图像预处理中不可缺少的操作，其处理效果的好坏将直接影响到后续图像处理和分析的有效性和可靠性。

消除图像中的噪声成分叫做图像的平滑化或者滤波操作。信号或图像的能量大部分集中在幅度谱的低频和中频段，有用的信息经常被噪声淹没。因此一个能降低高频成分幅度的滤波器就能够减少噪声的影响。

图像滤波的目的有两个：一个是抽出对象的特征作为图像识别的特征模式；另一个是为适应图像处理的要求，消除图像数字化时所混入的噪声。

而对滤波处理的要求也有两条：一是不能损坏图像的轮廓及边缘等重要信息；二是使图像清晰视觉效果好。

平滑滤波是低频增强的空间域滤波技术。它的目的有两类：一类是模糊；另一类是消除噪音。

空间域的平滑滤波一般才用简单平均法进行，就是求邻近像元点的平均亮度值。邻域的的大小与平滑的效果直接相关，邻域越大平滑的效果越好，但邻域过大，平滑也会使边缘信息损失的越大，从而使输出的图像变得模糊，因此需合理选择邻域的大小。

关于滤波器，一种形象的比喻就是：可以把滤波器想象成一个包含加权系数的窗口，当使用这个滤波器平滑处理图像时，就把这个窗口放到图像上，透过这个窗口来看我们得到的图像。

滤波器的种类有很多：

• 方框滤波——BoxBlur函数
• 均值滤波——Blur函数
• 高斯滤波——GaussianBlur函数
• 中值滤波——medianBlur函数
• 双边滤波——bilateralFilter函数

1.3 线性滤波器的简介

线性滤波器经常用于提出输入信号中不想要的频率或者从许多频率中选择一个想要的频率。

• 低通滤波器：允许低频率通过
• 高通滤波器：允许高频率通过
• 带通滤波器：允许一定范围频率通过
• 带阻滤波器：阻止一定范围频率通过并且允许其他频率通过
• 全通滤波器：允许所有频率通过，仅仅改变相位关系
• 陷波滤波器：阻止一个狭窄频率范围通过，是一种特殊的带阻滤波器。

1.4 滤波和模糊

滤波是将信号中特定波段频率滤除的操作，是防止和抑制干扰的一项重要措施。
以高斯滤波为例：滤波可分为低通滤波和高通滤波两种：高斯滤波是指用高斯函数作为滤波函数的滤波操作，至于是不是模糊，就要看是高斯低通还是高斯高通，低通就是模糊，高通就是锐化。

1.5 邻域算子与线性邻域滤波

邻域算子（局部算子）是利用给定像素周围的像素值的决定此像素的最终输出值的一种算子。而线性邻域滤波就是一种常用的邻域算子，像素的输出值取决于输入像素的加权和。

邻域算子除了用于局部色调调整以外，还可以用于图像滤波，以实现图像的平滑和锐化、图像边缘增强或者图像噪声的去除。

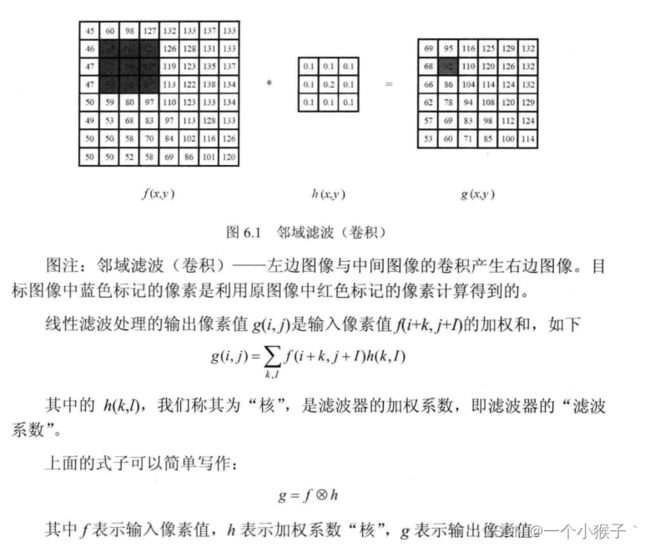
1.6 方框滤波

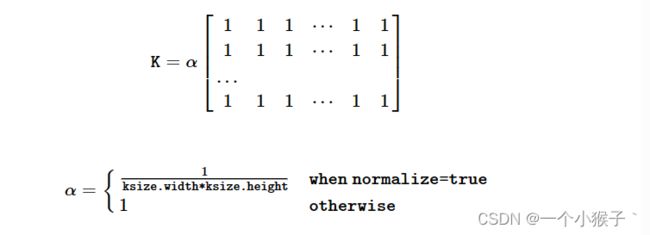
方框滤波被封装在一个名为boxblur的函数中，即boxblur函数的作用是使用方框滤波器来模糊一行图片
void boxFilter(InputArray src, OutputArray dst, int ddepth, Size ksize, Point anchor=Point(-1,-1), bool normalize=true, int borderType=BORDER_DEFAULT)

• 第一个参数：输入图像
• 第二个参数：输出图像，与源图像有一样的尺寸和类型
• 第三个参数：输出图像的深度，-1代表使用原图深度
• 第四个参数：内核的大小
• 第五个参数：锚点；默认值Point(-1,-1)表示锚点在内核中心。
• 第六个参数：指定内核是否按其区域进行归一化。
• 第七个参数：用于推断图像外部像素的某种边界模式。

boxFilter()函数方框滤波所用的核表示如下：

1.7 均值滤波

均值滤波，是最简单的一种滤波操作，输出图像的每一个像素是核窗口内输入图像对应像素的平均值。其实说白了它就是归一化后的方框滤波。

均值滤波的缺陷
均值滤滤波本身存在着固有的缺陷，即它不能很好地保护图像细节，在图像去噪的同时也破坏了图像的细节部分，从而使图像变得模糊，不能很好地去除噪声点。

void blur(InputArray src, OutputArray dst, Size ksize, Point anchor=Point(-1,-1),int borderType=BORDER_DEFAULT)
参数可参考方框滤波。

1.8 高斯滤波

void GaussianBlur(InputArray src, OutputArray dst, Size ksize, double sigmaX, double sigmaY=0, int borderType=BORDER_DEFAULT)

• 第一个参数：输入图像；该图像可以有任何数量的通道，它们被独立处理，但深度应该是CV_8U、CV_16U、CV_16S、CV_32F或CV_64F。
• 第二个参数：输出图像
• 第三个参数：高斯内核的大小
• 第四个参数：表示高斯核函数在X方向的标准偏差
• 第五个参数：Y方向的高斯核标准差；如果sigmaY为零，则设置为等于sigmaX，如果两个sigmas都为零，则分别从ksize.width和ksize.height中计算出来。
• 第六个参数：用于推断图像外部像素的某种边界模式。有默认值BORDER_DEFAULT，我们一般不去管它。

深度的概念
图像深度是指存储每个像素所用的位数,也用于量度图像的色彩分辨率.图像深度确定彩色图像的每个像素可能有的颜色数,或者确定灰度图像的每个像素可能有的灰度级数。他决定了彩色图像中可出现的最多颜色数，或灰度图像中的最大灰度等级。

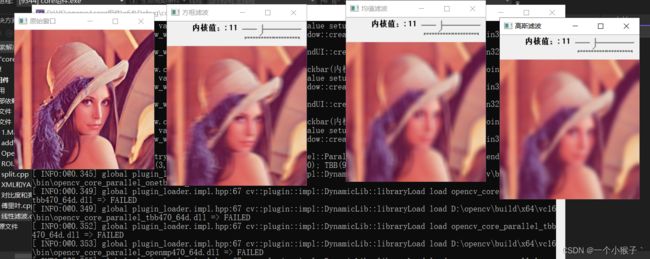
1.9 线性滤波综合案例

#include
using namespace std;
using namespace cv;

//-----------------全局变量声明-------------------
Mat g_srcImage, g_dstImage1, g_dstImage2, g_dstImage3;//存储图
int g_nBoxFilterValue = 3; //方框滤波参数值
int g_nMeanBlurValue = 3;//均值滤波参数值
int g_nGaussianBlurValue = 3;//高斯滤波参数值

//方框滤波操作的回调函数
static void on_BoxFilter(int, void*) {
	boxFilter(g_srcImage, g_dstImage1, -1, Size(g_nBoxFilterValue + 1, g_nGaussianBlurValue + 1));
	imshow("方框滤波", g_dstImage1);
}

//均值滤波的回调函数
static void on_MeanBlur(int, void*) {
	blur(g_srcImage, g_dstImage2, Size(g_nMeanBlurValue + 1, g_nMeanBlurValue + 1));
	imshow("均值滤波",g_dstImage2);
}

//高斯滤波
static void on_GaussianBlur(int, void*) {
	GaussianBlur(g_srcImage, g_dstImage3, Size(g_nGaussianBlurValue * 2 + 1, g_nGaussianBlurValue * 2 + 1), 0, 0);
	imshow("高斯滤波", g_dstImage3);
}

int main() {
	g_srcImage = imread("../../image/lena_color_256.tif");
	if (!g_srcImage.data)  cout << "图片读取错误" << endl;

	//赋值原图到三个Mat类型中
	g_dstImage1 = g_srcImage.clone();
	g_dstImage2 = g_srcImage.clone();
	g_dstImage3 = g_srcImage.clone();
	
	namedWindow("原始窗口");
	imshow("原始窗口",g_srcImage);

	namedWindow("方框滤波");
	createTrackbar("内核值：","方框滤波",&g_nBoxFilterValue,40,on_BoxFilter);
	on_BoxFilter(g_nBoxFilterValue, 0);


	namedWindow("均值滤波");
	createTrackbar("内核值：", "均值滤波", &g_nMeanBlurValue, 40, on_MeanBlur);
	on_MeanBlur(g_nMeanBlurValue, 0);

	namedWindow("高斯滤波");
	createTrackbar("内核值：", "高斯滤波", &g_nGaussianBlurValue, 40, on_GaussianBlur);
	on_GaussianBlur(g_nGaussianBlurValue, 0);

	waitKey();
	return 0;
}

2.非线性滤波：中值滤波、双边滤波

2.1 中值滤波

中值滤波是一种典型的非线性滤波技术，基本思想是用像素点邻域灰度值的中值来代替像素点的灰度值，该方法在去除脉冲噪声、椒盐噪声的同时又能保留图像的边缘细节。
中值滤波是基于排序统计理论的一种能够有效抑制噪声的非线性信号处理技术，其基本原理是把数字图像或数字序列中一点的值用该店的一个林与众个点至的中值代替，该周围的像素值接近真实值，从而消除孤立的噪声点。这对于斑点噪声和椒盐噪声来说尤其有用，因为他不依赖于邻域内那些典型值差别很大的值。中值滤波器在处理连续图像窗函数时与线性滤波器的工作方式类似，但滤波过程不再是加权运算。
中值滤波在一定的条件下可以克服常见线性滤波器，如最小均方滤波、方框滤波、均值滤波等带来的图像细节模糊，而且对滤除脉冲干扰及图像扫描噪声非常有效，也常用于保护边缘信息。保存边缘的特征使它在不希望出现边缘模糊的场合也很有用，是非常经典的平滑噪声处理方式。

中值滤波与均值滤波器比较
优势：在均值滤波器中，由于噪声成分被放入平均计算中，所以输出受到了噪声的影响。但是在中值滤波器中，由于噪声成分很难被选上，所以几乎不会影响到输出。因此同样用33区域进行处理，中值滤波消除的噪声能力更胜一筹。中值滤波无论是在消除噪声还是保存边缘方面都是一个不错的方法。
劣势：中值滤波花费的时间是均值滤波的5倍以上。
顾名思义，中值滤波选择每个像素的邻域像素中的中值作为输出，或者说中值滤波将每一像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值。
例如，去33的函数窗，计算以点[i,j]为中心的函数窗像素中值，具体步骤如下。
1）按强度值大小排列像素点
2）选择排序像素集的中间值作为点[i,j]的新值。
一般采用奇数点的邻域来计算中值，但像素点数为偶数时，中值就取排列像素中间两个点的平均值。

中值滤波在一定条件下，可以克服线性滤波器(如均值滤波等)所带来的图像细节模糊，对滤除脉冲干扰即图像扫描噪声最为有效，而且在实际运算过程中并不需要图像的统计特性，也给计算带来不少方便。但是对一些细节(特别是细、尖顶等)多的图像不太适合。

void medianBlur(InputArray src, OutputArray dst, int ksize)

• 第一个参数：填1、3或者4通道的Mat类型图像。当ksize为3或者5的使用，图像深度需为CV_8U、CV_16U、CV_32F其中之一，而对于较大孔径尺寸的图片，它只能是CV_8U。
• 第二个参数：函数的输入参数，需要和源图片有一样的尺寸和类型。我们可以用Mat::Clone，以源图片为模板，来初始化得到如假包换的目标图。
• 第三个参数：int类型的ksize，孔径的线性尺寸，注意这个参数必须是大于1的奇数。

2.2 双边滤波

双边滤波是一种非线性的滤波方法，是结合图像的空间邻近度和像素值相似度的一种折中处理，同时考虑空域信息和灰度相似性，达到保边去噪的目的，具有简单、非迭代、局部的特点。
双边滤波器的好处是可以做边缘保存。以往常用维纳滤波或者高斯滤波去降噪，但二者都会较明显地模糊边缘，对于高频细节的保护效果并不明显。双边滤波器顾名思义，比高斯滤波多了一个高斯方差sigma-d，它是基于空间分布的高斯滤波函数，所以在边缘附近，离得较远的像素不会对边缘上的像素值影响太多，这样就保证了边缘附近像素值的保存。但是，由于保存了过多的高频信息，多余彩色图像里的高频噪声，双边滤波器不能够干地滤掉，知识对于低频信息系进行了比较好的滤波。
void bilateralFilter(InputArray src, OutputArray dst, int d, double sigmaColor, double sigmaSpace, int borderType=BORDER_DEFAULT)

• 第一个参数：输入图像，需要为8位或者浮点型单通道、三通道图像。
• 第二个参数：输出图像，需要和源图像有一样的类型和尺寸。
• 第三个参数：表示在过滤过程中每个像素邻域的直径。如果这个值被设置为非正数，那么OpenCV会从第五个参数sigmaSpace计算出来它。
• 第四个参数：颜色空间滤波器的sigma值。这个参数的值越大，就表明该像素淋浴呢优越宽广的颜色会被混合到一起，产生较大的半相等颜色区域。
• 第五个参数：坐标空间中滤波器的是sigma值，坐标空间的标注方差。它的数值越大，意味着越远的像素会相互影响，从而使更大的区域中足够相似的颜色获取相同的颜色。当d>0，d指定了邻域大小且与sigmaSpace无缘。否则d正比于sigmaSpace。
• 第六个参数：用于推断图像外的像素的边界模式。

2.3 综合案例

#include
using namespace std;
using namespace cv;

Mat srcImage, dstImage1, dstImage2;
int g_nMedianBlurValue = 10; //中值滤波参数值
int g_nBilateralFilterValue = 10;//双边滤波参数值

//中值滤波操作的回调函数
static void on_MedianBlur(int, void*) {
	medianBlur(srcImage, dstImage1, g_nMedianBlurValue * 2 + 1);
	imshow("中值滤波", dstImage1);
}

//双边滤波操作的回调函数
static void on_BilateralFilter(int, void*) {
	bilateralFilter(srcImage, dstImage2, g_nBilateralFilterValue, g_nBilateralFilterValue * 2, g_nBilateralFilterValue / 2);
	imshow("双边滤波", dstImage2);
}


int main() {
	srcImage = imread("../../image/1.tif");
	if (!srcImage.data) {
		cout << "图片读入错误" << endl;
		return false;
	}
	dstImage1 = srcImage.clone();
	dstImage1 = srcImage.clone();
	namedWindow("原图", 0);
	imshow("原图", srcImage);

	//中值滤波
	namedWindow("中值滤波", 0);
	createTrackbar("参数值：", "中值滤波", &g_nMedianBlurValue, 50, on_MedianBlur);
	on_MedianBlur(g_nMedianBlurValue, 0);
	
	//双边滤波
	namedWindow("双边滤波", 0);
	createTrackbar("参数值：", "双边滤波", &g_nBilateralFilterValue, 50, on_BilateralFilter);
	on_BilateralFilter(g_nBilateralFilterValue, 0);

	waitKey();
	return 0;

}

3.形态学滤波(1):腐蚀与膨胀

形态学操作就是基于形状的一系列图像处理操作。最基本的形态学操作有两种，分别是：膨胀与腐蚀。
膨胀与腐蚀能实现多种多样的功能，主要如下。

• 消除噪声
• 分割出独立的图像元素，在图像中连接相邻的元素
• 寻找图像中的明显的极大值区域和极小值区域
• 求出图像的梯度

3.1 膨胀

膨胀（dialate）就是求局部最大值的操作。从数学角度来说，膨胀或者腐蚀操作就是将图像与核进行卷积。
核可以死任何形状和大小，它拥有一个单独定义出来的参考点，我们称其为锚点。多数情况下，核实一个小的，中间带有参考点和实心正方形或者圆盘。其实，可以把核视为模板或者掩码。
而膨胀就是求局部最大值的操作。核与图形卷积，计算核覆盖的区域的像素点的最大值，并把这个最大值赋值给参考点指定的像素。这样就会使图像中的高亮区域逐渐增长。

• 第一个参数：输入图像
• 第二个参数：输出图像和源图像有桐乡的类型和尺寸
• 第三个参数：用于膨胀操作的核；如果 element=Mat()，则使用一个 3 x 3 的矩形结构元素。一般使用getStructuringElement函数配合这个参数使用。geiStructuringElement函数会返回指定形状和尺寸的结构元素。其中，getStructuringElement函数的第一个参数表示内核的形状。第二个和第三个参数分别是内核尺寸以及锚点的位置。
• 第四个参数：锚点在元素中的位置；默认值（-1，-1）意味着锚点位于元素中心。
• 第五个参数：迭代使用dilate()函数的次数
• 第六个参数：用于推断图像外部像素的某种边界模式
• 第七个参数：const Scalar&类型的borderType，用于推断图像外部像素的某种边界模式。
  使用dilate函数，一般只需要填前面的三个参数，后面的四个参数都有默认值，而且往往结合getStructuringElement一起使用。

3.2 腐蚀

膨胀和腐蚀(erode)是相反的一对操作，所以腐蚀就是求局部最小值的操作。

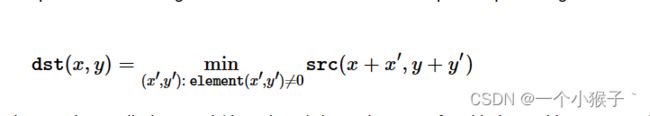
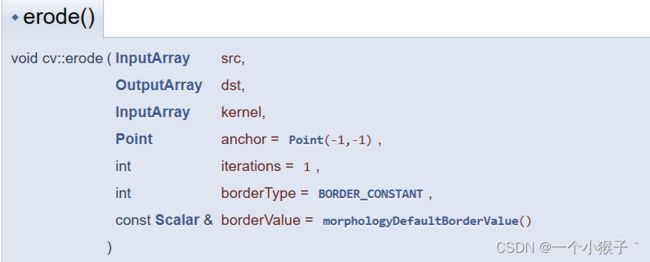
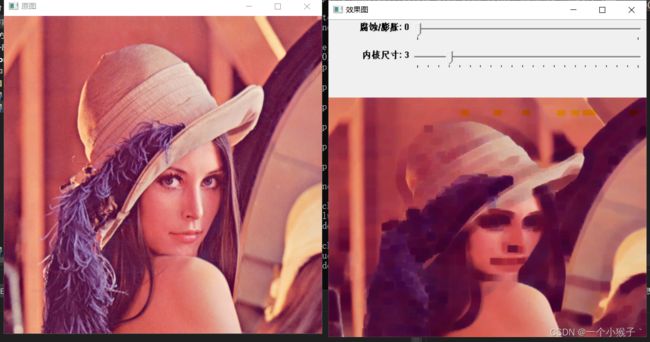
3.3 腐蚀和膨胀综合案例

#include
using namespace std;
using namespace cv;

Mat srcImage, dstImage;
int g_nTrackbarNumer = 0;//0表示腐蚀，1表示膨胀
int g_nStructElementSize = 3;//结构元素的尺寸

//进行自定义的腐蚀和膨胀操作
void Process() {
	Mat element = getStructuringElement(MORPH_RECT, Size(2 * g_nStructElementSize * 2 + 1, 2 * g_nStructElementSize * 2 + 1),
		Point(g_nStructElementSize, g_nStructElementSize));

	if (g_nTrackbarNumer == 0)
		erode(srcImage, dstImage, element);
	else
		dilate(srcImage, dstImage, element);

	imshow("效果图", dstImage);
}

//膨胀和腐蚀之间切换开关的回调函数
void on_TrackbarNumChange(int, void*) {
	Process();
}

//膨胀和腐蚀操作内核改变时的回调函数
void on_ElementSize(int, void*) {
	Process();
}

int main() {
	srcImage = imread("../../image/1.tif");
	if (!srcImage.data) {
		cout << "读取图片错误" << endl;
		return false;
	}
	namedWindow("原图",0);
	imshow("原图", srcImage);

	namedWindow("效果图", 0);

	Mat element = getStructuringElement(MORPH_RECT,
		Size(2 * g_nStructElementSize + 1, 2 * g_nStructElementSize * 2 + 1),
		Point(g_nStructElementSize, g_nStructElementSize));
	erode(srcImage, dstImage, element);
	imshow("效果图", dstImage);

	//创建轨迹条
	createTrackbar("腐蚀/膨胀", "效果图", &g_nTrackbarNumer, 1, on_TrackbarNumChange);
	createTrackbar("内核尺寸", "效果图", &g_nStructElementSize, 21, on_ElementSize);
	
	waitKey();
	return 0;
}

4.形态学滤波(2):开运算、闭运算、形态学梯度、顶帽、黑帽

本节的主角是OpenCV中的morphologyEx函数，他利用基本的膨胀和腐蚀技术，来执行更加高级的形态学变换，如开闭运算、形态学梯度、顶帽、黑帽等。我们需要知道形态学的高级形态，往往都是建立在复试和膨胀这两个基本操作之上的。

4.1 开运算

开运算(Opening Operation)，其实就是先腐蚀后膨胀的过程。
dst=open(src,element)=dilate(erode(src,element))
开运算可以用来消除小物体，在纤细点处分离物体，并且在平滑较边界的同时不明显改变其面积。
例如，请看下面的例子。左边的图像是原始图像，右边的图像是应用开运算后的结果。我们可以观察到，小圆点已经消失了。

4.2 闭运算

先膨胀后腐蚀的过程成为闭运算(Closing Operation)
dst=close(src,element)=erode(dilate(src,element)
闭运算能够排除小型黑洞(黑色区域)。

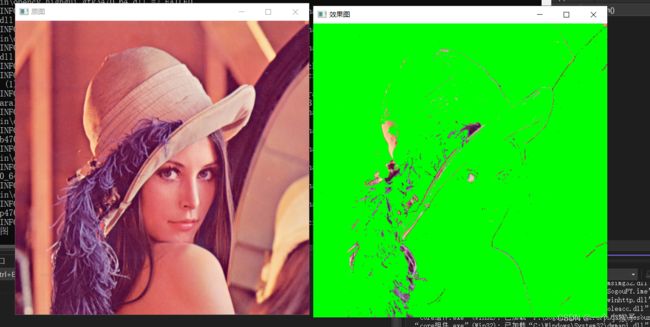
4.3 形态学梯度

形态学梯度(Morphological Gradient)是膨胀图与腐蚀图之差。
dst=morph-grad(src,element)=dialate(src,element)-erode(src,element)
它对寻找图像的轮廓很有用。

4.4 顶帽

顶帽运算(Top Hat)又常常被译为"礼帽"运算，是源图像与开运算之差。
dst=tophat(src,element)=src-open(src,element)
因为开运算带来的结果是放大了裂缝或者局部低亮度的区域。因此，从原图中减去开运算后的图，得到的效果突出了比原图轮廓周围的区域更明亮的区域，且这一操作与选择的核的大小相关。

顶帽运算往往用来分离比邻近点亮一些的斑点。在一幅图像具有大幅的背景，而微小物品比较有规律的情况下，可以使用顶帽运算进行背景提取。

4.5 黑帽

黑帽(Black Hat)运算是闭运算的结果图与原图像之差。
dst=blackhat(src,element)=close(src,element)-src
黑帽运算后的效果图突出了比原图轮廓周围的区域更暗的区域，且这一操作和选择的核的大小相关。所以黑猫运算用来分离比邻近点暗一些的斑块，效果图有着非常完美的轮廓。

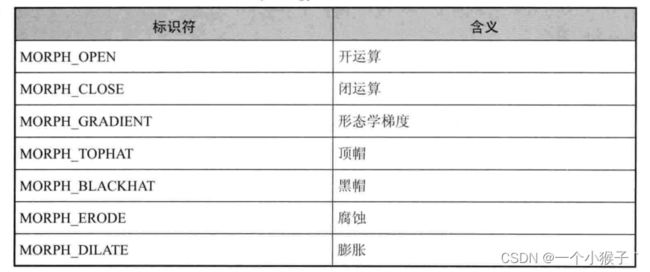
4.6 morphologyEx()函数

• 第一个参数：输入图像
• 第二个参数：输出图像
• 第三个参数：形态学操作的类型

  

• 第四个参数：核元素。它可以用getStructuringElement创建。
• 第五个参数：锚点与内核的位置。负值意味着锚点在内核中心。
• 第六个参数：应用函数的次数，默认值为1。

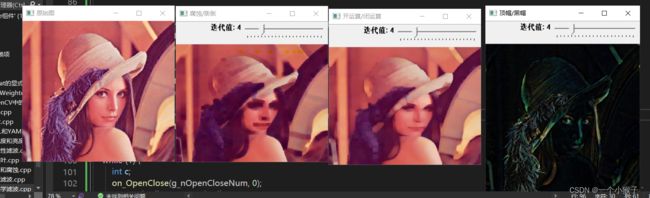
4.7 综合案例：形态学滤波

#include
using namespace std;
using namespace cv;

Mat g_srcImage, g_dstImage;
int g_nElementShape = MORPH_RECT;//元素结构的形状

//TrackBar参数
int g_nMaxIterationNum = 10;
int g_nOpenCloseNum = 0;
int g_nErodeDilateNum = 0;
int g_nTopBlackHatNum = 0;

// 开运算/闭运算窗口的回调函数
static void on_OpenClose(int, void*) {
	//偏移量的定义
	int offset = g_nOpenCloseNum - g_nMaxIterationNum;//偏移量
	int Absolute_offset = offset > 0 ? offset : -offset;

	//核
	Mat element = getStructuringElement(g_nElementShape,
		Size(Absolute_offset * 2 + 1, Absolute_offset * 2 + 1),
		Point(Absolute_offset, Absolute_offset));
	
	if (offset < 0)
		morphologyEx(g_srcImage, g_dstImage, MORPH_OPEN, element);
	else
		morphologyEx(g_srcImage, g_dstImage, MORPH_CLOSE, element);

	imshow("开运算/闭运算", g_dstImage);
}

// 腐蚀/膨胀窗口的回调函数
static void on_ErodeDilate(int, void*) {
	//偏移量的定义
	int offset = g_nErodeDilateNum - g_nMaxIterationNum;//偏移量
	int Absolute_offset = offset > 0 ? offset : -offset;

	//核
	Mat element = getStructuringElement(g_nElementShape,
		Size(Absolute_offset * 2 + 1, Absolute_offset * 2 + 1),
		Point(Absolute_offset, Absolute_offset));

	if (offset < 0)
		morphologyEx(g_srcImage, g_dstImage, MORPH_ERODE, element);
	else
		morphologyEx(g_srcImage, g_dstImage, MORPH_DILATE, element);

	imshow("腐蚀/膨胀", g_dstImage);
}

// 顶帽/黑帽窗口的回调函数
static void on_TopBlackHat(int, void*) {
	//偏移量的定义
	int offset = g_nErodeDilateNum - g_nMaxIterationNum;//偏移量
	int Absolute_offset = offset > 0 ? offset : -offset;

	//核
	Mat element = getStructuringElement(g_nElementShape,
		Size(Absolute_offset * 2 + 1, Absolute_offset * 2 + 1),
		Point(Absolute_offset, Absolute_offset));

	if (offset < 0)
		morphologyEx(g_srcImage, g_dstImage, MORPH_TOPHAT, element);
	else
		morphologyEx(g_srcImage, g_dstImage, MORPH_BLACKHAT, element);

	imshow("顶帽/黑帽", g_dstImage);
}



int main() {
	g_srcImage = imread("../../image/1.tif");
	namedWindow("原始图",0);
	imshow("原始图", g_srcImage);

	namedWindow("开运算/闭运算",0);
	namedWindow("腐蚀/膨胀", 0);
	namedWindow("顶帽/黑帽", 0);

	//参数赋值
	g_nOpenCloseNum = 9;
	g_nErodeDilateNum = 9;
	g_nTopBlackHatNum = 2;

	//分别为三个窗口创建滚动条
	createTrackbar("迭代值", "开运算/闭运算", &g_nOpenCloseNum,
		2 * g_nMaxIterationNum + 1, on_OpenClose);
	on_OpenClose(g_nOpenCloseNum, 0);

	createTrackbar("迭代值", "腐蚀/膨胀", &g_nErodeDilateNum,
		2 * g_nMaxIterationNum + 1, on_ErodeDilate);
	on_OpenClose(g_nOpenCloseNum, 0);

	createTrackbar("迭代值", "顶帽/黑帽", &g_nTopBlackHatNum,
		2 * g_nMaxIterationNum + 1, on_TopBlackHat);
	

	while (1) {
		int c;
		on_OpenClose(g_nOpenCloseNum, 0);
		on_ErodeDilate(g_nErodeDilateNum, 0);
		on_TopBlackHat(g_nTopBlackHatNum, 0);
		c = waitKey(0);//获取按键

		//按下q或者esc程序退出
		if ((char)c == 'q', (char)c == 27)
			break;
		if ((char)c == 49) //1的ASCII码
			g_nElementShape = MORPH_ELLIPSE;
		else if ((char)c == 50)
			g_nElementShape = MORPH_RECT;
		else if ((char)c == 51)
			g_nElementShape = MORPH_CROSS;

		else if ((char)c == ' ')
			g_nElementShape = (g_nElementShape + 1) % 3;
	}
	return 0;
}

5.漫水填充

漫水填充是一种用特定的颜色填充连通区域，通过设置可连通像素的上下限以及连同方式， 来达到不同的填充效果的方法。漫水填充经常被用来标记或分离图像的一部分，以便其进行进一步处理或分析，也可以用来从输入图像获取掩码区域，掩码会加速处理的过程，或只处理掩码指定的像素点，操作的结果总是某个连续的区域。

5.1 漫水填充：floodFill函数

第一个版本的floodFill():带有掩膜mask

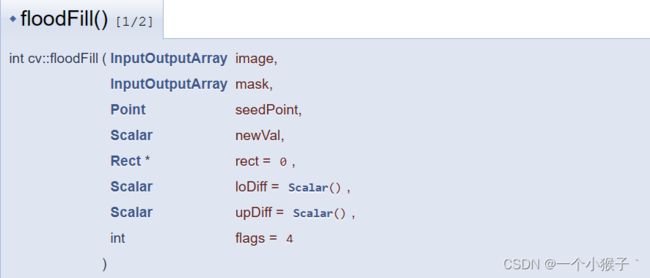
第一个版本的floodFill():不带掩膜mask

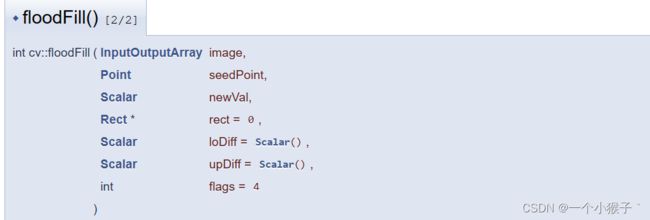
• 第一个参数：输入/输出1或3通道、8位或浮点图像。
• 第二个参数：操作掩码，应该是一个单通道的8位图像，比图像宽2像素，高2像素。如果传递了一个空的Mat，它将被自动创建。由于这既是一个输入参数又是一个输出参数，你必须负责初始化它。填充不能跨越输入掩码中的非零像素。例如，一个边缘检测器的输出可以作为一个掩码，在边缘停止填充。在输出时，掩码中与图像中的填充像素相对应的像素被设置为1或如下所述的标志中的指定值。此外，该函数用1填充蒙版的边界，以简化内部处理。因此，可以在多次调用该函数时使用同一个掩码，以确保填充的区域不重叠。
• 第三个参数：漫水填充算法的起始点。
• 第四个参数：像素点被染色的值，即在重绘区域像素的新值。
• 第五个参数：用于设置floodFill函数将要重绘区域的最小边界矩形区域。
• 第六个参数：Scalar类型的loDiff，有默认值Scalar()，表示当前观察像素值与其部件邻域像素值或者待加入该部件的种子像素之间的亮度或颜色之负差的最大值。
• 第七个参数：upDiff，有默认值Scalar()，表示当前观察像素值与其部件邻域像素值或者待加入该部件的种子像素之间的亮度或颜色之正差的最大值。
• 第八个参数：操作标志。前8位包含一个连接值。默认值为4意味着只考虑四个最近的邻居像素（那些共享一个边缘的像素）。连通性值为8意味着八个最近的邻居像素（那些共享一个角的像素）将被考虑。接下来的8位（8-16）包含一个1到255之间的值，用来填充掩码（默认值是1）。例如，4 | ( 255 << 8 ) 将考虑4个最近的邻居，并以255的值填充遮罩。下面的附加选项占据了更高的位数，因此可以使用位数或（|）与连接性和掩码填充值进一步结合。

#include
using namespace std;
using namespace cv;

int main() {
	Mat src = imread("../../image/1.tif");
	imshow("原图", src);
	Rect ccomp;
	floodFill(src, Point(250, 250), Scalar(0, 255, 0), &ccomp,
		Scalar(20, 20, 20), Scalar(20, 20, 20));
	imshow("效果图", src);
	waitKey();
	return 0;
}

6.图像金字塔与图片尺寸缩放

6.1 引言

我们经常会蒋某中尺寸的图像转换成其他尺寸的图像，如果要放大或者缩小图片的尺寸，可以用OpenCV提供的如下两种方法。

• resize函数。这是最直接的方式。
• pyrUp()、PyrDown()函数。即图像金字塔相关的两个函数，对图像进行向上采样和向下采样的操作。

6.2 关于图像金字塔

图像金字塔是图像中多尺度表达的一种，最主要用于图像的分割，是一种以多分辨率来解释图像的有效但概念简单的结构。
图像金字塔最初用于机器视觉和图像压缩，一幅图像的金字塔是一系列以金字塔形状排列的，分辨率逐步降低且来源于同一张原始图片的几何。其通过梯次向下采样获得，直到达到某个终止条件才停止采样。
金字塔的底部是待处理图像的高分辨率表示，而顶部是低分辨率的近似。我们将一层一层的图像比喻成金字塔，层级越高，则图像越小，分辨率越低。

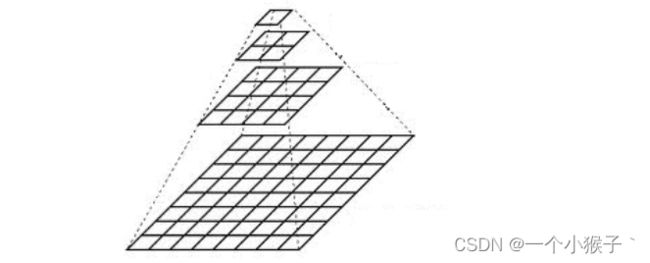
一般有两种类型的图像金字塔出现在文献以及实际应用中。

• 高斯金字塔——用来向下采样，主要的图像金字塔

• 拉普拉斯金字塔——用来从金字塔底层图像重建上层未采样的图像，在数字图像处理中也即是预测残差，可以对图像进行最大程度的还原，配合高斯金字塔一起使用。
  要从金字塔第i层生成第i+1层(从下往上，第i+1层表示为G_i+1)，我们先要用高斯核对G_i进行卷积，然后删除所有偶数行和偶数列，新得到图像面积会变成源图像的四分之一。按上诉过程对输入图像G₀执行操作就可产生出整个金字塔。

• 对图像向上采样——pyrUp函数

• 对图像向下采样——pyrDown函数
  这里的向下和向上采样，是针对图像的尺寸而言的(和金字塔的方向相反)，向上就是图像尺寸加倍，向下就是尺寸减半。
  但需要注意的是，pryUp和pryDown不是互逆的操作，即pryUp不是降采样的逆操作。这种情况下，图像首先在每个维度上扩大为原来的两倍，新增的行(偶数行)以0填充。然后给指定的滤波器进行卷积(实际上是一个在每个维度都扩大为原来两倍的过滤器)去估计“丢失”像素的近似值。
  pryDown()是一个会丢新信息的函数。为了恢复原来更高的分辨率的图像，我们要获得由降采样操作丢失的信息，这些数据就和拉普拉斯金字塔有关了。

6.3 高斯金字塔

高斯金字塔是通过高斯平滑和亚采样获得一系列下采样图像，也就是说第K层高斯金字塔通过平滑 、亚采样就能获得K+1层高斯图像。高斯金字塔包含了一系列低通滤波器，期截止频率从上一层到下一层以因子2逐渐增加，所以高斯金字塔可以跨越很大的频率范围。
1.对图像的向下采样
为了获取层级为G_i+1的金字塔图像，我们采用如下方法：
1）对图像G_i进行高斯内核卷积
2）将所有偶数行和列去除
得到的图像即为G_i+1的图像。显而易见，结果图像只有原图像的四分之一。通过对输入图像G_i不停迭代以上步骤就会得到整个金字塔。同时我们也可以看到，向下取样会逐渐丢失图像的信息。

2.对图像的向上采样
如果想放大图像,则需要通过向上采样操作得到,具体方法如下。
1）将图像在每个方向扩大为原来的两倍，新增的行和列以0填充
2）使用先前同样的内核(乘以4)与放大后的图像卷积，获得"新增像素"的近似值。
得到的图像即为放大后的图像，但是与原来的图像相比会发觉比较模糊，因为在缩放的过程中已经丢失了一些信息。如果想在缩小和放大整个过程这能够减少信息的丢失，这些数据就形成了拉普拉斯金字塔。

6.4 拉普拉斯金字塔

关于图像金字塔非常重要的一个应用就是图像分割。图像分割的话，先要建立一个图像金字塔，然后对G_i和G_i+1的直接依照对应的关系，建立起"父与子"关系。而快速初始化分割可以现在金字塔高层的低分辨率上完成，然后逐层对分割加以优化。

6.5 图像金字塔相关API函数

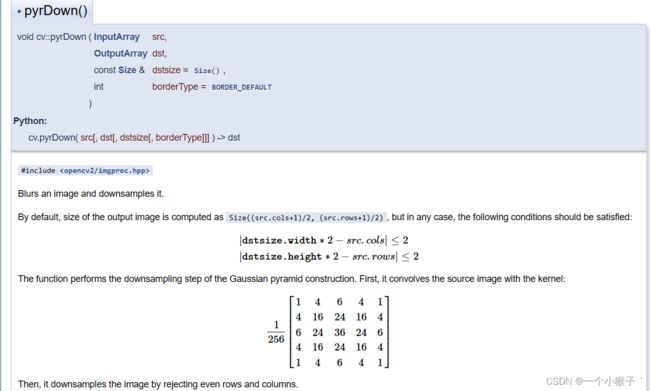
1.向上采样pyrUp()函数
pyrUp()函数的作用是向上采样并模糊一张图像，说白了就是放大一张图片。
void pyrUp(InputArray src,OutputArray dst,const Size& dstsize=Size(),int borderType=BORDER_DEFAULT)

• 第一个参数：InputArray类型的src，输入图像，即源图像
• 第二个参数：输出图像
• 第三个参数：const Size&类型的dstsize，输出图像的大小；有默认值Size()，即默认情况下，由Size(src.cols2,src.rows2)来进行计算。

#include
using namespace std;
using namespace cv;

int main() {
	Mat srcImage = imread("../../image/lena_color_256.tif");
	Mat tmpImage, dstImage;
	tmpImage = srcImage;

	imshow("原图", srcImage);
	
	pyrUp(tmpImage, dstImage, Size(tmpImage.cols * 2, tmpImage.rows * 2));

	imshow("效果图", dstImage);
	waitKey();
	return 0;
}

2.向下采样pyrDown()函数

#include
using namespace std;
using namespace cv;

int main() {
	Mat srcImage = imread("../../image/lena_color_256.tif");
	Mat tmpImage, dstImage;
	tmpImage = srcImage;

	imshow("原图", srcImage);
	
	pyrDown(tmpImage, dstImage, Size(tmpImage.cols / 2, tmpImage.rows / 2));

	imshow("效果图", dstImage);
	waitKey();
	return 0;

}

6.6 尺寸调整：resize()函数

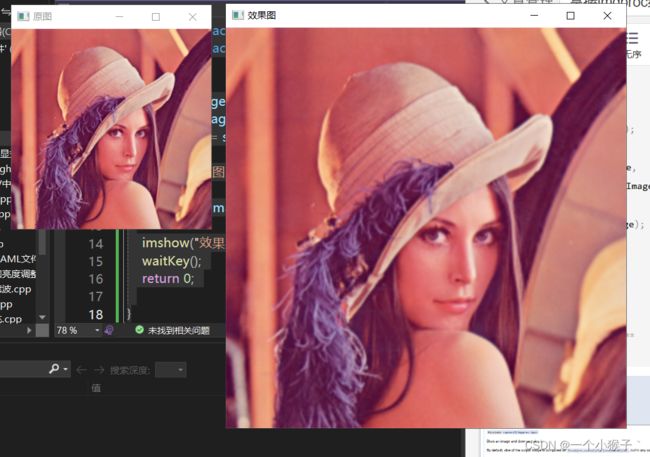
resize()函数将源图像精确地转换为指定尺寸的目标图像。如果原图像中设置了ROI，那么resize()函数会对原图像的ROI区域进行调整图像尺寸的操作，来输出到目标图像中。若目标图像中已经设置了ROI区域，不难理解resize()将会对源图像进行尺寸调整并填充到目标图像的ROI中。
很多时候，我们并不用考虑第二个参数dst的初始图像和尺寸(即直接定义一个Mat类型，不用对其初始化)，因为其尺寸和类型可以由src，dsize、fx和fy这几个参数确定
void resize(InputArray src, OutputArray dst, Size dsize, double fx=0, double fy=0, int interpolation=INTER_LINEAR)

• 第一个参数：InputArray类型的src，输入图像，即源图像，填Mat类的对象即可。
• 第二个参数：输出图像；它的大小为dsize（当它不为零时）或由src.size()、fx和fy计算出的大小；dst的类型与src的类型相同。
• 第三个参数：输出图像的大小。如果它为0时，计算公式如下：

  $dsize=Size(round(fx\ast src.cols),round(fy\ast src.rows))$

• 第四个参数：沿着水平轴的缩放系数；当它等于0时，它被计算为

  $(double)dsize.width/src.cols$

• 第五个参数：沿纵轴的缩放系数；当它等于0时，它被计算为

  $(double)dsize.height/src.rows$

resize的调用范例：
方式一：

Mat dstImage = Mat::zeros(512,512,CV_8UC3);
Mat srcImage=imread("../../image/1.tif");
//显示指定dsize=dstImage.size()，那么fx和fy会被计算出来，不用额外指定
resize(srcImage,dstImage,dstImage.size());

方式二：

Mat dstImage;
Mat srcImage=imread("../../1.tif");
//指定fx和fy，让函数计算出目标图像的大小
resize(srcImage,dstImage,Size(),0.5,0.5);

resize函数案例

#include
using namespace std;
using namespace cv;

int main() {
	Mat srcImage = imread("../../image/lena_color_256.tif");
	Mat tmpImage, dstImage1, dstImage2;
	tmpImage = srcImage;
	imshow("原始图", srcImage);

	resize(tmpImage, dstImage1, Size(tmpImage.cols / 2, tmpImage.rows / 2),
		(0, 0), (0, 0), 3);

	resize(tmpImage, dstImage2, Size(tmpImage.cols * 2, tmpImage.rows * 2),
		(0, 0), (0, 0), 3);

	imshow("缩小", dstImage1);
	imshow("放大", dstImage2);

	waitKey();
	return 0;
}

7 阈值化

在对各种图形进行处理操作的工程中，我们常常需要对图像中的像素做出取舍与决策，直接提出一些低于或高于一定值的像素。
阈值可以被视作最简单的图像分割方法。比如，从一幅图像中利用阈值分割出我们需要的物体部分。这样的图像分割方法基于图像中物体与背景之间的灰度差异，而且此分割属于像素级的分割。为了从一幅图像中提取我们需要的部分，用该用图像中的每一个像素点的灰度值与选取的阈值进行比较，并作出相应的判断。注意:阈值的选取依赖于具体的问题。即物体在不同的图像中有可能会有不同的灰度值。
一旦找到了需要分割的物体的像素点，可以对这些像素点设定一些特定的值来表示。例如，可以将该物体的像素点的灰度值设置为0(黑色)，其他的像素点灰度值为255(白色)。当然像素点的灰度值可以任意，但最好设定的两种颜色对比度较强，以方便观察结果。

7.1 固定阈值操作：Threshold()

函数Threshold()对单通道数组应用固定阈值操作。该函数的典型应用是对灰度图像进行阈值操作得到二值图像(compare()函数也可以达到此目的)或者是去掉噪声，例如过滤很小或很大像素值的图像点。
double threshold(InputArray src,OutputArray dst,double thresh,double maxval,int type)

• 第一个参数： 输入图像（多通道，8位或32位浮点）。
• 第二个参数：与src相同大小和类型、相同通道数的输出阵列。
• 第三个参数：阈值
• 第四个参数：与 THRESH_BINARY 和 THRESH_BINARY_INV 阈值类型一起使用的最大值。
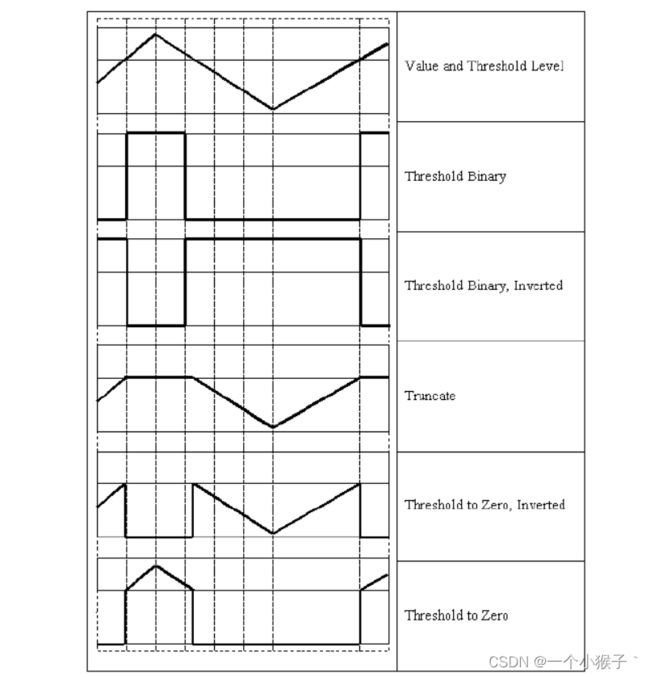
• 第五个参数：阈值类型

  
  

7.2 自适应阈值操作：adaptiveThreshold()函数

void adaptiveThreshold ( InputArray src, OutputArray dst, double maxValue, int adaptiveMethod, int thresholdType, int blockSize, double C )

• 第一个参数：输入图像
• 第二个参数：输出图像
• 第三个参数：给像素赋的满足条件的非零值
• 第四个参数：用于指定要使用的自适应阈值算法，可取值为ADAPTIVE_THRESH_MEAN_C或ADAPTIVE_THRESH_GAUSSIAN_C。
• 第五个参数：阈值类型，取值必须为THRESH_BINARY、THRESH_BINARY_INV其中之
• 第六个参数：int类型的blockSize，用于计算阈值大小的一个像素的邻域尺寸，取值为3，5，7等。
• 第七个参数：double类型的C，减去平均或加权平均值后的常数值。

7.3 阈值操作综合案例

#include
using namespace std;
using namespace cv;

#define WINDOW_NAME "程序窗口"

int g_nThreshouldValue = 100;
int g_nThreshouldType = 3;
Mat g_srcImage, g_grayImage, g_dstImage;


void on_Threshold(int, void*) {
	threshold(g_grayImage, g_dstImage, g_nThreshouldValue,
		255, g_nThreshouldType);

	imshow(WINDOW_NAME, g_dstImage);
}

int main() {
	g_srcImage = imread("../../image/1.tif");
	if (!g_srcImage.data) {
		cout << "读取图片失败" << endl;
		return false;
	}

	cvtColor(g_srcImage, g_grayImage, COLOR_RGB2GRAY);
	imshow("原图", g_grayImage);
	namedWindow(WINDOW_NAME);

	createTrackbar("模式", WINDOW_NAME, &g_nThreshouldType,
		4, on_Threshold);

	createTrackbar("参数值", WINDOW_NAME, &g_nThreshouldValue,
		255, on_Threshold);

	on_Threshold(0, 0);

	while (1) {
		int key;
		key = waitKey(20);
		if ((char)key == 27)
			break;
	}
}