LCS（最大公共子序列）问题

1. LCS是个啥？

LCS，即最大公共子序列。
与最长公共子串不同，最大公共子序列只要求有相同的元素，且顺序相同，但不要求连续。

如：
X=B,C,B,D,A,B>
Y=<B,D,C,A,B,A>
则LCS=Z=

2. LCS相关分析与算法

（1） Xi 为字符串X的i前缀，Yj为字符串的j前缀
（2）若X_m=Y_n,则Z_k=X_m=Y_n,LCS(X_m,Y_n)=LCS(X_m-1,Y_n-1)+X_m
（3）若X_n!=Y_n,要么LCS(X_m,Y_n)=LCS(X_m,Y_n-1),要么LCS(X_m-1,Y_n)

即LCS(X_m,Y_n)=max{LCS(X_m,Y_n-1), LCS(X_m-1,Y_n)}

显然，需要使用动态规划

使用长度数组，根据上述分析可得
用二维数组C(i,j)记录Xi与Yi的最大公共子序列长度

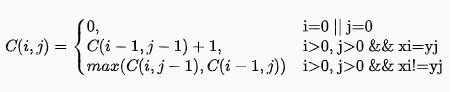
用二维数组b(i,j)记录C(i,j)的值是由那个子问题解决达到的
即C(i,j)是由C(i-1, j-1), C(i, j-1)或C(i-1, j)得到的

例如：

b(i,j)记录的是所谓的方向：up, left, left-up

通过上述分析可得：
C(m,n)的大小为LCS的长度
通过b(i,j)的回溯可得LCS的内容，即子串

3. 代码实现

C(i, j)的实现

for (int i = 0; i <= size1; i++)
	{
		for (int j = 0; j <= size2; j++)
		{
			if (str1[i] == str2[j]) 
			{
				c[i][j] = c[i - 1][j - 1] + 1;
				b[i][j] = leftup;
			}
			else if (str1[i] != str2[j]) {
				if (c[i - 1][j] >= c[i][j - 1])
				{
					c[i][j] = c[i - 1][j];
					b[i][j] = up;
				}
				if (c[i - 1][j] < c[i][j - 1])
				{
					c[i][j] = c[i][j - 1];
					b[i][j] = Left;
				}
				
			}
		}
	}

回溯算法：

void printit(int **direction, int row, int col,int length1, int length2,char* str1, char* str2)   //打印LCS
{
	if (!(row < length1 && col < length2))
		return;
	if (direction[row][col] == leftup)
	{
		if (row > 0 && col > 0)
			printit(direction, row - 1, col - 1, length1, length2,str1,str2);
			cout << str1[row];
	}
	if (direction[row][col] == Left)
	{
		printit(direction, row, col - 1, length1, length2, str1, str2);
	}
	if (direction[row][col]==up)
		printit(direction, row - 1, col, length1, length2, str1, str2);
}

完整代码

#include 
#include 
#include 
#include 
using namespace std;
int c[150][150], **b;          //C为长度数组，b为方向数组
char str1[100], str2[100];
char str[100];
int up = 1;
int Left = 2;
int leftup = 3;

void printit(int **direction, int row, int col,int length1, int length2,char* str1, char* str2)   //打印LCS
{
	if (!(row < length1 && col < length2))
		return;
	if (direction[row][col] == leftup)
	{
		if (row > 0 && col > 0)
			printit(direction, row - 1, col - 1, length1, length2,str1,str2);
			cout << str1[row];
	}
	if (direction[row][col] == Left)
	{
		printit(direction, row, col - 1, length1, length2, str1, str2);
	}
	if (direction[row][col]==up)
		printit(direction, row - 1, col, length1, length2, str1, str2);
}


int main()
{
	string s1 = "ABCBDAB";
	string s2 = "BDCABA";
	int size1 = s1.length()-1;
	int size2 = s2.length()-1;
	strcpy_s(str1, s1.c_str());
	strcpy_s(str2, s2.c_str());
	b = (int**)(new int[150]);
	for (int i = 0; i < 150; i++)
		b[i] = (int*)(new int[150]);
	for (int i = 0; i <= size1; i++)
	{
		for (int j = 0; j <= size2; j++)
		{
			if (str1[i] == str2[j]) 
			{
				c[i][j] = c[i - 1][j - 1] + 1;
				b[i][j] = leftup;
			}
			else if (str1[i] != str2[j]) {
				if (c[i - 1][j] >= c[i][j - 1])
				{
					c[i][j] = c[i - 1][j];
					b[i][j] = up;
				}
				if (c[i - 1][j] < c[i][j - 1])
				{
					c[i][j] = c[i][j - 1];
					b[i][j] = Left;
				}
				
			}
		}
	}

	cout << "最长公共子序列为：" << " ";
	printit(b, size1, size2, size1+1, size2+1, str1, str2);
	cout << endl;
	cout << "长度为：" << " ";
	cout << c[size1][size2] << endl;

	return 0;
	
}

运行结果

第一次很有信心地更dp的算法。（第一次真正搞懂）
后面会继续更相关的题目与算法例子。