运动目标检测之光流法(4)LK金字塔论文翻译
金字塔型实现的Lucas Kanade特征跟踪器的算法描述
Jean-Yves Bouguet
Intel Corporation
Microprocessor Research Labs
[email protected]
1.问题说明
设I和J是两幅二维灰度图像。两个量I(x) = I(x,y)和J(x) = J(x,y)则是两个图像的灰度值,即位置x = [x,y]T,其中x和y是普通图像点x的两个像素坐标。图像I有时被称为第一图像,而图像J被称为第二图像。对于实际问题,图像I和J是离散函数(或数组),左上角像素坐标向量为[0 0]T,设nx和ny为两幅图像的宽度和高度。那么右下像素坐标向量就是[nx-1 ny-1]T。
假设第一幅图像I上的一个图像点u = [ux uy]T,特征跟踪的目标是找到第二幅图像J上的对应位置v = u + d = [ux + dx uy + dy]T,则称I(u)和J(v)“相似”。向量d = [dx dy]T是x处的图像速度,也称为x处的光流。由于孔径问题,有必要在二维邻域意义上定义相似性的概念。设ωx和ωy两个整数。我们将图像速度d定义为使残差函数ϵ最小化的向量,残差函数定义如下:
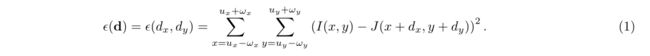
根据该定义,相似性函数是在大小为(2ωx + 1) (2ωy + 1)的图像邻域上测量的。这个邻域也将被称为集成窗口。ωx和ωy的典型值为2,3,4,5,6,7像素。
2 跟踪算法的描述
任何特征跟踪的两个关键要素是准确性和鲁棒性。精度分量涉及与跟踪相关的局部亚像素精度。直觉上,为了不“消除”图像中包含的细节(即,小的ωx和ωy值),小的积分窗口将是优选的。这在图像中两个斑块可能以非常不同的速度移动的遮挡区域尤其需要。
鲁棒性分量涉及跟踪相对于光照变化的灵敏度、图像运动的大小,…特别地,为了处理大的运动,选择大的积分窗口显然是更可取的。事实上,仅考虑等式1,最好是dx<=ωx和dy<=ωy(除非有一些先验匹配信息)。因此,当选择积分窗口大小时,在局部精度和鲁棒性之间有一个自然的折衷。为了提供该问题解决方案,我们提出了经典Lucas-Kanade算法的金字塔实现。Lucas-Kanade光流计算的迭代实现提供了足够的局部跟踪精度。
2.1 图像金字塔表示
定义大小为nx * ny的图像I的金字塔表示。设I0 = I为第0级图像。该图像本质上是最高分辨率的图像(原始图像)。该层图像的宽度和高度定义为n0x = nx和n0y = ny。然后以递归的方式构建金字塔表示:从I0计算I1,然后从I1计算I2,等等……设L = 1,2,…为一般的金字塔层,设IL - 1为L - 1层的像。nL−1x、nL−1y分别为IL−1的宽、高。图像IL−1的定义如下:

为了简化表示法,让我们定义图像IL−1周围一个像素的虚拟图像值(对于0≤x≤nL−1x−1和0≤y≤nL−1y−1):
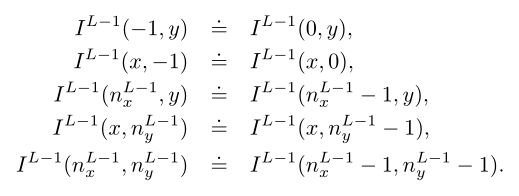
则方程2仅定义x、y的值为0≤2x≤nL−1x−1,0≤2y≤nL−1y−1。因此,IL的宽度nLx和高度nLy是满足以下两个条件的最大整数:

利用等式(2)、(3)、(4)递归地构建两个图像I和I的金字塔。Lm值是金字塔的高度(启发式选取)。 Lm的值是2,3,4。对于典型的图像大小,超过4级是没有意义的。例如,对于尺寸为640×480的图像I,图像I1、I2、I3和I4分别具有320×240、160×120、80×60和40×30的尺寸。超越四级在大多数情况下没有太大意义。金字塔表示背后的主要动机是能够处理大像素运动(大于积分窗口尺寸ωx和ωy)。因此,金字塔高度(Lm)也应该根据图像中的最大预期光流来适当选取。下一节详细描述跟踪操作,让我们更好地理解这个概念。最后观察: 图像分采样前,使用低通滤波器[1/4 / 1/4]×[1/4 / 1/4]T进行图像抗混叠。然而,在实践中(在C代码中),更大的抗混叠滤波器内核被用于金字塔构造[1/16 1/4 3/8 1/4 1/16] ×[1/16 1/4 3/8 1/4 1/16]T。
2.2金字塔特征跟踪
回想一下特征跟踪的目标:对于图像I中的给定点u,在图像J中找到其对应的位置v = u + d,或者找到其像素位移向量d(见等式1)。对于L = 0,…,Lm,定义uL = [uLx uLy],即金字塔图像IL上u点的相应坐标。根据我们对金字塔表示方程(2)、(3)和(4)的定义,向量uL计算如下:

方程5中的除法运算分别应用于两个坐标(在随后的方程中出现的乘法运算也是如此)。注意,u0 = u。
整个金字塔跟踪算法如下进行:首先,在金字塔的最深处Lm处计算光流;然后,该计算的结果以像素位移的初始猜测的形式传播到上级Lm-1(在Lm-1级);给定初始猜测,在Lm-1级计算精确的光流,并将结果传播到Lm-2级;以此类推,直到L0级(原始图像)。
现在让我们用更数学的细节来描述两个泛型级别L + 1和L之间的递归操作。假设从L层到L + 1层的计算可以初步猜测L层的光流gL = [gLx gLy]T然后,为了计算L的光流,需要找到使新的图像匹配误差函数最小化的剩余像素位移向量dL = [dLx dLy]T:

观察到,对于L的所有值,积分窗口具有恒定的大小(2ωx + 1) (2ωy + 1)。注意,初始猜测流向量gL用于预转换第二图像J中的图像补片。这样,残差流矢量dL = [dLx dLy]T很小,因此很容易通过标准的Lucas Kanade步骤来计算。
剩余光流dL的计算细节将在下一节2.3中描述。现在,让我们假设这个向量是计算出来的(以结束算法的主循环)。然后,通过传递表达式的新初始猜测gL-1,将计算结果传播到下一级L-1:

然后,通过相同的过程计算下一级光流剩余向量dL-1。通过光流计算(在第2.3节中描述)计算的这个向量的最小化函数ϵL−1(dL−1(等式6)。这个过程一直持续到达到最佳图像分辨率(L = 0)。该算法通过将Lm级的初始猜测值设置为零来初始化(在金字塔的最深层没有初始猜测值):

在最精细的光流计算之后,最终的光流解d(参考等式1)是可用的:

请注意,此解决方案可以用以下扩展形式表示:

金字塔实现的明显优势在于,在计算较大的整体像素位移向量d时,每个剩余光流向量dL可以保持非常小。假设每个基本光流计算步骤可以处理高达dmax的像素运动,则金字塔实现可以处理的整体像素运动变成dmax final = (2Lm+1-1) *dmax。例如,对于Lm = 3的金字塔深度,这意味着最大像素位移增益为15!这允许大的像素运动,同时保持积分窗口的尺寸相对较小。
2.3 迭代光流计算(迭代卢卡斯-卡纳德)
现在让我们描述核心光流计算。在金字塔的每一层L上,目标是找到使等式6中定义的匹配函数ϵL最小的向量dL。由于对所有级别L都执行相同类型的操作,现在让我们去掉上标L,并将新图像A和B定义如下:
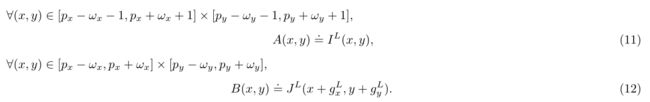
观察到A(x,y)和B(x,y)的定义域略有不同。事实上,A(x,y)是在大小为(2ωx + 3)*(2ωy + 3)的窗口上,而不是(2ωx + 1) (2ωy + 1)的窗口上定义的。当使用中心差分算子(方程)计算A(x,y)的空间导数时,这种差异将变得明显。(见19和20)。为了清楚起见,让我们改变位移向量的名称ν = [νx νy]T = dL,以及图像位置向量p = [px py]T = uL。按照新的符号,目标是找到使匹配函数最小化的位移向量ν = [νx νy]T:
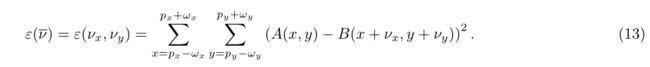
标准的迭代Lucas-Kanade可以应用于该任务。在最优时,ε对ν的一阶导数为零

对导数展开可得:
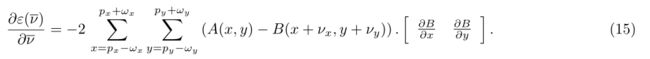
现在让我们用B(x + νx,y + νy)关于点ν = [0 0]T的一阶泰勒展开式来代替它(由于金字塔方案,这很有可能是有效的近似,因为我们期望一个小的位移向量):
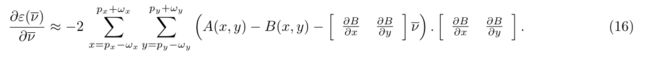
注意到,A(x, y)−B(x, y)可以解释为在点[x y]T上的时间图像导数:∀(x, y)∈[px−ωx, px + ωx] × [py−ωy, py + ωy],


观察到图像导数Ix和Iy可以从点p的(2ωx + 1) (2ωy + 1)邻域中的第一图像A(x,y)直接计算,而与第二图像B(x,y)无关(这种观察的重要性将在稍后描述流动计算的迭代版本时变得明显)。如果对导数使用中心差分算子,则两个导数像有如下表达式:
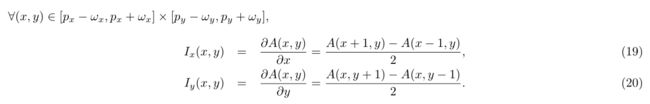
在实践中,Sharr算子用于计算图像导数(非常类似于中心差分算子)。根据这个新的表示法,式16可以写成:
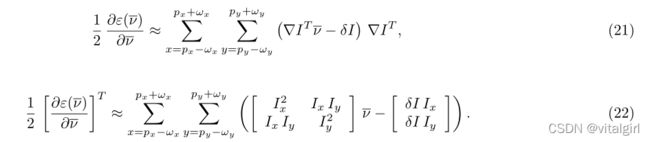
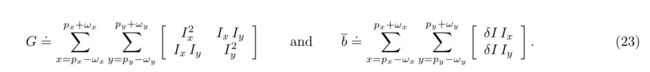
则式22可写成:

因此,由式14可知,最优光流矢量为

只有当矩阵G可逆时,这个表达式才有效。这相当于说图像A(x,y)在点p的邻域中包含x和y方向上的梯度信息。
这是标准的Lucas-Kanade光流方程,只有当像素位移很小时才有效(为了验证一阶泰勒展开)。在实践中,为了得到一个准确的解决方案,有必要对这个方案进行多次迭代(以牛顿-拉夫森的方式)。
既然我们已经介绍了数学背景,让我们给出算法的迭代版本的细节。这一块略,有意向可以去原论文查看。
2.4 金字塔跟踪算法综述
现在让我们用伪代码的形式来总结整个跟踪算法。在正文中找到方程的详细信息(特别是定义领域)。


2.5 亚像素计算
将所有计算保持在亚像素精度水平是绝对必要的。因此,有必要能够计算整数像素之间的位置处的图像亮度值(例如参考等式11、12和26)。为了计算子像素位置的图像亮度,我们建议使用双线性插值。
设L是一般的金字塔等级。假设我们需要图像值IL(x,y ),其中x和y不是整数。设xo和yo是x和y的整数部分(比x和y小的较大整数)。设αx和αy是两个提醒值(在0和1之间),如:

然后,IL(x, y)可由原始图像亮度值通过双线性插值计算得到:
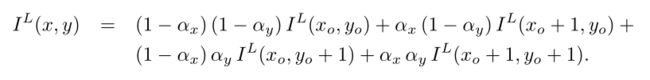
让我们做一些与亚像素计算相关的观察(重要的实现问题)。参考2.4节给出的算法总结。当计算邻域(x,y)∈[px-ωx,px+ωx][py-ωy,py + ωy]中的两个图像导数Ix(x,y)和Iy(x,y)时,需要邻域(x,y)∈[px-ωx-1,px+ωx+1][py-ωy-1,py + ωy + 1]中IL(x,y)的亮度值(参见19,20)。当然,中心点p = [px py]T的坐标不保证是整数。将pxo和pyo称为px和py的整数部分。那么我们可以写:

其中pxα和pyα是0到1之间的相关提醒值。因此,为了通过双线性插值计算邻域(x,y)∈[px-ωx-1,px+ωx+1][py-ωy-1,py + ωy + 1]中的图像补片IL(x,y),有必要使用整数网格补片(x,y)∈[pxo-ωx-1,pxo+ωx+2][ pyo-ωy-1,pyo + ωy + 1]中的原始亮度值IL(x,y)(回忆一下,ωx和ωy都是整数)。
计算邻域(x,y)∈[px-ωx,px+ωx][py-ωy,py + ωy]中的像差δIk(x,y)时也会出现类似情况(参见第2.4节)。事实上,为了计算δIk(x,y),需要有所有(x,y)∈[px-ωx,px+ωx][py-ωy,py + ωy]的值J。……这段公式太多,见原文如下

2.6 跟踪靠近图像边界的特征
非常有用的观察是,可以处理足够靠近图像边界的点,使它们的积分窗口的一部分在图像之外。当金字塔等级Lm的数量很大时,这个观察变得非常重要。事实上,如果我们总是强制(2ωx + 1) (2ωy + 1)窗口在图像内以便被跟踪,那么在图像IL周围都存在宽度为ωx(和ωy)的“禁带”。如果Lm是金字塔的高度,这意味着原始图像I周围的有效禁带宽度为2Lm ωx(和2Lm ωy)。对于较小的ωx、ωy和Lm值,这可能不会构成明显的限制,但是,对于较大的积分窗口尺寸,更重要的是对于较大的Lm值,这可能会变得非常麻烦。有些数字:ωx = ωy = 5个像素,Lm = 3导致图像周围有40个像素的禁带!
为了防止这种情况发生,我们建议保持跟踪积分窗口部分落在图像之外的点(在任何金字塔等级)。在这种情况下,除了出现在所有表达式中的求和(参见2.4节的伪代码)应该只在图像邻域的有效部分上进行之外,跟踪过程是相同的,即具有Ix(x,y),Iy(x,y)和δIk(x,y)的有效条目的邻域部分 (参见第2.4节)。请注意,在执行Lucas-Kanade迭代循环(遍历伪代码中的索引k—第2.4节)时,有效的求和区域可能会有所不同。事实上,在一次次迭代中,图像差值δIk(x, y)的有效条目可能会随着平移矢量[gLx + νk−1x gLy + νk−1y]T的变化而变化。此外,注意当计算失配向量bk和梯度矩阵G时,求和区域必须相同(为了数学保持有效)。因此,在这种情况下,G矩阵必须在每次迭代时在循环内重新计算。然而,差分patch Ix(x, y)和Iy(x, y)可以在迭代循环之前计算一次。
当然,如果点p = (px py) T(社区中心)超出图像,或者相应的跟踪点(px x + gLx +νk−1 py + g + yνk−1)超出图像的J L,它是合理的申报“失落的”,而不是追求跟踪。
2.7 宣布一个特征“丢失”
有两种情况会导致“丢失”特征。第一种情况非常直观:点落在图像之外。我们已经在2.6节讨论了这个问题。丢失的另一种情况是当被跟踪点周围的图像片在图像I和图像J之间变化太大时(该点由于遮挡而消失)。请注意,要精确量化这一条件要困难得多。例如,如果特征点的最终成本函数(ϵ(d)大于阈值,则该特征点可以被声明为“丢失”(见等式1)。当决定一个阈值时,一个问题出现了。当在一个完整的序列中的许多图像上跟踪一个点时,它特别敏感。事实上,如果跟踪是基于连续的图像对进行的,则被跟踪的图像块(用作参考)在每个轨迹处被隐含地初始化。因此,即使两个连续图像之间的图像差异非常小,该点也可能在整个扩展序列中漂移。在处理长序列时,这个漂移问题是一个非常经典的问题。一种方法是跟踪序列中的特征点,同时保持特征块外观的固定参考(使用特征出现的第一幅图像)。遵循这一技巧,ϵ(d这个量就有了更多的含义。然而,当采用这种方法时,另一个问题出现了:一个特性可能会被过快地宣布“丢失”。我们设想回答该问题的一个方向是使用仿射图像匹配来确定丢失的轨迹(参见Shi和Tomasi在[1]中)。
迄今为止已知的最佳技术是将目前提出的传统跟踪方法(基于图像对)与仿射图像匹配(使用特征补片的唯一参考)相结合来计算匹配,以确定错误跟踪。Shi和Tomasi在[1]中提供了关于该技术的更多信息。我们认为,最终,这种方法应该用于拒绝。值得注意的是,对于2D跟踪本身,本报告中提出的标准跟踪方案比单独的仿射跟踪执行得更好(更准确)。原因是仿射跟踪需要估计非常大量的参数:6个而不是标准方案的2个。许多人都观察到了这一点(例如http://www.stanford.edu/ssorkin/cs223b/final.html)。因此,只有在主2D跟踪引擎之上构建可靠的拒绝方案时,才应考虑仿射跟踪。
3 特征选择
到目前为止,我们已经描述了负责跟随图像I上的点u到另一个图像j上的另一个位置v的跟踪过程。然而,我们还没有描述首先选择I上的点u的方法。这一步称为特征选择。一旦跟踪的数学基础被引出,处理特征选择的问题是非常直观的。实际上,跟踪的中心步骤是光流矢量ηk的计算(参见2.4节中算法的伪代码)。在那一步,要求G矩阵是可逆的,或者换句话说,G的最小特征值必须足够大(大于一个阈值)。这表征了“容易跟踪”的像素。
因此,选择过程如下:
- 计算图像I中每个像素处的G矩阵及其最小特征值λm
- 称λmax为λm在整个图像上的最大值。
- 保留λm值大于λmax百分比的图像像素。这个百分比可以是10%,也可以是5%。
- 从这些像素中,保留局部最大值。像素(如果一个像素的λm值大于其3 3邻域中任何其他像素的λm值,则保留该像素)。
- 保持这些像素的子集,使得任何像素对之间的最小距离大于给定的阈值距离(例如10或5个像素)。
在该过程之后,剩余的像素通常是“易于跟踪”的。它们是馈送给跟踪器的选定特征点。
如果跟踪引擎可以处理非常大量的点,则可以省略由强制像素之间的最小成对距离组成的算法的最后步骤。这完全取决于特征跟踪器的计算性能。
最后,重要的是观察到没有必要为特征选择采用非常大的积分窗口(为了计算G矩阵)。事实上,对于选择来说,3 3窗口是足够的ωx = ωx = 1,并且应该被使用。对于跟踪,该窗口大小(3 3)通常太小(参见第1节)。