第四课 递归、分治

第四课 递归、分治

lc78.子集–中等

题目描述

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10
• nums 中的所有元素 互不相同

代码展示

class Solution {
public:
    vector<int> t;            // 用于暂存当前子集
    vector<vector<int>> ans;  // 用于存储所有子集的答案

    // DFS 函数，cur 表示当前处理的元素索引，nums 表示原始数组
    void dfs(int cur, vector<int>& nums) {
        if (cur == nums.size()) {  // 如果当前索引等于数组大小，表示处理完了所有元素，将当前子集添加到答案中
            ans.push_back(t);
            return;
        }
        t.push_back(nums[cur]);    // 将当前元素加入子集
        dfs(cur + 1, nums);        // 递归处理下一个元素
        t.pop_back();              // 回溯，将当前元素从子集中移除
        dfs(cur + 1, nums);        // 继续递归处理下一个元素，不加入当前元素的情况
    }

    vector<vector<int>> subsets(vector<int>& nums) {
        dfs(0, nums);  // 从第一个元素开始递归生成子集
        return ans;    // 返回生成的所有子集
    }
};

lc77.组合–中等

题目描述

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

• 1 <= n <= 20
• 1 <= k <= n

代码展示

class Solution {
public:
    vector<int> temp;           // 用于暂存当前组合
    vector<vector<int>> ans;    // 用于存储所有组合的答案

    void dfs(int cur, int n, int k) {
        // 剪枝：如果当前已经选择的数字个数加上剩下的数字个数小于 k，就不可能构造出长度为 k 的组合，进行剪枝
        if (temp.size() + (n - cur + 1) < k) {
            return;
        }
        // 如果当前已经选择的数字个数等于 k，将当前组合加入答案中
        if (temp.size() == k) {
            ans.push_back(temp);
            return;
        }
        // 考虑选择当前位置的数字
        temp.push_back(cur);
        dfs(cur + 1, n, k);
        temp.pop_back();  // 回溯，将当前位置的数字移除，考虑不选择当前位置的数字
        dfs(cur + 1, n, k);
    }

    vector<vector<int>> combine(int n, int k) {
        dfs(1, n, k);  // 从第一个数字开始生成组合
        return ans;    // 返回生成的所有组合
    }
};

优化思路：

这个算法的改进之处在于：

1. 减少了递归的深度：在原来的算法中，即使不选择当前位置的数字，也会递归调用一次 dfs(cur + 1, n, k)，导致递归深度较大。改进后的算法只有在选择当前位置的数字时才会递归调用，减少了递归深度。
2. 减少了不必要的循环：原来的算法在循环时，遍历了所有可能的组合，包括不可能构成有效组合的情况。改进后的算法在循环时，通过限制 i 的取值范围，避免了生成无效组合的情况。

这个改进后的算法在性能上更优化，尤其是对于较大的输入，因为它减少了不必要的递归和循环操作。

class Solution {
public:
    vector<vector<int>> combine(int n, int k) {
        vector<vector<int>> result;
        vector<int> current;
        backtrack(result, current, n, k, 1);
        return result;
    }

private:
    void backtrack(vector<vector<int>>& result, vector<int>& current, int n, int k, int start) {
        if (k == 0) {
            result.push_back(current);
            return;
        }

        for (int i = start; i <= n - k + 1; ++i) { // 减去 k - 1 个数，保证剩余的数足够构成组合
            current.push_back(i);
            backtrack(result, current, n, k - 1, i + 1);
            current.pop_back();
        }
    }
};

lc46.全排列–中等

题目描述

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

• 1 <= nums.length <= 6
• -10 <= nums[i] <= 10
• nums 中的所有整数 互不相同

代码展示

class Solution {
public:
    void backtrack(vector<vector<int>>& res, vector<int>& output, int first, int len){
        // 所有数都填完了
        if (first == len) {
            res.emplace_back(output); // 当前排列已完成，将其添加到结果集中
            return;
        }
        for (int i = first; i < len; ++i) {
            // 动态维护数组
            swap(output[i], output[first]); // 交换当前位置与第一个位置的数字
            // 继续递归填下一个数
            backtrack(res, output, first + 1, len); // 递归填充下一个位置的数字
            // 撤销操作，即还原数组
            swap(output[i], output[first]); // 恢复交换前的数组状态，进行回溯
        }
    }
    
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> res;
        backtrack(res, nums, 0, (int)nums.size()); // 调用回溯函数开始生成全排列
        return res; // 返回所有全排列结果
    }
};

这段代码使用了递归和回溯的方法来生成全排列。具体解释如下：

• backtrack 函数是回溯的核心部分。它接受以下参数：
  • res：存储结果的二维向量。
  • output：当前正在生成的排列。
  • first：表示当前正在处理的位置。
  • len：数组的长度，用于确定何时完成排列。
• 在 backtrack 函数中，首先检查是否已经生成了一个完整的排列（即 first == len）。如果是，将当前排列添加到结果集 res 中。
• 接下来，使用一个 for 循环，从当前位置 first 开始遍历数组。对于每个位置 i，它进行了以下操作：
  • 交换 output[i] 和 output[first]，这是为了将当前位置的数字放到第一个位置，相当于固定了第一个位置的数字。
  • 然后递归调用 backtrack，处理下一个位置，即 first + 1。
  • 最后，进行回溯，恢复数组状态，即再次交换 output[i] 和 output[first]，以便尝试其他数字排列。
• 最后，在 permute 函数中，它调用了 backtrack 函数，从数组的第一个位置开始生成全排列。最终返回所有生成的全排列。

这段代码是一个经典的全排列生成算法，使用了回溯技巧，通过交换数组中的元素来生成所有可能的排列。

lc47.全排列II–中等

题目描述

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

• 1 <= nums.length <= 8
• -10 <= nums[i] <= 10

代码展示

class Solution {
    vector<int> vis; // 用于标记元素是否已经被使用

public:
    void backtrack(vector<int>& nums, vector<vector<int>>& ans, int idx, vector<int>& perm) {
        if (idx == nums.size()) {
            ans.emplace_back(perm); // 当前排列已完成，将其添加到结果集中
            return;
        }
        for (int i = 0; i < (int)nums.size(); ++i) {
            if (vis[i] || (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1])) {
                // 跳过已使用的元素或者处理重复元素时，跳过非第一个重复元素
                continue;
            }
            perm.emplace_back(nums[i]); // 将当前元素加入当前排列
            vis[i] = 1; // 标记当前元素已使用
            backtrack(nums, ans, idx + 1, perm); // 递归处理下一个位置
            vis[i] = 0; // 回溯，标记当前元素未使用
            perm.pop_back(); // 移除当前元素，以便尝试其他可能的排列
        }
    }

    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<vector<int>> ans;
        vector<int> perm;
        vis.resize(nums.size()); // 初始化标记数组
        sort(nums.begin(), nums.end()); // 对输入数组进行排序，以方便处理重复元素
        backtrack(nums, ans, 0, perm); // 调用回溯函数开始生成全排列
        return ans; // 返回所有生成的不重复全排列
    }
};

lc226.翻转二叉树–简单

题目描述

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

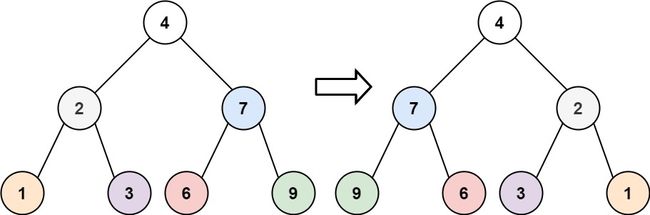
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

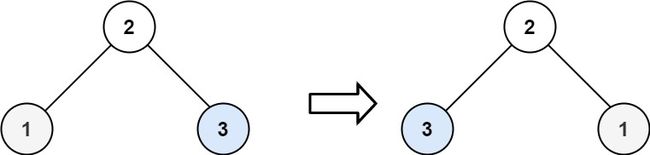
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目范围在 [0, 100] 内
• -100 <= Node.val <= 100

代码展示

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) {
            return nullptr;
        }
        TreeNode* left = invertTree(root->left);
        TreeNode* right = invertTree(root->right);
        root->left = right;
        root->right = left;
        return root;
    }
};

lc98.验证二叉搜索树–中等

题目描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

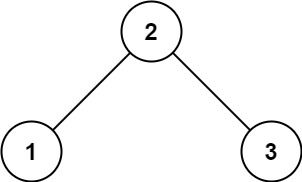
输入：root = [2,1,3]
输出：true

示例 2：

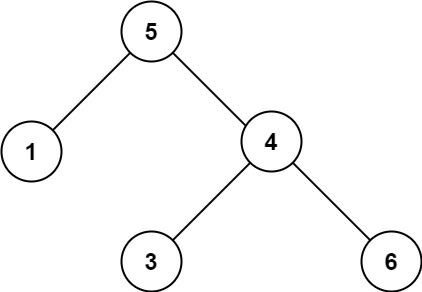
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

代码展示

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:    //递归
    bool helper(TreeNode* root, long long lower, long long upper) {
        if (root == nullptr) {
            return true;
        }
        if (root -> val <= lower || root -> val >= upper) {
            return false;
        }
        return helper(root -> left, lower, root -> val) && helper(root -> right, root -> val, upper);
    }
    bool isValidBST(TreeNode* root) {
        return helper(root, LONG_MIN, LONG_MAX);
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:     //中序遍历
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> stack;
        long long inorder = (long long)INT_MIN - 1;

        while (!stack.empty() || root != nullptr) {
            while (root != nullptr) {
                stack.push(root);
                root = root -> left;
            }
            root = stack.top();
            stack.pop();
            // 如果中序遍历得到的节点的值小于等于前一个 inorder，说明不是二叉搜索树
            if (root -> val <= inorder) {
                return false;
            }
            inorder = root -> val;
            root = root -> right;
        }
        return true;
    }
};

lc104.二叉树的最大深度–简单

题目描述

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 [0, 104] 区间内。
• -100 <= Node.val <= 100

代码展示

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:     // 深度优先搜索
    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        queue<TreeNode*> Q;
        Q.push(root);
        int ans = 0;
        while (!Q.empty()) {
            int sz = Q.size();
            while (sz > 0) {
                TreeNode* node = Q.front();Q.pop();
                if (node->left) Q.push(node->left);
                if (node->right) Q.push(node->right);
                sz -= 1;
            }
            ans += 1;
        } 
        return ans;
    }
};

lc104.二叉树的最小深度–简单

题目描述

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

**说明：**叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

• 树中节点数的范围在 [0, 105] 内
• -1000 <= Node.val <= 1000

代码展示

首先可以想到使用深度优先搜索的方法，遍历整棵树，记录最小深度。

对于每一个非叶子节点，我们只需要分别计算其左右子树的最小叶子节点深度。这样就将一个大问题转化为了小问题，可以递归地解决该问题。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:    //深度优先搜索
    int minDepth(TreeNode *root) {
        if (root == nullptr) {
            return 0;
        }

        if (root->left == nullptr && root->right == nullptr) {
            return 1;
        }

        int min_depth = INT_MAX;
        if (root->left != nullptr) {
            min_depth = min(minDepth(root->left), min_depth);
        }
        if (root->right != nullptr) {
            min_depth = min(minDepth(root->right), min_depth);
        }

        return min_depth + 1;
    }
};

同样，我们可以想到使用广度优先搜索的方法，遍历整棵树。

当我们找到一个叶子节点时，直接返回这个叶子节点的深度。广度优先搜索的性质保证了最先搜索到的叶子节点的深度一定最小。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:    //广度优先搜索
    int minDepth(TreeNode *root) {
        if (root == nullptr) {
            return 0;
        }

        queue<pair<TreeNode *, int> > que;
        que.emplace(root, 1);
        while (!que.empty()) {
            TreeNode *node = que.front().first;
            int depth = que.front().second;
            que.pop();
            if (node->left == nullptr && node->right == nullptr) {
                return depth;
            }
            if (node->left != nullptr) {
                que.emplace(node->left, depth + 1);
            }
            if (node->right != nullptr) {
                que.emplace(node->right, depth + 1);
            }
        }

        return 0;
    }
};

lc50.Pow(x,n)–中等

题目描述

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xn ）。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

• -100.0 < x < 100.0
• -231 <= n <= 231-1
• n 是一个整数
• 要么 x 不为零，要么 n > 0 。
• -104 <= xn <= 104

代码展示

class Solution {
public:
    double myPow(double x, long long n) {
        if (n < 0) return 1 / myPow(x, -n); // 如果 n 是负数，先计算 x 的 -n 次幂，然后取其倒数
        if (n == 0) return 1; // 如果 n 等于 0，返回 1，任何数的 0 次幂都是 1
        double temp = myPow(x, n / 2); // 递归计算 x 的 n/2 次幂
        if (n % 2 == 0)
            return temp * temp; // 如果 n 是偶数，x 的 n 次幂等于 x 的 n/2 次幂的平方
        else
            return temp * temp * x; // 如果 n 是奇数，x 的 n 次幂等于 x 的 n/2 次幂的平方再乘以 x
    }
};

lc22.括号生成–中等

题目描述

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

提示：

• 1 <= n <= 8

代码展示

class Solution {
public:
    // 计数（统计）类的分治问题
    vector<string> generateParenthesis(int n) {
        if (n == 0) return {""};
        // if h.contains(n)
        // 记忆化，避免计算重复的generateParenthesis(n)
        if (h.find(n) != h.end()) return h[n];
        // 划分子问题标准：第一个子问题，作为不可分割的整体
        // 分段方法：(a)b
        // (a)： k对括号，子问题a是k-1对括号
        // b： n-k对括号
        vector<string> result;
        // 不同的k之间：加法原理
        for (int k = 1; k <= n; k++) {
            vector<string> result_a = generateParenthesis(k - 1);
            vector<string> result_b = generateParenthesis(n - k);
            // 左右两个子问题：乘法原理
            for (string& a : result_a)
                for (string& b : result_b)
                    result.push_back("(" + a + ")" + b);
        }
        h[n] = result;
        return result;
    }

private:
    unordered_map<int, vector<string>> h;

    // (a)b
    // ((())) 拆为 a=(())  b=""
    // (())() 拆为 a=()  b=()
    // ()()() 拆为 a=""  b=()()
};

lc23.合并k个升序链表–困难

题目描述

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

输入：lists = []
输出：[]

示例 3：

输入：lists = [[]]
输出：[]

提示：

• k == lists.length
• 0 <= k <= 10^4
• 0 <= lists[i].length <= 500
• -10^4 <= lists[i][j] <= 10^4
• lists[i] 按 升序 排列
• lists[i].length 的总和不超过 10^4

代码展示

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:      //顺序合并
    ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
        if ((!a) || (!b)) return a ? a : b;
        ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
        while (aPtr && bPtr) {
            if (aPtr->val < bPtr->val) {
                tail->next = aPtr; aPtr = aPtr->next;
            } else {
                tail->next = bPtr; bPtr = bPtr->next;
            }
            tail = tail->next;
        }
        tail->next = (aPtr ? aPtr : bPtr);
        return head.next;
    }

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        ListNode *ans = nullptr;
        for (size_t i = 0; i < lists.size(); ++i) {
            ans = mergeTwoLists(ans, lists[i]);
        }
        return ans;
    }
};

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:       //分治合并
    ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
        if ((!a) || (!b)) return a ? a : b;
        ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
        while (aPtr && bPtr) {
            if (aPtr->val < bPtr->val) {
                tail->next = aPtr; aPtr = aPtr->next;
            } else {
                tail->next = bPtr; bPtr = bPtr->next;
            }
            tail = tail->next;
        }
        tail->next = (aPtr ? aPtr : bPtr);
        return head.next;
    }

    ListNode* merge(vector <ListNode*> &lists, int l, int r) {
        if (l == r) return lists[l];
        if (l > r) return nullptr;
        int mid = (l + r) >> 1;
        return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
    }

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        return merge(lists, 0, lists.size() - 1);
    }
};