数据结构进阶篇,回文字符串专题
5. 最长回文子串
「题目」:
给你一个字符串 s,找到 s 中最长的回文子串。
「示例」:
输入:s = "babad",输出:"bab"。
「解题思路」:
首先,判断一个字符串是否为回文字符串,可以采用 双指针 的方式来处理,需要消耗 O(n) 的时间复杂度。
如果使用首尾向中心扫描的策略,那么就需要 O(n^2) 的时间复杂度来确定子串,而更换为由中心向两边扫描的策略,则只需要 O(n) 的时间复杂度即可确定子串。
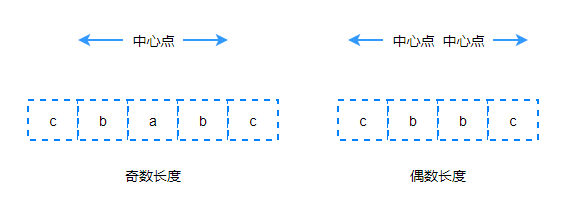
首尾向中心扫描的策略是基于子串确定的前提下,所以不需要考虑字符串的奇偶性。而中心扩展算法只有在识别到首尾字符不一致的情况,才能确定当前子串,而对于奇数长度的字符串和偶数长度的字符串,它们的中心点是不一样的:
奇数长度字符串的中心点:Math.floor(len / 2)。
偶数长度字符串的中心点:len / 2 - 1 和 len / 2。
时间复杂度:O(n^2),空间复杂度:O(1)。
const longestPalindrome = (s) => {
if (!s) {
return ''
}
let start = 0;
let end = 0;
for (let i = 0; i < s.length; i++) {
const odd = expandAroundCenter(s, i - 1, i + 1);
const even = expandAroundCenter(s, i, i + 1);
const len = Math.max(odd.len, even.len);
if (len > end - start) {
if (odd.len === len) {
start = odd.left;
end = odd.right;
} else {
start = even.left;
end = even.right;
}
}
}
return s.substring(start, end + 1);
}
function expandAroundCenter (s, left, right) {
while (left >= 0 && right < s.length && s[left] === s[right]) {
--left;
++right;
}
return {
left: left + 1,
right: right - 1,
len: right - left - 1
}
}131. 分割回文串
「题目」:
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文串 。返回 s 所有可能的分割方案。
「示例」:
输入:s = "aab",输出:[["a","a","b"],["aa","b"]]。
「解题思路」:
由于题目要求返回所有的分割方案,所以只能采用回溯的方式进行枚举。
由于本道题的第一个回文字符串的起点是固定的,所以只能采用首尾向中心扫描的算法来判断当前子串是否为回文字符串。
时间复杂度:O(n2^n),空间复杂度:O(2^n)。
const partition = s => {
const max = s.length
const ans = []
const path = []
backtrack(s, 0, path, ans, max);
return ans
}
function backtrack(str, position, path, ans, max) {
if (position === max) {
return ans.push([...path]);
}
for (let i = position; i < max; i++) {
if (isPalindrome(str, position, i)) {
path.push(str.substring(position, i + 1))
backtrack(str, i + 1, path, ans, max);
path.pop();
}
}
}
function isPalindrome(str, start, end) {
while (start < end) {
if (str[start] === str[end]) {
start++;
end--;
} else {
return false;
}
}
return true;
}516. 最长回文子序列
「题目」:
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
「示例」:
输入:s = "bbbab";输出:4;解释:一个可能的最长回文子序列为 "bbbb" 。
「解题思路」:
最值问题可以通过动态规划来进行记忆化枚举,用 dp[i][j] 表示字符串下标范围 [i, j] 内最大回文子序列的长度。
首先对于任意长度为1的子序列来说,其都是回文子序列,即 dp[i][i] = 1。
当 i < j 时,只需要考虑 s[i] 和 s[j] 是否相等即可:
s[i] === s[j]:此时 [i, j] 范围内的子序列为回文子序列,即 dp[i][j] = dp[i + 1][j - 1] + 2。
s[i] !== s[j]:此时 s[i] 和 s[j] 不可能同时作为回文子序列的首尾,那么此时 dp[i][j] 最长回文子序列应该存在于 dp[i + 1][j] 或者是 dp[i][j - 1] 中,即 dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1])。
由上述推导过程可以知道,i 应该从后往前遍历,因为需要执行 i + 1 的状态转移;j 应该向后遍历,应为需要执行 j - 1 的状态转移。
时间复杂度:O(n^2),空间复杂度:O(n^2)。
const longestPalindromeSubseq = function(s) {
const max = s.length
const dp = Array(max).fill(0).map(() => Array(max).fill(0))
for (let i = max - 1; i >= 0; i--) {
dp[i][i] = 1;
const c1 = s[i];
for (let j = i + 1; j < max; j++) {
const c2 = s[j];
if (c1 === c2) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
return dp[0][max - 1];
};647. 回文子串
「题目」:
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
「示例」:
输入:s = "abc",输出:3,解释:三个回文子串: "a", "b", "c"。
「解题思路」:
本道题目可以采用《5. 最长回文子串》的解题思路,并且由于本题只需要求解数目,所以不涉及额外状态的保存,解题代码显得更加清晰。
时间复杂度:O(n^2),空间复杂度:O(1)。
var countSubstrings = function(s) {
let ans = 0;
const max = s.length;
for (let i = 0; i < max; i++) {
ans++;
let start = i - 1;
let end = i + 1;
while (start >= 0 && end < max && s[start] === s[end]) {
ans++;
start--;
end++;
}
}
for (let i = 1; i < max; i++) {
let start = i - 1;
let end = i;
while (start >= 0 && end < max && s[start] === s[end]) {
ans++;
start--;
end++;
}
}
return ans;
};写在最后
「感谢您能耐心地读到这里,如果本文对您有帮助,欢迎点赞、分享、或者关注下方的公众号哟。」
相关链接:
最长回文子串 https://leetcode-cn.com/problems/longest-palindromic-substring/
分割回文串 https://leetcode-cn.com/problems/palindrome-partitioning/
最长回文子序列 https://leetcode-cn.com/problems/longest-palindromic-subsequence/
回文子串 https://leetcode-cn.com/problems/palindromic-substrings/