前缀和与差分

前缀和与差分

1. 前缀和

前缀和 是指某序列的前n项和，可以把它理解为数学上的数列的前n项和

1.1 一维前缀和

P6568 水壶

n = int(input().strip())
m = int(input().strip())
nums = list(map(int,input().strip().split()))
arr = [0]*(n+1)
for i in range(n):
    arr[i+1] = arr[i]+nums[i]
ans = 0
j = 1
while j+m <= n:
    ans = max(arr[j+m]-arr[j-1],ans)
    j += 1
print(ans)

1.2 二维前缀和

先给出问题：
输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和。

同一维前缀和一样，我们先来定义一个二维数组 $s$,$s[i][j]$ 表示二维数组中，左上角(1, 1)到右下角(i, j)所包围的矩阵元素的和。接下来推导二维前缀和的公式。

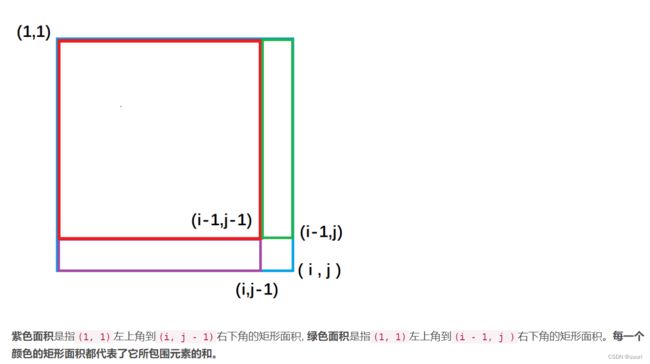
接下来去求以(x1,y1)为左上角和以(x2,y2)为右下角的矩阵的元素的和:

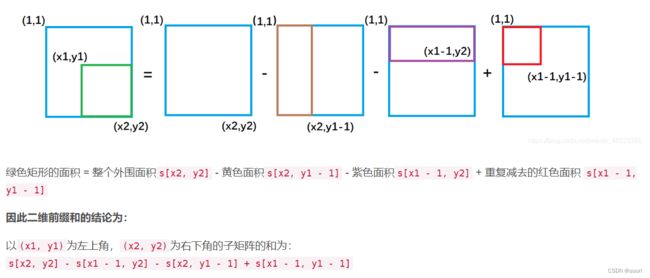
总结：

P2004 领地选择

n,m,c = map(int,input().strip().split())
sum = [[0 for i in range(m+1)] for i in range(n+1)]

for i in range(1,n+1):
    sum[i] = [0]+list(map(int,input().strip().split()))

for i in range(1,n+1):
    for j in range(1,m+1):
        sum[i][j] = sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+sum[i][j]

max =-0xfffffff

for i in range(c,n+1):
    for j in range(c,m+1):
        k = sum[i][j]-sum[i][j-c]-sum[i-c][j]+sum[i-c][j-c]
        if k > max:
            max = k
            x,y = i-c,j-c
print(x+1,y+1,sep=" ")

2. 差分

差分可以看成前缀和的逆运算

2.1 一维差分

考虑如何构造差分b数组？

差分数组作用：

我们画个图理解一下这个公式的由来:


总结：

2.1.1 例题 AcWing 797. 差分

输入一个长度为 $n$ 的整数序列。
接下来输入 $m$ 个操作，每个操作包含三个整数 $l,r,c$，表示将序列中 $[l,r]之间的每个数加上c。$
请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数 $n和m。$
第二行包含 $n$ 个整数，表示整数序列。
接下来 $m$ 行，每行包含三个整数 $l，r，c，$表示一个操作。
输出格式
共一行，包含 $n$ 个整数，表示最终序列。
数据范围：
$1\le n,m\le 100000$
$1\le l\le r\le n$
输入样例：

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例：

3 4 5 3 4 2

代码：

n,q = map(int,input().split())
a = [0]+list(map(int,input().split()))
b = [0]*(n+1)
for i in range(q):
	l,r,c = map(int,input().split())
	b[l] += c
	b[r+1] -= c

for i in range(1,n+1):
	b[i] += b[i-1] 
	print(b[i])

2.2 二维差分

扩展到二维，我们需要让二维数组被选中的子矩阵中的每个元素的值加上 c,也可以达到 $O(1)$ 的时间复杂度。

$a[][]数组是b[][]数组的前缀和数组，那么b[][]是a[][]的差分数组$

原数组：$a[i][j]$

我们去构造差分数组： $b[i][j]$

使得 $a$ 数组中 $a[i][j]$ 是 $b$ 数组左上角 $(1,1)$ 到右下角 $(i,j)$ 所包围矩形元素的和。

如何构造 $b$ 数组:

从图中我们可以很清晰发现 $a_{ij}$ 就是 $b$ 矩阵中 $b_{ij}$ 往左往上所有元素（包括 $b_{ij}$ 所在行所在列）的值的总合，显然往右进行的是前缀和，那么我们怎么用数学表达式表示呢？

上图表示了一般情况，那么我们可以得到下面的等式：
$$a_{i,j}=a_{i-1,j}+a_{i,j-1}-a_{i-1,j-1}+b_{i,j}$$
这个等式就将前缀和矩阵和差分矩阵联系在一起，同时体现了迭代思维，由 $a_{i,j}$ 之前的值求自身，然后自身又作为已知的值求下一个值，这样我们通过已知差分矩阵Bn得到前缀和矩阵An，同样我们通过该式也可以通过前缀和矩阵An求差分矩阵Bn：
$$b_{i,j}=a_{i,j}-a_{i,j-1}-a_{i-1,j}+a_{i-1,j-1}$$

例题 2.2.1 P3397 地毯

n, m = map(int, input().split())
ls = [[0] * (n + 1) for _ in range(n + 1)]

for _ in range(m):
    x1, y1, x2, y2 = map(int, input().split())
    ls[x1][y1] += 1
    ls[x2 + 1][y1] -= 1
    ls[x1][y2 + 1] -= 1
    ls[x2 + 1][y2 + 1] += 1

ans = [[0] * (n + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
    for j in range(1, n + 1):
        ans[i][j] = ans[i -  1][j] + ans[i][j - 1] - ans[i - 1][j - 1] + ls[i][j]
        print(ans[i][j], end = " ")
    print()

二维差分 转成 一维差分：

n,m=map(int,input().strip().split())
a=[[0]*(n+10) for _ in range(n+10)]

for i in range(m):
    x1,y1,x2,y2=map(int,input().strip().split())
    for j in range(x1,x2+1): # 把每行单独看作一维差分
        a[j][y1] += 1
        a[j][y2+1] -= 1

for i in range(1,n+1):
    for j in range(1,n+1):
        a[i][j] += a[i][j-1]
        print(a[i][j],end=" ")
    print()

3. 例题

3.1 P3406 海底高铁

注意索引

n,m = map(int,input().split())
Cities = list(map(int,input().split()))

ls = [0]*n
for i in range(1,m):
    x,y = Cities[i-1],Cities[i]
    r = max(x,y)
    l = min(x,y)
    ls[l-1] += 1
    ls[r-1] -= 1 # 只乘坐到 站r的前一条铁路

ans = 0
t = 0
for i in range(n-1):
    a,b,c = map(int,input().split())
    t += ls[i]
    ans+= min(a*t,b*t+c)
print(ans)

3.2 P5542 [USACO19FEB]Painting The Barn S

n,k = map(int,input().split())

ls = [[0]*1010 for i in range(1010)]
ans=0
minx,maxx = 1010,0
miny,maxy = 1010,0
for i in range(n):
    x1,y1,x2,y2 = map(int,input().split())
    minx = min(minx,x1)
    maxx = max(maxx,x2)
    miny = min(miny,y1)
    maxy = max(maxy,y2)
    for j in range(x1,x2):
        ls[j][y1] +=1
        ls[j][y2]-=1

for i in range(minx,maxx+1):
    for j in range(miny,maxy+1):
        ls[i][j]+=ls[i][j-1]
        if ls[i][j]==k:
            ans+=1
print(ans)

3.3 P4552 [Poetize6] IncDec Sequence

思路：

要使得序列的数全部相等，其实就是让他们之间的差全为0，也就是差分序列的除了第一项每一项都是0；
由于题目要求最少的步骤，我们可以考虑，如果差分序列里有一个正数和一个负数（出现的顺序无所谓），那么我们优先对这个正数和负数进行操作，为什么呢？因为我们有以下两个公式：

• 如果a[l,r]+1，则b[l]+1，b[r+1]-1
• 如果a[l,r]-1，则b[l]-1，b[r+1]+1

正数-1，负数+1，这样相当于一步里作用了两步，比让正数一个个-1和让负数一个个+1快多了
那么我们可以进行多少种这样的操作呢？

我们可以令差分序列里正数绝对值的总和为 p，负数绝对值总和为 q ，可以进行这样一步顶两步的操作就是 min(p,q)，因为这种操作正数负数是一一配对的，当少的那个先用完了，剩下的没有可以配对的了，只能一步步减或一步步加。

所以我们总共要进行的操作就为min(p,q)+abs(p-q)，也就是max(p,q)

第二问
保证最少次数的前提下，最终得到的数列有多少种？

得到的数列有多少种，其实就是问的 b[1] 可以有多少种,我们上述所有操作是与 b[1] 无关的，因为我们的目标是让除了 b[1] 以外的项变 0，所以我们上述的操作没有考虑到 b[1]，b[1] 怎么变，与我们求出的最小步骤无关那么，我们怎么知道 b[1] 有几种呢？
很简单，其实就是看看有几种一步步减或一步步加的操作数，

• 因为我们一步步加的时候（假设我们现在的操作对象下标为 i ），可以这样操作，b[1]-1 或 b[i]+1
• 一步步减的时候可以这样操作，b[1]+1 或 b[i]-1

所以说，有几步一步步的操作就有几种情况+1，为什么+1呢，因为这个b[1]本身就有一个值，就算你不对他进行任何操作，它自己也有一种情况。

一加一减（也就是我们所说的一步顶两步的操作）操作数为 min(p,q)，那么一步步的操作数就为max(p,q) - min(p,q) = abs(p,q)

n = int(input())
a = [int(input()) for i in range(n)]
a = [0]+a
b = [0]*(n+1)
for i in range(1,n+1):
    b[i] = a[i]-a[i-1]

pos,neg = 0,0
for c in b[2:]:
    if c>0:
        pos+=1
    else:
        neg+=1

print(min(pos,neg))
print(1+abs(pos-neg))

3.4 P2280 [HNOI2003]激光炸弹

此题数据读入存在问题

n,m = map(int,input().split())
ls = [[0]*(n+10) for i in range(n+10)]

for i in range(n):
    x,y,v = map(int,input().split())
    ls[x+1][y+1] = v

s = [[0]*(n+10) for i in range(n+10)]

for i in range(1,n+1):
    for j in range(1,1+n):
        s[i][j] = s[i-1][j]+s[i][j-1]-s[i-1][j-1]+ls[i][j]

ls = 0
ans = 0

for i in range(m,n+1):
    for j in range(m,n+1):
        k = s[i][j]-s[i-m][j]-s[i][j-m]+s[i-m][j-m]
        ans = max(k,ans)

print(ans)

3.5 P7994 [USACO21DEC] Air Cownditioning B

贪心

n = int(input())
p = [0]+list(map(int,input().split()))
t = [0]+list(map(int,input().split()))

b = [0]*(n+1)
for i in range(1,n+1):
    b[i] = p[i]-t[i]

ans1,ans2 = 0,0

for i in range(1,n+1):
    if b[i]>b[i-1]:
        ans1+=b[i]-b[i-1]
    else:
        ans2 += b[i-1]-b[i]
print(max(ans1,ans2))