4.查找算法（python）

写在前面
小弟初识数据结构与算法，本文是个人的学习记录

4.1 算法综述

查找(Searching)的主要作用是通过一定的方法，在一些(有序或无序的)数据元素中找出与给定关键值相同的数据元素

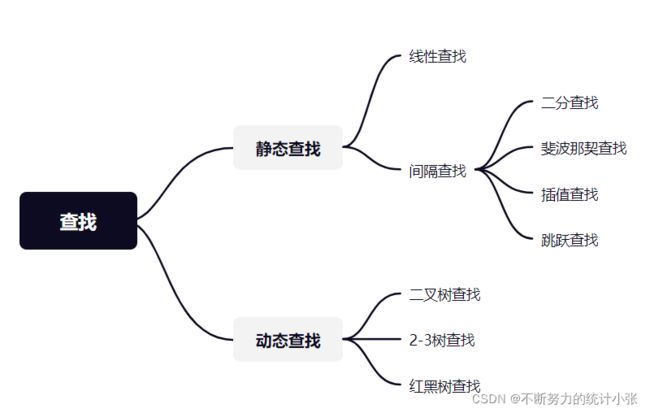
按照操作方式可分成两种类别：

• 静态查找表：仅进行查找操作，不能改变表中的数据元素
• 动态查找表：在查找的同时进行创建、扩充、修改、删除等操作

具体的：

查找算法特性：

算法	结构	时间复杂度	ASL(平均查找长度)	最坏情况查找长度
线性查找	随意	O(N)	(N+1)/2	N+1
二分查找	有序	O(logN)	log(N+1)-1	logN
跳跃查找
斐波那契查找
插值查找
二叉树查找
2-3树查找
红黑树查找
哈希查找

一般情况下，查找算法不需要辅助空间，因此空间复杂度可以不考虑

4.2 线性查找

4.2.1 定义

线性查找又称顺序查找，是一种最简单的查找方法，核心思想是从第一个元素开始，逐个比较关键值，直到找到目标元素，则查找成功；若遍历整个序列都没有找到目标元素，则查找失败

1.复杂度分析

平均查找长度（Average Search Length，ASL）：$ASL=1/N(1+2+3+...+N)=(N+1)/2$

当查找不成功时，即最坏情况下，需要N+1次比较，故时间复杂度为O(N)

2.优点

无序查找，列表不需要有序

4.2.2 代码实现

def linear_search(arr, key):
    '''线性查找'''
    for i, value in enumerate(arr):
        if value == key:
            return i # 如果找到，结束程序，返回元素下标i
    else:
        return -1 # 没有找到

Python内置函数：

• max()：寻找最大值
• index()：寻找元素对应下标

i = arr.index(max(arr))

4.3 间隔查找

间隔查找有一个前提：原始序列必须有序

4.3.1 二分查找

二分查找也称为折半查找，其基本思想是：

• 从表的中间元素开始，与目标元素比较：

  • 若相等：则查找成功
  • 若目标元素比中间元素大，则把查找区间定位在表的后半段
  • 若目标元素比中间元素小，则把查找区间定位在表的前半段

• 然后用相同的方法找到中间元素继续比较，直到找到目标元素

• 如果查找区间的左右边界出现异常，则查找失败

1.复杂度分析

二分查找法每次排除一半的不合适值，所以对于N个元素：每次循环数量减半

最坏情况下即第x次在N/(2^x)中查找，解出$x=logN$

故时间复杂度为$O(logN)$

平均查找长度为$((N+1)log(N+1)-N)/N$，约等于$log(N+1)-1$

注：log函数都以2为底；平均查找长度计算过程参考：https://blog.csdn.net/turne/article/details/50488378

2.优缺点

比较次数少，查找速度快，平均性能好；但是要求待查表为有序表，且插入删除困难

因此，二分查找方法适用于不经常变动而查找频繁的有序列表

3. 代码实现

程序的核心，while循环的两个退出条件：

• 找到目标元素：arr[mid] == key
• 左右边界重合：first > last

def binary_search(arr, key):
    '''
    二分查找算法
    
    arr: 输入列表
    key: 待查找元素
    '''
    # 初始化
    first = 0 # 最小值下标（左边界）
    last = len(arr) - 1 # 最大值下标（右边界）
    index = -1 # 记录目标值下标
    
    while (first <= last) and (index == -1):
        mid = (first + last) // 2 # 计算中间元素下标
        if arr[mid] == key:
            index = mid  # 找到目标元素，记录下标
        else:
            if key < arr[mid]:
                last = mid - 1 # 若小于中间元素，则看前半部分，修改右边界的值
            else:
                first = mid + 1 # 若大于中间元素，则看后半部分，修改左边界的值
    return index

4.3.2 斐波那契查找

斐波那契数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….（从第三个数开始，后边每一个数都是前两个数的和）

$$F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n>=2)$$

斐波那契查找就是在二分查找算法的基础上，把数列分为两部分，其大小为连续的斐波那契数值：

• 首先找到大于或等于给定查找表长度的最小斐波那契数值，找到斐波那契数值为$F[n]$（第n个斐波那契数）
• 若$F[n]-1$大于查找表长度，则需要补充最后一个元素，知道满足$F[n]-1$个元素
• 然后使用$F[n-1]-1$的值作为索引（如果有效），然后将此数列上的值与目标元素进行比较
• 若目标元素比较大，就找后半部分，否则找前半部分
• 重复这个一过程，不断缩小这一过程，直到找到目标元素

1. 复杂度分析

时间复杂度为$O(logN)$，平均查找长度小于二分查找，最坏情况查找长度大于二分查找

2. 优缺点

斐波那契查找只需要使用加法和减法，在数据量较大时优势更明显

3. 代码实现

def fibonacci_search(arr, key):
    '''斐波那契查找算法'''
    # 初始化斐波那契数列
    fib_N_2 = 0 # F(k-2)
    fib_N_1 = 1 # F(k-1)
    fib_next = fib_N_1 + fib_N_2 # F(n)=F(n-1)+F(n-2)
    length =len(arr) # 原始序列的长度
    
    # 找到一个斐波那契数列值不小于序列的长度
    while (fib_next < length):
        fib_N_2 = fib_N_1
        fib_N_1 = fib_next
        fib_next = fib_N_2 + fib_N_1
    # 记录下标的漂移量
    offset = -1
    
    # 当fib_next小于1时，表示没有序列可以拆分，查找结束
    while (fib_next > 1):
        # 找出中间元素的下标，但要确保下标不越界
        i = min(offset + fib_N_2, length - 1)
        # 如果中间元素比目标元素小，获取后半部分
        if (arr[i] < key):
            fib_next = fib_N_1
            fib_N_1 = fib_N_2
            fib_N_2 = fib_next - fib_N_1
            offset = i # 下标漂移量为i
        elif (arr[i] > key):
            fib_next = fib_N_1
            fib_N_1 = fib_N_2
            fib_N_2 = fib_next - fib_N_1
        else:
            return i # 刚好相等，返回元素下标
    # 最后和最大元素值比较
    if (fib_N_1 and offset < length - 1) and (arr[offset+1] == key):
        return offset+1
    return -1 # 没有找到元素，返回-1

# 测试
arr = [10,20,40,50,60,70,90]
print(fibonacci_search(arr, 70))
print(fibonacci_search(arr, 77))

结果：
5
-1

斐波那契查找和二分查找本质上一样，只是分割点不同:

• 二分查找算法计算中间分隔值用’//'整除
• 斐波那契查找计算中间分割值只用了加减

理论上，斐波那契查找优于二分查找

4.3.3 插值查找

插值查找是对二分查找的改造，将查找点的选择改进为自适应选择，可以提高查找效率

插值查找选择中间元素的公式如下：

$$index=low+[(key-arr[low])\ast (high-low)/(arr[high]-arr[low])]$$

算法思路：计算出目标元素所在序列的占比，然后确定分割位置，达到自适应的效果

• 当目标元素更接近右边界时，下标偏向右边，反之偏向左边
• 然后找出index下标对应的元素值，并和目标元素比较
• 如果比目标元素大，则取左边子序列，反之取右边子序列
• 重复这一过程，直到找到目标元素，或者边界异常

1. 复杂度分析

时间复杂度为$O(log(logN))$，平均查找长度小于二分查找，最坏情况查找长度为$O(logN)$

2. 优缺点

对于分布比较均匀的序列，效率高；反之，效率低

3. 代码实现

while循环的两个退出条件：

• 找到目标函数：index != -1
• 列表边界错误：low >= high

def interpolation_search(arr, key):
    '''插值查找算法'''
    low = 0 # 最小值下标
    high = len(arr) - 1 # 最大值下标
    index = -1 # 记录目标值下标，若找不到返回-1
    
    while(low < high) and (index == -1):
        # 计算中间元素下标
        mid = low + int((high - low) * (key - arr[low]) / (arr[high] - arr[low]))
        if arr[mid] == key:
            index = mid
        else:
            if key < arr[mid]:
                # 若小于中间元素，则看前半部分，修改右边界的值
                high = mid - 1
            else:
                # 若大于中间元素，则看后半部分，修改左边界的值
                low = mid + 1
    return index 

测试：
arr = [10,20,40,50,60,70,90]
print(interpolation_search(arr, 70))
print(interpolation_search(arr, 77))

结果：
5
-1

4.3.4 跳跃查找

跳跃查找是通过固定步骤跳过某些元素代替搜索所有元素来检查较少的元素（而不是线性搜索），它是间隔查找和线性查找的融合，因此也只能针对有序序列

最佳步长：数组长度的开方

因为：最坏的情况下，如果最后检查的值大于要查找的元素，必须跳 n/m 次，然后再执行线性查找 m-1 次。因此最坏情况下的比较总数为((n/m) + m-1)，在m=n的开方时，函数((n/m) + m-1)的值最小

1. 复杂度分析

时间复杂度为$O(\sqrt{n})$，平均查找长度大于二分查找，最坏情况查找长度为$2\ast sqrt(N)-1$

2. 代码实现

import math

def jump_search(arr, key):
    '''跳跃查找'''
    length = len(arr) 
    jump = int(math.sqrt(length)) # 计算跳跃长度,也是子序列长度
    left, right = 0,0
    while left < length and arr[left] <= key:
        # 找到目标元素所在子序列
        right = min(length - 1, left + jump - 1) # 找到右边界下标
        if arr[left] <= key and arr[right] >= key: # 目标元素是否在子序列中
            break # 如果是，跳出循环
        left += jump # 否则跳到下一个子序列
        
    if left >= length or arr[left] > key:
        return -1 # 没有找到
    right = min(length-1, right) # 找到子序列边界
    
    # 在子序列中进行线性查找
    for i, value in enumerate(arr[left:right+1]):
        if value == key:
            return i + left # 加上左边界的值才是原始序列的下标
    return -1 # 找不到

测试：
arr = [10,20,30,40,50,60,70,80,90]
print(jump_search(arr,40))
print(jump_search(arr,90))
print(jump_search(arr,41))

结果：
3
8
-1

4.3.5 案例

计算每个位置距离洒水点的距离，然后找到这些距离中的最短距离，一共有以下4种情况：

• 位置点和洒水点位置相同，则距离为0
• 洒水点在位置点左侧，则可以认为这是最近的距离
• 洒水点在位置点右侧，则需要和位置点左侧的洒水点比较距离长短，取距离最短的
• 洒水点都在位置点右侧，那么将最近的洒水点作为最近距离

1. 数据规模和算法复杂度

查找洒水点距离选用二分查找法，如果位置点有M个，洒水点有N个，那么算法的时间复杂度为$O(MlogN)$；空间上并不需要额外辅助空间，只需记录最长距离即可，因此空间复杂度为O(1)

2. 代码实现

def find_min_radius(points, water):
    # 存放最长距离
    max_length = 0
    # 二分查找法的前提是有序序列，这里使用内置函数排序
    points.sort()
    water.sort()
    
    for p in points:
        # 二分查找
        left = 0
        right = len(water) - 1
        while left < right:
            mid = (left + right) // 2
            if water[mid] < p:
                left = mid + 1
            else:
                right = mid
        # 情况1：若找到的值等于p，则说明p处有一个洒水点，p到洒水点的最短距离为0
        if water[left] == p:
            continue
            
        # 情况2：若该洒水点的坐标值小于p，说明该洒水点的坐标与p之间没有其他洒水器
        elif water[left] < p:
            if max_length < p - water[left]:
                max_length = p - water[left]
        
        # 情况3：若该洒水点的坐标值大于p并且left不等于0，说明p介于left和left-1之间
        elif left > 0:
            # 该位置到洒水点的最短距离就是left和left-1处洒水点与p插值的最小值
            tmp_res = min(water[left] - p, p - water[left -1])
            if max_length < tmp_res:
                max_length = tmp_res
        
        # 情况4：left =0，即所有洒水点都比p点大
        else:
            if max_length < water[left] - p:
                max_length = water[left] - p
        print(max_length)
    return max_length

测试：
points = [2,4,1,6,12,8]
water = [3,4,5,11]
find_min_radius(points,water)

结果：
2
2
2
3 
3
return ：3

4.4 树表查找

线性查找和间隔查找都属于静态查找算法，查找过程中不会改变存储结构

动态查找算法通过构建特定的数据结构来提高查找效率，数表查找是比较常见的动态查找，包括二叉树查找、红黑树查找

4.4.1 二叉树查找

一般情况下，构建二叉查找树需要的插入和删除操作比排序少

二叉查找树也称二叉搜索树、二叉排序树，它有以下性质：

左子树所有值 <= 双亲节点的值 <= 右子树所有值

但二叉树有一个缺点，如果输入序列接近有序，构建出来的二叉树有可能不平衡，这样会使查找效率迅速降低

此时，查找效率将变为O(N)

4.4.2 平衡树

平衡查找树可以保证树在插入完成之后始终保持平衡状态，即便最差的情况下也能达到$O(logN)$的效率

1. 2-3查找树

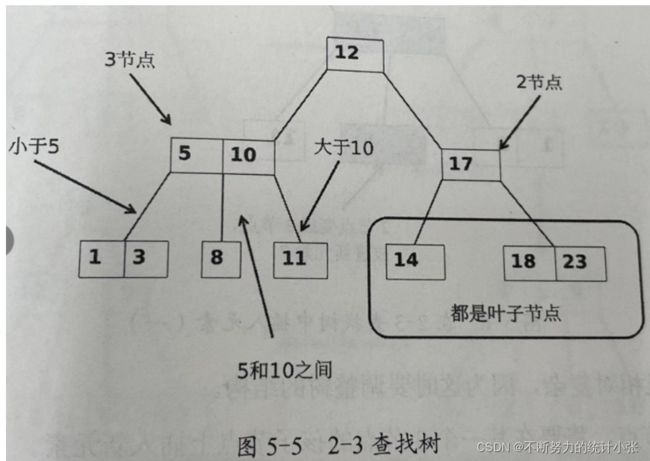
2-3查找树基于2-3树的树形结构，其内部节点有两种：

• 普通的2节点(2-node)：保存了一个数据元素和左右两个孩子节点
• 3节点(3-node)：保存两个数据元素和三个叶子节点，并且有一个或者两个数据元素

若没有找到目标元素，则要把该元素插入树中，正因为有3节点的设定，才能有空间缓存新插入的节点，才有调整的可能性

2节点插入

2节点插入相对简单，直接把2节点变成3节点，然后把新元素放在该节点上即可，类似于缓存效果

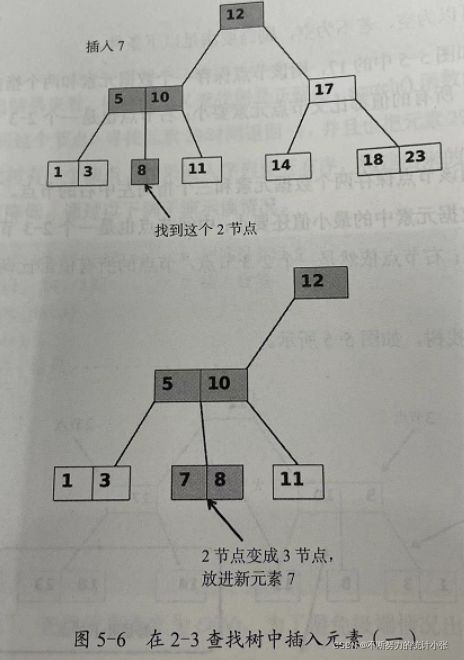
3节点插入

(1)父节点是2节点，将要在其一个3节点的孩子节点上插入新元素

类似2节点的插入过程，临时把新元素放在该节点上，这时该节点上有三个元素，把中间元素提升到父节点上，父节点变为3节点，最后把剩下的两个元素放在新的3节点适当的孩子节点上

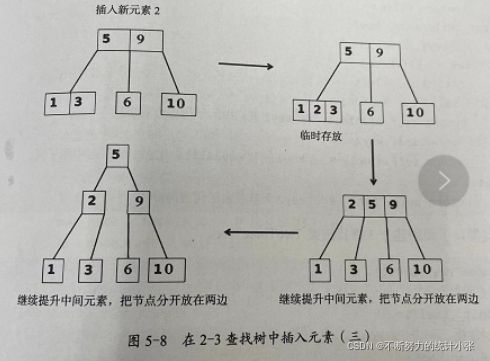
(2)父节点是3节点，将要在其一个3节点的孩子节点上插入新元素
首先按照上一种情况的方式把新元素临时安放在该节点上，然后把中间元素提升到父节点，这时父节点拥有三个元素，因此还需要继续调整，把中间元素向上提升，使其成为父节点

然后把左右两边的元素分别放到两边的孩子节点上

class Node(object):
    '''创建2-3查找树节点类'''
    def __init__(self, key):
        self.key1 = key # 至少一个值，那么最多是两个孩子节点
        self.key2 = None # 保存两个key，那么有可能是三个孩子节点
        self.left = None
        self.middle = None
        self.right = None
    def __repr__(self):
        return '2_3TreeNode({},{})'.format(self.key1, self.key2)
    
    def is_leaf(self):
        # 是否为叶子节点
        return self.left is None and self.middle is None and self.right is None
    
    def has_key2(self):
        # 是否有key2
        return self.key2 is not None
    
    def has_key(self, key):
        # 2-3查找树是否存在该值
        if (self.key1 == key) or (self.key2 is not None and self.key2 == key):
            return True
        else:
            return False
    
    def get_child(self, key):
        # 小于key1,查找左边子树
        if key < self.key1:
            return self.left
        elif self.key2 is None:
            return self.middle # 没有key2就把中间子树作为右子树
        elif key < self.key2:
            return self.middle # 有key2就和key2比较，比它小就是在中间子树
        else:
            return self.right # 比key2大，就往右子树方向寻找

创建2-3查找树类

class TwoThreeTree(object):
    """2-3查找树类"""
    def __init__(self):
        # 初始化，根结点为None
        self.root = None
    def is_empty(self): # 是否为空
        return self.root is None
    def get(self, key):
        # 获取结点
        if self.is_empty():
            return None  # 如果是空，当然没有结果
        else:
            return self._get(self.root, key)
    def _get(self, node, key):  # _表示私有函数概念
        if self.is_empty():
            return None
        elif node.has_key(key): # None在逻辑判断中相当于False
            # 如果有返回结果，则停止寻找，返回结果
            return node
        else:
            child = node.get_child(key) # 若没有找到继续尝试寻找孩子结点
            return self._get(child, key)
    def search(self, key):
        # 查找结点，有则返回True，没有则返回False
        if self.get(key):
            return True
        else:
            return False
    def insert(self, key):
        # 插入结点
        if self.is_empty(): # 如果是空，直接赋值给根结点
            self.root = Node(key)
        else:
            # 否则根据之前我们分析情况去进行插入，p_key和p_ref可以表示为临时保存
            p_key, p_ref = self._insert(self.root, key)
            if p_key is not None:
                # 这里是最上层了，如果还有新插入的元素，
                # 则需要把中间元素升为根结点
                # 然后把剩下的两个元素拆分两边放在左子树(left)和中间子树(middle)
                new_node = Node(p_key) # 这是提升的元素
                new_node.left = self.root
                new_node.middle = p_ref
                self.root = new_node   # 变成根结点
    def _insert(self, node, key):
        if node.has_key(key): # 已经存在结点则无需再插入
            return None, None
        elif node.is_leaf(): # 如果是叶子结点,可以尝试插入
            return self._add_to_node(node,key, None)
        else:
            # 不是叶子结点继续寻找孩子结点
            child = node.get_child(key) # 比较插入值大小，判断往哪个子树寻找位置
            p_key, p_ref = self._insert(child, key) # 递归尝试插入
            if p_key is None: # 没有新插入元素，则无需处理
                return None,None
            else:
                # 否则就需要尝试插入到该结点
                return self._add_to_node(node, p_key, p_ref)
    def _add_to_node(self, node, key, p_ref):
        if node.has_key2(): # 如果已经有两个key，需要插入新元素后拆分剩余的元素
            return self._split_node(node, key, p_ref)
        else:
            # 第一种情况，只有一个key的结点
            if key < node.key1:   # 如果新元素比key1大，则代替key1,key1变为key2
                node.key2 = node.key1
                node.key1 = key
                if p_ref is not None: # 如果有新孩子结点
                    node.right = node.middle # 原来在中间子树移动到右子树
                    node.middle = p_ref # 中间子树指向新孩子结点
            else:
                node.key2 = key  # 否则新元素为key2
                if p_ref is not None: # 新孩子结点放在最右边
                    node.right = p_ref
            return None,None
    def _split_node(self, node, key, p_ref):
        # 当结点有3元素的时候，我们需要提升中间元素为父结点，拆分剩下的两个元素
        # 左边元素原用之前的结点，右边元素用新结点
        new_node = Node(None) # 新结点是给右边元素
        if key < node.key1: # 如果新元素比key1小，那么就提升key1
            p_key = node.key1         # key1为提升元素
            node.key1 = key           # 新插入元素原用key1结点
            new_node.key1 = node.key2 # key2是右边新元素
            if p_ref is not None: # 如果新孩子结点
                new_node.left = node.middle # 原结点的中间子树成为新结点左子树
                new_node.middle = node.right # 原结点的右子树成为新结点中间子树
                node.middle = p_ref # 把中间子树指向新孩子结点
        # 如果新元素大于key1，小于key2，那么就提升新插入元素key
        elif key < node.key2:
            p_key = key               # key为提升元素
            new_node.key1 = node.key2 # key2是右边新元素
            if p_ref is not None:
                new_node.left = p_ref # 把左子树指向新孩子结点
                new_node.middle = node.right
        else:
            # 如果新插入元素大于key2，那么就提升key2
            p_key = node.key2    # key2为提升元素
            new_node.key1 = key  # key1是右边新结点
            if p_ref is not None:
                new_node.left = node.right # 原结点的右子树成为新结点左子树
                new_node.middle = p_ref    # 新孩子结点成为新结点中间子树
        node.key2 = None        # 提升后，原结点成为了2结点
        return p_key, new_node  # 返回提升元素和新的孩子结点

测试：

t = TwoThreeTree()
for i in [5,9,1,3,6,10]:
    t.insert(i)
    
print("根结点：", t.root)
print("根结点左子树：", t.root.left)
print("根结点中间子树：", t.root.middle)
print("根结点右子树：", t.root.right)
t.insert(2)  # 插入新元素2
print("当前根结点：",t.root)

结果：
根结点： 2_3TreeNode(5,9)
根结点左子树： 2_3TreeNode(1,3)
根结点中间子树： 2_3TreeNode(6,None)
根结点右子树： 2_3TreeNode(10,None)
当前根结点： 2_3TreeNode(5,None)

2. 红黑树

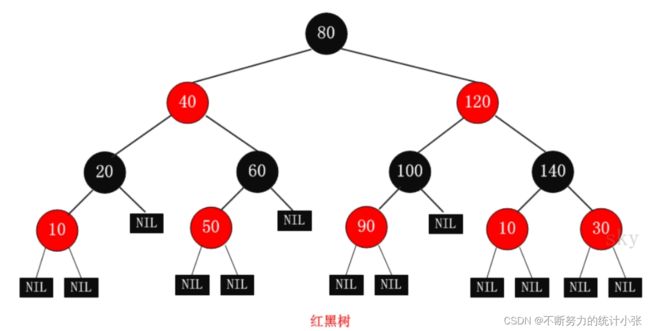
红黑树在进行插入和删除操作时，通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能，红黑树的特性如下：

• 每一个节点都有颜色，即红色或者黑色
• 根节点是黑色
• 叶子节点不包含数据，但不是多余的，用来保持红黑树的结构特征
• 如果是红色节点，那么它的孩子节点都是黑色
• 从任一节点到其每个叶子节点的所有路径都包含相同的黑色节点

红黑树的表示

class Node():
    '''定义红黑树节点类'''
    def __init__(self, data):
        self.data = data # 元素值
        self.parent = None # 父亲节点
        self.left = None # 左子节点
        self.right = None # 右子节点
        self.color = 1 # 颜色1是红色，0是黑色
        
    def __repr__(self):
        from pprint import pformat # 格式化打印
        if self.left is None and self.right is None:
            # 如果没有孩子节点，就输出本节点的元素值和颜色
            return "'%s %s'" % (self.data, (self.color and "红色") or "黑色")
        
        # 有孩子节点，先输出本节点的元素值和颜色，再用()包含孩子节点的输出
        return pformat(
            {
                "%s %s"
                % (self.data, (self.color and "红色") or "黑色"): (self.left, self.right)
            },
            indent = 1,
        )

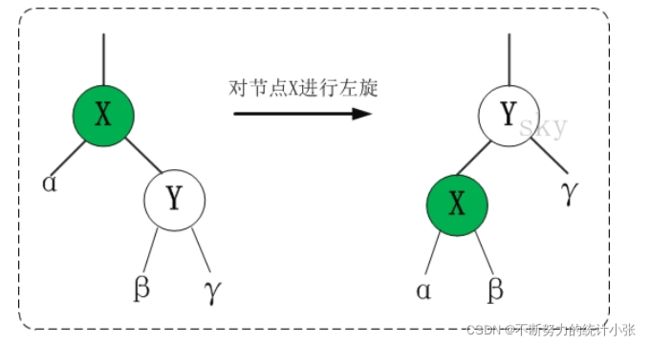
为了保持其自身平衡，让树保持红黑树的特性，红黑树的操作一共有三种：左旋、右旋和变色

(1) 左旋

左旋中的“左”，意味着“被旋转的节点将变成一个左节点”

以X作为支点，其右孩子节点Y变成支点的父节点，右孩子节点的左子树$\beta$变成支点X的右子树，其右子树$\gamma$不变

左旋的伪代码《算法导论》：

def left_rotate(self, x):
    '''左旋'''
    y = x.right  # 定义y为x的右孩子节点
    x.right = y.left  # 支点x的右子树为y的左子树
     
    if y.left != self.NONE:  # β不是NONE
        y.left.parent = x # β的父节点从y变为x
    y.parent = x.parent # Y作为支点
    
    if x.parent == None: # x为根节点
        self.root = y
        
    elif x == x.parent.left: # x为左孩子节点
        x.parent.left = y
    
    else:
        x.parent.right = y 
    
    y.left = x
    x.parent = y

(2) 右旋

右旋中的“右”，意味着“被旋转的节点将变成一个右节点”

右旋的伪代码《算法导论》：

def right_rotate(self, y):
    '''右旋'''
    x = y.left
    y.left = x.right
    
    if x.right != self.NONE:
        x.right.parent = y
    x.parent = y.parent
    
    if y.parent == None:
        self.root = x
    elif y == y.parent.right:
        y.parent.right = x
    else:
        y.parent.left = x
        
    x.right = y
    y.parent = x

(3) 变色

旋转后的二叉树不再符合红黑树的特性，因此需要改变颜色

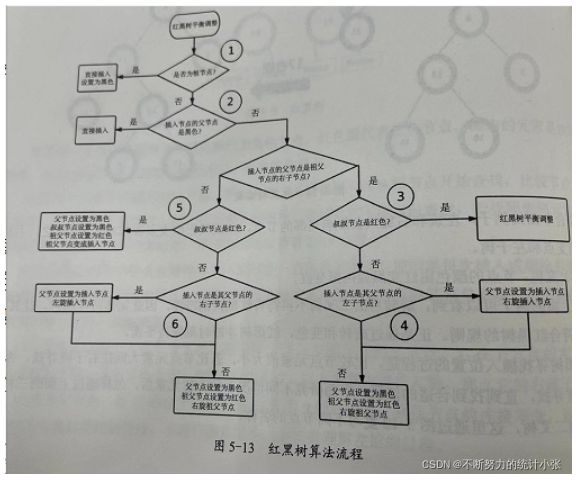
(4) 插入操作

步骤：

• 将红黑树当作一颗二叉查找树，将节点插入
• 将节点着色为红色，不会违背特性：从任一节点到其每个叶子节点的所有路径都包含相同的黑色节点
• 通过旋转和重新变色等方法来修正该树，使之重新成为一颗红黑树，使其满足特性：如果是红色节点，那么它的孩子节点都是黑色

根据被插入节点的父节点的情况，划分为三种情况来处理：

• 红黑树为空，即插入的新元素是根节点：直接把此节点涂为黑色
• 插入节点的父节点为黑色：直接插入，不需要调整
• 插入节点的父节点为红色：情况相对复杂

核心：将红色的节点移到根节点；然后，将根节点设为黑色

class RedBlackTree():
    '''红黑树类'''
    def __init__(self):
        # 定义叶子节点NONE
        self.NONE = Node(None)
        self.NONE.color = 0 # 叶子节点一定是黑色
        self.root = self.NONE
    
    def __search_help(self, node, key):
        if node == self.NONE or key == node.data:
            return node
        if key < node.data:
            return self.__search_help(node.left, key) # 左子树查找
        return self.__search_help(node.right, key)  # 右子树查找
    
    def search(self, k):
        '''寻找元素'''
        return self.__search_help(self.root, k)
    
    def __fix_insert(self, k):
        '''插入新元素后的调整'''
        while k.parent.color == 1: # 第三种情况，插入节点的父节点是红色
            if k.parent == k.parent.parent.right:  # 父节点是祖父节点的右节点
                uncle = k.parent.parent.left # 获取叔叔节点
                if uncle.color == 1:
                    # 案例1：父节点和叔叔节点为红色
                    # 红黑树平衡调整
                    uncle.color = 0 # 叔叔节点变为黑色
                    k.parent.color = 0 # 父节点变为黑色
                    k.parent.parent.color = 1 # 祖父节点变为红色
                    k = k.parent.parent # 插入节点变为祖父节点
                
                else:
                    if k == k.parent.left:
                        # 案例3：插入节点的父节点是祖父节点的右子节点
                        # 并且插入节点是其父节点的左子节点
                        k = k.parent # 插入点改为父节点
                        self.right_rotate(k) # 右旋
                        
                    # 案例2：插入节点的父节点是祖父节点的右子节点
                    # 并且插入节点是其父节点的右子节点
                    k.parent.color = 0 # 父节点变为黑色
                    k.parent.parent.color = 1 # 祖父节点变为红色
                    self.left_rotate(k.parent.parent) # 左旋祖父节点
                
            # 父节点是祖父节点的左节点
            else:
                uncle = k.parent.parent.right # 获取叔叔节点
                if uncle.color == 1:
                    # 与案例1一样
                    uncle.color = 0
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    k = k.parent.parent
                else:
                    if k == k.parent.right:
                        # 案例3 镜像处理
                        k = k.parent
                        self.left_rotate(k)
                    # 案例2 镜像处理
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    self.right_rotate(k.parent.parent)
            if k == self.root: # 插入节点是根节点，不需要继续处理
                break
        self.root.color = 0 # 最后确保根节点是黑色
        
    def left_rotate(self, x):
        '''左旋'''
        y = x.right  # 定义y为x的右孩子节点
        x.right = y.left  # 支点x的右子树为y的左子树

        if y.left != self.NONE:  # β不是NONE
            y.left.parent = x # β的父节点从y变为x
        y.parent = x.parent # Y作为支点

        if x.parent == None: # x为根节点
            self.root = y

        elif x == x.parent.left: # x为左孩子节点
            x.parent.left = y

        else:
            x.parent.right = y 

        y.left = x
        x.parent = y
    
    def right_rotate(self, y):
        '''右旋'''
        x = y.left
        y.left = x.right

        if x.right != self.NONE:
            x.right.parent = y
        x.parent = y.parent

        if y.parent == None:
            self.root = x
        elif y == y.parent.right:
            y.parent.right = x
        else:
            y.parent.left = x

        x.right = y
        y.parent = x
        
    
    
    def insert(self, key):
        '''插入新元素，先插入合适的位置
            算法如二叉查找树，然后调整节点，实现平衡'''
        node = Node(key) # 定义新元素节点
        node.parent = None
        node.data = key
        node.left = self.NONE
        node.right = self.NONE
        node.color = 1 # 新节点一定是红色
        
        y = None
        x = self.root
        
        while x != self.NONE:
            y = x # 记录x当前节点
            if node.data < x.data:
                x = x.left
            else:
                x = x.right
            
        # 找到合适的空位置
        node.parent = y
        if y == None:
            self.root = node
        elif node.data < y.data:
            y.left = node
        else:
            y.right = node
            
        if node.parent == None:
            # 如果父节点是空，说明它是根节点，直接改变颜色
            node.color = 0
            return 
        if node.parent.parent == None:
            # 如果祖父节点是空，则说明是根节点的字节点
            # 根据定义，父节点是黑色，直接插入
            return 
        self.__fix_insert(node) # 其他情况需要调整节点
        
    def get_root(self):
        return self.root

测试：

rbt = RedBlackTree()
rbt.insert(40)
rbt.insert(32)
rbt.insert(75)
rbt.insert(50)
rbt.insert(90)

print("插入新元素前:",  rbt.get_root())
rbt.insert(98)
print("插入新元素后：", rbt.get_root())

结果：
插入新元素前: 2_3TreeNode(40,None)
插入新元素后： 2_3TreeNode(40,None)

4.4.3 案例

根据规则，当用户设置密码时，系统调用程序检查密码，若不符合要求，就为用户改造密码，然后直接返回新密码；若符合要求，则返回用户设置的密码

强密码条件：

• 至少由八个字符组成
• 至少包含一个小写字母、一个大写字母和一个数字
• 同一字符不能连续出现三次

修改：

• 字符不够，自动补充随机特殊字符，直到满足最少字符个数
• 小写、大写字母、数字三种类别的字符，若没有其中哪种，自动随机添加一个该类别字符
• 如果出现连续的同一字符，在第三个相同字符面前插入一个随机特殊字符
• 特殊字符按照python字符类中的string.punctuation确定范围

1. 问题核心

遍历密码字符串，发现字符串的组合特征，如有多少个大写字母、多少个小写字母、多少个数字，是否有连续的字符、总字符有多少；然后根据定义去修改密码字符串

为了尽量减少对用户密码的修改，判断条件和修改密码的步骤需要有一定的顺序：

1. 先判断是否缺少一类字符
2. 再判断是否出现连续的同一字符
3. 最后检查是否满足最小字符数量

2. 算法复杂度

遍历一次字符串可以修正是否包含三种字符类型，遍历第二次字符串可以拆开连续的相同字符，因此时间复杂度为O(2N)；在修改连续字符串时，一般不会在循环中插入新的元素，所以用一个新的列表记录修改后的新密码，因此空间复杂度为O(N)

3. 代码实现

from random import randint, sample 
import string

special_characters = list(string.punctuation)  # 特殊字符列表

def strong_password(password):
    password = list(password)
    # 先看是否有三种类型的字符
    has_uppercase = False # 是否有大写字母
    has_lowercase = False # 是否有小写字母
    has_digits = False # 是否有数字
    
    for letter in password:
        if letter in string.ascii_uppercase:
            has_uppercase = True
            continue
        if letter in string.ascii_lowercase:
            has_lowercase = True
            continue
        if letter in string.digits:
            has_digits = True
            continue
        if has_uppercase and has_lowercase and has_digits:
            break # 如果已经符合要求，就不需要继续查找
            
    # 是否需要补充字符
    if not has_uppercase:
        position = randint(0, len(password)-1) # 生成随机位置
        letter = string.ascii_uppercase[randint(0, 25)] # 生成随机大写字符
        password.insert(position, letter)
    
    if not has_lowercase:
        position = randint(0, len(password)-1) # 生成随机位置
        letter = string.ascii_lowercase[randint(0, 25)] # 生成随机大写字符
        password.insert(position, letter)
        
    if not has_digits:
        position = randint(0, len(password)-1)
        letter = str(randint(0,9))
        password.insert(position, letter)
        
    # 检查是否有连续的相同字符
    new_password = password.copy()
    same_letter_count = 1 # 统计出现次数
    add_count = 0 # 插入新元素数量
    
    for i in range(0, len(password)):
        if i > 0:
            if password[i] == password[i-1]:
                same_letter_count += 1 
            else:
                same_letter_count = 1 
        if same_letter_count > 2:
            letter = special_characters[randint(0, len(special_characters) - 1)]
            new_password.insert(i + add_count, letter)
            add_count += 1
            same_letter_count = 1
    
    # 字符数量是否不小于八个
    while len(new_password) < 8:
        letters = sample(special_characters, 8 - len(new_password)) # 随机抽样n个特殊字符
        new_password += "".join(letters) # 若不够八个，补足
    return "".join(new_password)

测试：

print(strong_password("test1"))
print(strong_password("123456"))
print(strong_password("111111"))
print(strong_password("password"))
print(strong_password("Aabc1234"))

结果：
teCst1%/
U123t456
T11`11w11
1passwoSrd
Aabc1234