文献阅读:Raise a Child in Large Language Model: Towards Effective and Generalizable Fine-tuning
- 文献阅读:Raise a Child in Large Language Model: Towards Effective and Generalizable Fine-tuning
- 1. 内容简介
- 2. 相关工作
- 1. Weight Decay
- 2. Top-K Tuning
- 3. Mixout
- 4. RecAdam
- 5. R3F
- 3. 优化方案
- 1. ChildTuning-F
- 2. ChildTuning-D
- 4. 实验设计 & 结果
- 1. ChildTuning效果考察
- 2. 泛化能力考察
- 3. Tuning策略横向对比
- 4. 小数据场景考察
- 5. 消解实验
- 5. 结论 & 思考
文献链接:https://arxiv.org/pdf/2109.05687v1.pdf
1. 内容简介
这篇文章是上年罗福莉组发的一篇关于预训练模型调优方面的工作。
众所周知,当前在nlp领域,基于大语料预训练然后再在特定领域进行finetune已经成为了一个相对标准化的任务范式,几乎刷爆了当前所有任务的sota指标。
但是,大模型下finetune的过程就成了一个复杂的炼丹过程,不同的任务下参数调整的幅度,learning rate下降的速率都是一个很大的学问,他们归根结底都是因为不同参数在不同的任务下对于结果的敏感性不同,而模型的规模过大导致模型的表达能力实在太强,因此稍微训练一下就容易过拟合,或者破坏掉模型预训练学到的内容,使得模型丧失泛化能力。
这点在transfer learning当中非常常见,但是预训练模型的范式显然放大了这方面的问题。
针对这个点,其实也有了不少的工作,我自己也曾经做过一些transfer learning相关的工作,所以也想过对应的问题,不过不得不说,罗福莉她们在这篇文章中给出的方法还是很巧妙,非常的trivial但是somehow很make sense,事实上也获得了非常好的效果,不得不佩服啊。
2. 相关工作
在讨论她们的方案之前,我们不妨先看一下这篇文献中提及的其他一些优化思路:
1. Weight Decay
这个方法来源于文章:Frustratingly Easy Domain Adaptation
这个方法的主要思路就是通过正则项来控制finetune之后的参数改动幅度。
他的方法本身倒是比较简单,就是在loss当中加入了正则项 λ ⋅ ∣ ∣ w − w 0 ∣ ∣ 2 \lambda \cdot ||w - w_0||^2 λ⋅∣∣w−w0∣∣2。通过这种方式就可以人为的限制参数改动的幅度整体不会特别大,从而尽可能地保留预训练模型学习到的先验信息。
2. Top-K Tuning
这个方法来源于文章:Parameter-Efficient Transfer Learning for NLP
Top-K tuning的方法让我有一种无比的熟悉感,因为我当年就是这么干的,虽然我当时并不了解这篇文章,只是直觉上就觉得应该这么干……
他的方法可能是这里所有的方法当中最为直接的了,因为他就是直接freeze了预训练的模型,然后只训练最后的决策层当中的参数。通过这种方式,就可以最大化的保留下预训练模型学习到的信息。
3. Mixout
这个方法来源于文章:Mixout: Effective Regularization to Finetune Large-scale Pretrained Language Models
Mixout这个工作和上述两个方法也是异曲同工,不过他的方法是说在每一轮训练中随机将其部分参数替换为初始化的预训练参数,a.k.a,令模型在训练与没有训练之间反复横跳,从而达到薛定谔的优化态[doge]……
4. RecAdam
这个方法来源于文章:Recall and Learn: Fine-tuning Deep Pretrained Language Models with Less Forgetting
这个方法看起来脱胎于Weight Decay,他的思路就是将Weight Decay当中的超参 λ \lambda λ随时演化,不断调整正则项在loss函数中的权重占比。
新的loss函数如下:
L = λ ( t ) ⋅ L C E ( w ) + ( 1 − λ ( t ) ) ⋅ ∣ ∣ w − w 0 ∣ ∣ 2 L = \lambda(t) \cdot L_{CE}(w) + (1-\lambda(t)) \cdot ||w-w_0||^2 L=λ(t)⋅LCE(w)+(1−λ(t))⋅∣∣w−w0∣∣2
其中,随时演化的 λ ( t ) \lambda(t) λ(t)函数表达式为:
λ ( t ) = 1 1 + C ⋅ e − k ⋅ t \lambda(t) = \frac{1}{1 + C \cdot e^{-k \cdot t}} λ(t)=1+C⋅e−k⋅t1
其中, C C C和 k k k为超参。
显然,当 t = 0 t=0 t=0时, λ ( t ) \lambda(t) λ(t)最小,此时模型收到正则项的限制最大,模型需要在初始参数的监督之下慢慢训练,而当训练经过了足够的步数之后,特定任务和预训练参数之间的gap已经被磨平了,此时就可以放心大胆的忘掉正则项让模型好好地学习特定任务的特征了。
5. R3F
这个方法来源于文章:Better Fine-Tuning by Reducing Representational Collapse
这个方法的核心思路同样是通过正则项来限制模型在训练中不至于彻底破坏预训练过程学习到的参数分布。
不过,不同于Weight Decay以及RecAdam,它使用KL散度作为正则项,具体loss函数定义如下:
L ( w ) = L C E ( w ) + λ K L S ( f ( x ) ∣ ∣ f ( x + z ) ) L(w) = L_{CE}(w) + \lambda KL_S(f(x) || f(x+z)) L(w)=LCE(w)+λKLS(f(x)∣∣f(x+z))
其中, f ( x ) f(x) f(x)为模型函数,而z是一个随机采样的噪声分布,一般控制其为正态分布 N ( 0 , σ ) N(0, \sigma) N(0,σ)或者均匀分布 U ( − σ , σ ) U(-\sigma, \sigma) U(−σ,σ)。
3. 优化方案
综上所述,上述所有的方法其实本质上要实现的目标都是:
- 限制finetune过程的参数变化幅度,让模型尽可能地保留预训练学习到的内隐信息的前提下学习到特定任务的参数分布。
而这里,罗福莉她们的思路也完全相同,但是她们采用的方法某种意义上来说也更加直接。
她们的出发点就是说显然预训练模型这么大,超参这么多,对于一个特定的任务,那么必然大部分的参数事实上都是没有什么贡献的,此时如果我们finetune了这部分的参数,那么它对于整体的模型训练将不会产生正向的收益,反而会导致模型丧失预训练中学到的先验信息。
因此,她们提出了ChildTuning方法,即每次都从全部参数之中筛选出一个子网络,然后仅仅对这部分网络的参数进行更新。这样,就可以实现我们在上面提出的优化目标。
但是,显然的,这里就会涉及到一个问题,就是如何挑选出这个子网络。
对于这个问题,她们提出了两种ChildTuning方法,即ChildTuning-F和ChildTuning-D。
下面,我们来具体看一下这两种方式。
1. ChildTuning-F
ChildTuning-F的参数筛选方式非常的暴力,就是按照伯努利分布随机选择一些参数进行梯度mask。即是说,给出一个超参p,然后对于每一个模型参数,其都有p的概率被mask而不会进行梯度更新。
坦率地说,ChildTuning-F我个人不太能理解,想不到什么定性的解释能够直观的描述为啥这种方法能够生效,但是somehow罗福莉她们给出了一个数学上的证明,说明这种方式可以在使得模型训练收敛到一个更加稳定的局域最小值,并且可以有更小的误差范围。
至于其数学证明,这里就不班门弄斧了,有兴趣的读者可以自行去看一下他们在附录中给出的证明。
2. ChildTuning-D
ChildTuning-D在直觉上就make sense很多,就是给出一个超参 P D P_D PD,然后每次只更新对全部参数中对于任务影响最大的前 p D p_D pD的参数进行梯度更新。
那么剩下的问题就是,如何来定义参数重要性。这里,她们使用Fisher Information来进行参数重要性的定义,其对应的公式如下:
F ( w ) = 1 ∣ D ∣ ⋅ ∑ j = 1 D ( ∂ l o g p ( y j ∣ x j ; w ) ∂ w ) 2 F(w) = \frac{1}{|D|} \cdot \sum_{j=1}^{D} (\frac{\partial log p(y_j | x_j ; w)}{\partial w})^2 F(w)=∣D∣1⋅j=1∑D(∂w∂logp(yj∣xj;w))2
而后我们只需要根据 F ( w ) F(w) F(w)对参数进行排序,然后取前 p D p_D pD比例的数据进行梯度更新即可。
4. 实验设计 & 结果
现在,我们来看一下文中针对ChildTuning进行的实验考察。
1. ChildTuning效果考察
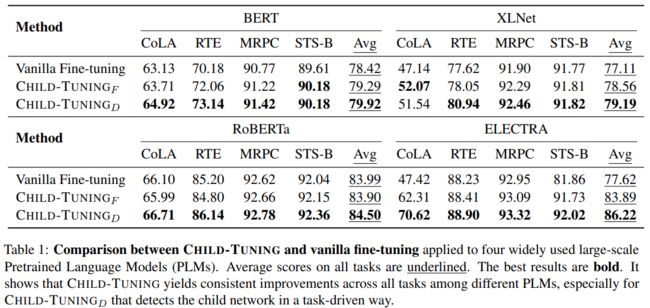
首先,是惯例的模型效果考察,无论想法多么的fascinating,没有效果那么都是扯淡。但是ChildTuning确实给出了非常牛逼的结果,她们分别基于bert、roberta、xlnet以及electra四种模型在GLUE的多个子任务下进行评测,发现ChildTuning均优于传统的finetune方法(结果如下图所示),这个结果很有说服力了,非常的nice。
2. 泛化能力考察
再然后,我们来考察作者宣称的ChildTuning具备的泛化能力是否存在。
针对这个问题,文中给出了两种考查方式:
-
finetune和评测使用不同的数据
这里的评测方式就是首先在任务数据集A当中进行finetune,然后使用得到的模型直接到任务数据集B当中进行评测。
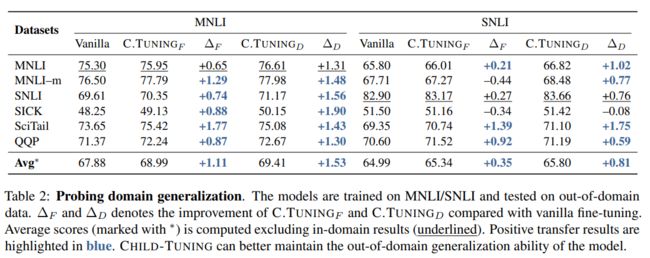
给出结果如下图所示:
可以看到:
- ChildTuning几乎没有翻车过,基本都完虐了vanilla finetune的模型,且提升幅度基本都高于原版。
-
freeze参数然后加入dense层进行transfer learning
这里给出的评测方式与上面稍有不同,他是先用MRPC任务数据集进行finetune,然后freeze参数,之后直接在模型上加入一个dense层之后放到其他的任务当中取训练,然后考察模型的效果。
结果如下图所示:
可以看到:
- ChildTuning依然稳稳地没有翻车。
综上,结合上述两个系列的实验,我们有理由相信ChildTuning确实在泛化性上有着更好的性能表达。
3. Tuning策略横向对比
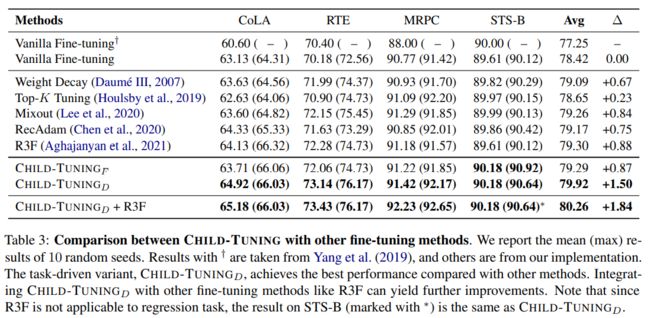
然后,我们将ChildTuning与其他的finetune策略合到一起进行横向比较,得到结果如下:
可以看到,结果依然很稳,说明ChildTuning至少在tuning效果上是优于其他tuning策略的。
4. 小数据场景考察
此外,作者还在小数据集上跑了一下结果,得到结果如下:
说明模型可以在小数据集上得到更好地训练,不太容易出现过拟合的现象。
5. 消解实验
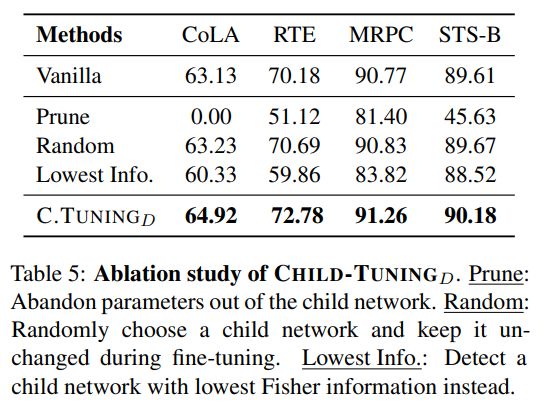
最后,作者还通过消解实验来验证了一下使用Fisher Information来评估参数的重要性确实是一个可靠的方法,其具体的实验结果如下:
5. 结论 & 思考
综上,整体这篇文献真的是惊艳到了我,无论是方法还是实验结果,都成功让我眼前一亮,尤其在现在巨多的工作都需要用到大模型 + finetune的标准范式的情况下,这个方法真的可以做到无缝衔接。
这边已经在尝试将它应用到我的实际工作当中了,希望它能够确实的work吧。^ - ^