区间树
1概要
一个区间树是一个二叉树,它有一个由区间构成的集合S,其中取S中所有区间最左边的端点l和所有区间最右边的端点r,再取两者的中点记做Xmed,对于S中由Xmed穿过的区间集合,称为SMed,对SMed由Xmed,进行左右划分,分为ML和MR,分别表示SMed中所有区间被Xmed所截的左右区间的集合,如下图:
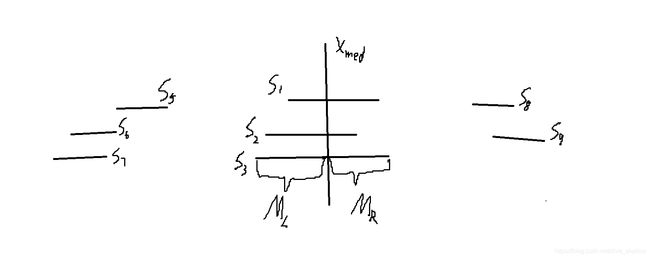
上图中S5,S6,S7称为LMed,S8和S9称为RMed,也就是S是由LMed,SMed和RMed组成,对于根节点root,SMed为S1,S2,S3,而LMed,RMed分别为root的左右子树上的S。
2构建区间树
2.1构建区间树的文字描述
构建区间树的文字描述如下:
输入:给定一个由[li,ri]表示的区间集合S,其中i = 1,...,n。
如果S为空,则区间树为空叶。否则分配一个带有两个子结点的结点v。
对于结点v,计算{l1,...,ln,r1,...rn}的中值Xmed,这意味着一半的区间端点位于Xmed的左侧,一半的区间端点位于Xmed的右侧。(中值一般不等于li或ri)。
令LMed表示XMed左边的集合,令SMed表示包含Xmed的区间集合,令RMed表示Xmed右边的区间集合。
在根v处,存储XMed并为SMed所有左边的端点构建排序列表ML,为SMed所有右边的端点建立排序列表MR。
递归地为v的子结点构建LMed和RMed的区间树。
2.2构建区间树的代码:
(详细解释看最后的源代码)
void IntervalTree::BuildTree(int depth,vector& source)
{
int l = 1<<30,r = -1*(1<<30);
//vector lMed,rMed;
//找出l,r
for(vector::iterator i = source.begin(); i < source.end(); i++)
{
if(i->l < l)
{
l = i->l;
}
if(i->r > r)
{
r = i->r;
}
}
int m = (l + r)/2;
xMed = m;
int cnt = 0;
for(vector::iterator i = source.begin(); i < source.end(); i++)
{
if(m <= i->l)
{
//构建LMed的元素
rMed.push_back(*i);
}
else if(m >= i->r)
{
//构建RMed的元素
lMed.push_back(*i);
}
else
{
//构建SMed,ML和MR
sMed.push_back(*i);
Interval* lInterval = new Interval(i->l,m,sMed[cnt]);
mL.push_back(*lInterval);
Interval* rInterval = new Interval(m,i->r,sMed[cnt]);
mR.push_back(*rInterval);
cnt++;
}
}
sort(mL.begin(),mL.end(),LSortFunc);
sort(mR.begin(),mR.end(),RSortFunc);
if(depth == 1)
{
lTree = NULL;
rTree = NULL;
return;
}
//递归构建左右子树
if(lMed.size() > 0)
{
lTree = new IntervalTree();
lTree->BuildTree(depth - 1, lMed);
}
else
lTree = NULL;
if(rMed.size() > 0)
{
rTree = new IntervalTree();
rTree->BuildTree(depth - 1, rMed);
}
else
rTree = NULL;
}
2.3建区间树的时间复杂度
书上写的是O(nlogn),其实也很好想,对于n个区间,想要从中间穿过所有区间,最多需要建logn层的树,对于每一次遍历,都需要遍历n个区间集合,所有层上加起来一共是对n个区间集合的快速排序,排序肯定不超过nlogn,这样算下来的确是nlogn。
3穿刺查询
3.1穿刺查询的定义
输入:在线条(Line)上的闭合区间集S。
查询:单个值xq∈R
输出:所有区间I∈S,其中xq∈I。
##3.2穿刺查询的描述
输入:给定区间树的根v和查询点xq∈R。
如果xq
如果xq>Med,那么:1.按递减顺序扫描右边端点的排序列表MR并报告所有被穿刺的线段。如果xq大于当前右边的端点,则停止。2.继续使用RMed的区间树递归。
3.2穿刺查询的代码实现
(详细解释看最后的源代码)
void IntervalTree::PiercingQuery(int x)
{
if(x <= xMed)
{
for(vector::iterator i = mL.begin(); i < mL.end(); ++i)
{
if(x < i->l)
{
break;
}
cout<<*(i->parent);
}
}
if(x > xMed)
{
for(vector::iterator i = mR.begin(); i < mR.end(); ++i)
{
if(x > i->r)
{
break;
}
cout<<*(i->parent);
}
}
if(lTree)
lTree->PiercingQuery(x);
if(rTree)
rTree->PiercingQuery(x);
}
3.3穿刺查询时间复杂度
O(k + logn),k为xq穿过的区间个数,n为区间总数。
4源代码
#include
using namespace std;
class Interval
{
public:
//区间的左右端点
int l;
int r;
//SMed中的一个区间被XMed穿过会分为LM中的元素和LR中的元素,parent表示输入LM或者LR的当前的这个区间元素是由SMed中的哪个区间得来的
Interval* parent;
Interval(){}
Interval(int l,int r,Interval parent)
{
this->l = l;
this->r = r;
//这个是为了防止指向函数执行过程中局部变量后,函数运行完,变量内存释放后,指针有问题
this->parent = new Interval();
this->parent->l = parent.l;
this->parent->r = parent.r;
}
Interval(int l,int r)
{
this->l = l;
this->r = r;
}
friend ostream& operator<<(ostream& output,Interval interval);
};
class IntervalTree
{
public:
//定义XMed,SMed,LMed,RMed,ML,MR
int xMed;
vector sMed;
vector mL;
vector mR;
vector lMed;
vector rMed;
IntervalTree* lTree;
IntervalTree* rTree;
void BuildTree(int depth,vector& source);
void PiercingQuery(int x);
};
//ML需要按左端点从小到大排序
bool LSortFunc(const Interval& i1,const Interval& i2);
//MR需要按右端点从大到小排序
bool RSortFunc(const Interval& i1,const Interval& i2);
int main()
{
vector source;
int n;
cin>>n;
int t = n;
while(t--)
{
int l,r;
cin>>l>>r;
Interval* interval = new Interval(l,r);
source.push_back(*interval);
}
IntervalTree* root = new IntervalTree();
//创建logn层的区间树
root->BuildTree(log(n)/log(2),source);
root->PiercingQuery(9);
root->PiercingQuery(4);
root->PiercingQuery(15);
return 0;
}
ostream& operator<<(ostream& output,Interval interval)
{
output< i2.r;
}
void IntervalTree::BuildTree(int depth,vector& source)
{
int l = 1<<30,r = -1*(1<<30);
//找出l,r,方便确定xMed
for(vector::iterator i = source.begin(); i < source.end(); i++)
{
if(i->l < l)
{
l = i->l;
}
if(i->r > r)
{
r = i->r;
}
}
int m = (l + r)/2;
xMed = m;
int cnt = 0;
//比较S中的区间和xMed的关系
for(vector::iterator i = source.begin(); i < source.end(); i++)
{
if(m <= i->l)
{
//构建LMed的元素
rMed.push_back(*i);
}
else if(m >= i->r)
{
//构建RMed的元素
lMed.push_back(*i);
}
else
{
//构建SMed,ML和MR
sMed.push_back(*i);
Interval* lInterval = new Interval(i->l,m,sMed[cnt]);
mL.push_back(*lInterval);
Interval* rInterval = new Interval(m,i->r,sMed[cnt]);
mR.push_back(*rInterval);
cnt++;
}
}
//对ML和MR排序
sort(mL.begin(),mL.end(),LSortFunc);
sort(mR.begin(),mR.end(),RSortFunc);
if(depth == 1)
{
lTree = NULL;
rTree = NULL;
return;
}
//递归构建左右子树
if(lMed.size() > 0)
{
lTree = new IntervalTree();
lTree->BuildTree(depth - 1, lMed);
}
else
lTree = NULL;
if(rMed.size() > 0)
{
rTree = new IntervalTree();
rTree->BuildTree(depth - 1, rMed);
}
else
rTree = NULL;
}
void IntervalTree::PiercingQuery(int x)
{
//从ML中查找区间
if(x <= xMed)
{
for(vector::iterator i = mL.begin(); i < mL.end(); ++i)
{
if(x < i->l)
{
break;
}
cout<<*(i->parent);
}
}
//从MR中查找区间
if(x > xMed)
{
for(vector::iterator i = mR.begin(); i < mR.end(); ++i)
{
if(x > i->r)
{
break;
}
cout<<*(i->parent);
}
}
//从左右子树中递归查找区间
if(lTree)
lTree->PiercingQuery(x);
if(rTree)
rTree->PiercingQuery(x);
}
