基于Problem Solving with Algorithms and Data Structures using Python的学习记录(3)——Basic Data Structures
3.1.目标
● 了解抽象数据类型:栈 stack、队列 queue、双端队列 deque 和列表 list;
● 用 Python 列表数据结构,来实现 stack/queue/deque 抽象数据类型的构建;
● 了解各种基本线性数据结构的性能和使用方法;
● 了解前缀、中缀和后缀表达式;
● 采用栈 stack 对后缀表达式进行求值;
● 采用栈 stack 将中缀表达式转换为后缀表达式;
● 采用队列 queue 进行基本的时间模拟;
● 能够明确问题类型,选用 stack、queue 或者 deque 中合适的数据结构;
● 能够采用节点和引用模式来将抽象数据类型 list 实现为链表;,
● 能够比较链表和列表的算法性能。
3.2 什么是线性结构?
在我们开始数据结构的学习之前,先来看看四个简单但非常强大的概念: 栈,队列,双端队列,和列表。这四种数据集合的项的由添加或删除的方式整合在一起。当添加一个项目时,它就被放在这样一个位置:在之前存在的项与后来要加入的项之间。像这样的数据集合常被称为线性数据结构。
你可以想象线性结构有两个端,有时候,我们称这两端为“左”和“右”,或者“前”和“后”,或者“顶”和“底”。其实名字不重要,区别线性结构和其他结构的依据是项进行添加和删除的方式,尤其是添加和删除发生的位置。例如,有的结构可能仅允许仅在一端加项;有的结构可能会允许从两端移除项。
3.3.什么是栈
栈(有时称为“后进先出栈”)是一个项的有序集合,其中添加移除新项总发生在同一端。这一端通常称为“顶部”。与顶部对应的端称为“底部”。
栈的底部很重要,因为在栈中靠近底部的项是存储时间最长的。最近添加的项是最先会被移除的。这种排序原则有时被称为 LIFO(last-in first-out),后进先出。它基于在集合内的时间长度做排序。较新的项靠近顶部,较旧的项靠近底部。
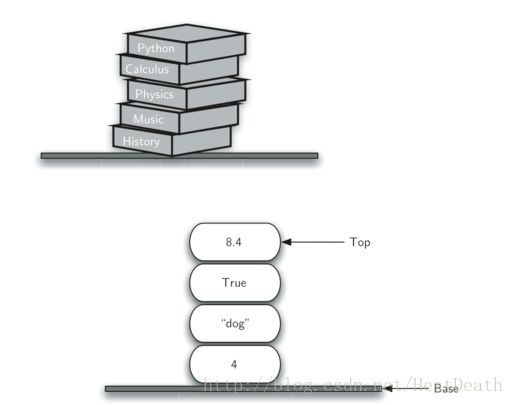
栈的例子很常见。几乎所有的自助餐厅都有一堆托盘或盘子,你从顶部拿一个,就会有一个新的托盘给下一个客人。想象桌上有一堆书(Figure 1), 只有顶部的那本书封面可见,要看到其他书的封面,只有先移除他们上面的书。Figure 2 展示了另一个栈,包含了很多 Python 对象。
和栈相关的最有用的想法之一来自对它的观察。假设从一个干净的桌面开始,现在把书一本本叠起来,你在构造一个栈。考虑下移除一本书会发生什么。移除的顺序跟刚刚被放置的顺序相反。栈之所以重要是因为它能反转项的顺序。插入跟删除顺序相反,Figure 3 展示了 Python 数据对象创建和删除的过程,注意观察他们的顺序。
想想这种反转的属性,你可以想到使用计算机的时候所碰到的例子。例如,每个 web 浏览器都有一个返回按钮。当你浏览网页时,这些网页被放置在一个栈中(实际是网页的网址)。你现在查看的网页在顶部,你第一个查看的网页在底部。如果按‘返回’按钮,将按相反的顺序浏览刚才的页面。
3.4.栈的抽象数据类型
栈的抽象数据类型由以下结构和操作定义。如上所述,栈被构造为项的有序集合,其中项被添加和从末端移除的位置称为“顶部”。栈是有序的 LIFO 。栈操作如下。
- Stack() 创建一个空的新栈。 它不需要参数,并返回一个空栈。
- push(item)将一个新项添加到栈的顶部。它需要 item 做参数并不返回任何内容。
- pop() 从栈中删除顶部项。它不需要参数并返回 item 。栈被修改。
- peek() 从栈返回顶部项,但不会删除它。不需要参数。 不修改栈。
- isEmpty() 测试栈是否为空。不需要参数,并返回布尔值。
- size() 返回栈中的 item 数量。不需要参数,并返回一个整数。
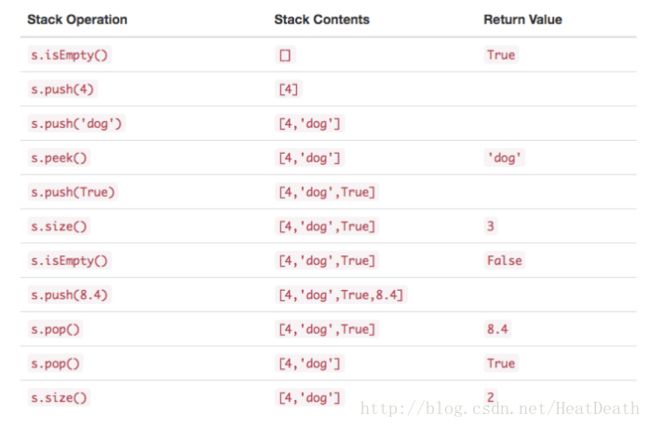
例如,s 是已经创建的空栈,Table1 展示了栈操作序列的结果。栈中,顶部项列在最右边。
3.5.Python实现栈
现在我们已经将栈清楚地定义了抽象数据类型,我们将把注意力转向使用 Python 实现栈。回想一下,当我们给抽象数据类型一个物理实现时,我们将实现称为数据结构。
正如我们在第1章中所描述的,在 Python 中,与任何面向对象编程语言一样,抽象数据类型(如栈)的选择的实现是创建一个新类。栈操作实现为类的方法。此外,为了实现作为元素集合的栈,使用由 Python 提供的原语集合的能力是有意义的。 我们将使用列表作为底层实现。
回想一下,Python 中的列表类提供了有序集合机制和一组方法。例如,如果我们有列表 [2,5,3,6,7,4],我们只需要确定列表的哪一端将被认为是栈的顶部。一旦确定,可以使用诸如 append 和 pop 的列表方法来实现操作。
以下栈实现(ActiveCode 1)假定列表的结尾将保存栈的顶部元素。随着栈增长(push 操作),新项将被添加到列表的末尾。 pop 也操作列表末尾的元素。
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self,item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)记住我们只定义类的实现,我们需要创建一个栈,然后使用它。ActiveCode 2 展示了我们通过实例化 Stack 类执行 Table 1中的操作。注意,Stack 类的定义是从 pythonds 模块导入的。
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self,item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
if __name__ =='__main__':
s=Stack()
print(s)
print("Stack是否为空:",s.isEmpty())
s.push(4)
s.push('dog')
print("栈顶元素是:",s.peek())
s.push(True)
print("栈的长度是:",s.size())
print("出栈元素:",s.pop())
print("出栈元素:", s.pop())
print("栈的长度是:", s.size())
3.6.简单括号匹配
区分括号是否匹配的能力是识别很多编程语言结构的重要部分。具有挑战的是如何编写一个算法,能够从左到右读取一串符号,并决定符号是否平衡。为了解决这个问题,我们需要做一个重要的观察。从左到右处理符号时,最近开始符号必须与下一个关闭符号相匹配(见 Figure 4)。此外,处理的第一个开始符号必须等待直到其匹配最后一个符号。结束符号以相反的顺序匹配开始符号。他们从内到外匹配。这是一个可以用栈解决问题的线索。
一旦你认为栈是保存括号的恰当的数据结构,算法是很直接的。从空栈开始,从左到右处理括号字符串。如果一个符号是一个开始符号,将其作为一个信号,对应的结束符号稍后会出现。另一方面,如果符号是结束符号,弹出栈,只要弹出栈的开始符号可以匹配每个结束符号,则括号保持匹配状态。如果任何时候栈上没有出现符合开始符号的结束符号,则字符串不匹配。最后,当所有符号都被处理后,栈应该是空的。实现此算法的 Python 代码见 ActiveCode 1。
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self,item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
'''
读取输入的只包含"("和")"的符号串
如果是"("则入栈
如果是")"则先检查栈是否为空,如果为空,则Not balance,否则pop()栈顶的"("
当遍历了符号串中的所有元素后,如果栈为空,且balance,则括号匹配;否则,不匹配
'''
def parChecker(symbolString):
s = Stack()
balanced = True
index = 0
while index < len(symbolString) and balanced:
symbol = symbolString[index]
if symbol == "(":
s.push(symbol)
else:
if s.isEmpty():
balanced = False
else:
s.pop()
index = index + 1
if balanced and s.isEmpty():
return True
else:
return False
print(parChecker('((()))'))
print(parChecker('(()'))
3.7.符号匹配
上面显示的匹配括号问题是许多编程语言都会出现的一般情况的特定情况。匹配和嵌套不同种类的开始和结束符号的情况经常发生。例如,在 Python 中,方括号 [ 和 ] 用于列表,花括号 { 和 } 用于字典。括号 ( 和 ) 用于元祖和算术表达式。只要每个符号都能保持自己的开始和结束关系,就可以混合符号。
回想一下,每个开始符号被简单的压入栈中,等待匹配的结束符号出现。当出现结束符号时,唯一的区别是我们必须检查确保它正确匹配栈顶部开始符号的类型。如果两个符号不匹配,则字符串不匹配。如果整个字符串都被处理完并且没有什么留在栈中,则字符串匹配。
Python 程序见 ActiveCode 1。唯一的变化是 16 行,我们称之为辅助函数匹配。必须检查栈中每个删除的符号,以查看它是否与当前结束符号匹配。如果不匹配,则布尔变量 balanced 被设置为 False。
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self,item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
'''
读取输入的只包含"([{"和")]}"的符号串
如果是"([{"则入栈
如果是")]}"则先检查栈是否为空,如果为空,则Not balance,否则pop()栈顶的"([{",
运行辅助匹配函数,如果不匹配,则Not balande。当遍历了符号串中的所有元素后,如果栈为空,
且balance,则符号匹配;否则,不匹配
'''
def parChecker(symbolString):
s = Stack()
balanced = True
index = 0
while index < len(symbolString) and balanced:
symbol = symbolString[index]
if symbol in "([{":
s.push(symbol)
else:
if s.isEmpty():
balanced = False
else:
top = s.pop()
if not matches(top,symbol):
balanced = False
index = index + 1
if balanced and s.isEmpty():
return True
else:
return False
def matches(open,close):
opens = "([{"
closers = ")]}"
return opens.index(open) == closers.index(close)
print(parChecker('{{([][])}()}'))
print(parChecker('[{()]'))
3.8.十进制转换成二进制
们如何能够容易地将整数值转换为二进制呢?答案是 “除 2”算法,它用栈来跟踪二进制结果的数字。
“除 2” 算法假定我们从大于 0 的整数开始。不断迭代的将十进制除以 2,并跟踪余数。第一个除以 2 的余数说明了这个值是偶数还是奇数。偶数有 0 的余数,记为 0。奇数有余数 1,记为 1.我们将得到的二进制构建为数字序列,第一个余数实际上是序列中的最后一个数字。见 Figure 5 , 我们再次看到了反转的属性,表示栈可能是解决这个问题的数据结构。
Activecode 1 中的 Python 代码实现了 “除 2” 算法,函数 divideBy2 传入了一个十进制的参数,并重复除以 2。第 7 行使用内置的模运算符 % 来提取余数,第 8 行将余数压到栈上。当除到 0 后,11-13 行构造了一个二进制字符串。
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self,item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
def divideBy2(decNumber):
remstack = Stack()
while decNumber > 0:
rem = decNumber % 2
remstack.push(rem)
decNumber = decNumber // 2
binString =""
while not remstack.isEmpty():
binString = binString + str(remstack.pop())
return binString
print(divideBy2(42))可以修改 divideBy2 函数,使它不仅能接受十进制参数,还能接受预期转换的基数。‘除 2’ 的概念被简单的替换成更通用的 ‘除基数’。在 ActiveCode2 展示的是一个名为 baseConverter 函数。采用十进制数和 2 到 16 之间的任何基数作为参数。余数部分仍然入栈,直到被转换的值为 0。我们创建一组数字,用来表示超过 9 的余数。
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self,item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
def baseConverter(decNumber,base):
remstack = Stack()
while decNumber > 0:
rem = decNumber % base
remstack.push(rem)
decNumber = decNumber // base
binString =""
digits = '0123456789ABCDEF'
while not remstack.isEmpty():
binString = binString + digits[remstack.pop()]
return binString
print(baseConverter(42,16))
print(baseConverter(47,8))3.9.中缀前缀和后缀表达式
看到这个突然想起了离散数学里学的波兰表达式和逆波兰表达式,啊,先学下一节吧
3.10.什么是队列
队列是项的有序结合,其中添加新项的一端称为队尾,移除项的一端称为队首。当一个元素从队尾进入队列时,一直向队首移动,直到它成为下一个需要移除的元素为止。
最近添加的元素必须在队尾等待。集合中存活时间最长的元素在队首,这种排序成为 FIFO,先进先出,也被成为先到先得。
3.11.队列抽象数据类型
队列抽象数据类型由以下结构和操作定义。如上所述,队列被构造为在队尾添加项的有序集合,并且从队首移除。队列保持 FIFO 排序属性。 队列操作如下。
- Queue() 创建一个空的新队列。 它不需要参数,并返回一个空队列。
- enqueue(item) 将新项添加到队尾。 它需要 item 作为参数,并不返回任何内容。
- dequeue() 从队首移除项。它不需要参数并返回 item。 队列被修改。
- isEmpty() 查看队列是否为空。它不需要参数,并返回布尔值。
- size() 返回队列中的项数。它不需要参数,并返回一个整数。
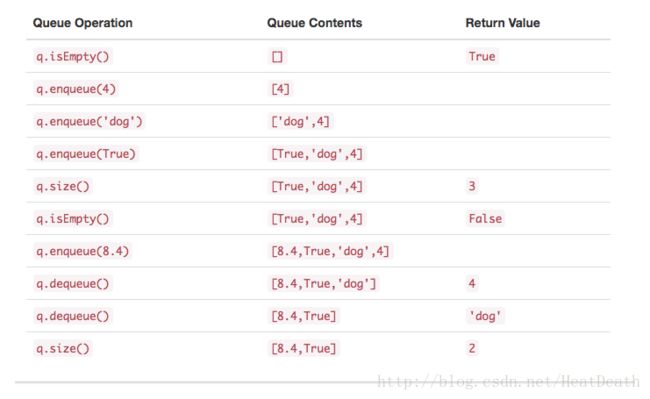
作为示例,我们假设 q 是已经创建并且当前为空的队列,则 Table 1 展示了队列操作序列的结果。右边表示队首。 4 是第一个入队的项,因此它 dequeue 返回的第一个项。
3.12.Python实现队列
我们将使用列表集合来作为构建队列的内部表示。
我们需要确定列表的哪一端作为队首,哪一端作为队尾。Listing 1 所示的实现假定队尾在列表中的位置为 0。这允许我们使用列表上的插入函数向队尾添加新元素。弹出操作可用于删除队首的元素(列表的最后一个元素)。回想一下,这也意味着入队为 O(n),出队为 O(1)。
class Queue:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def enqueue(self,item):
self.items.insert(0,item)
def dequeue(self):
return self.items.pop()
def size(self):
return len(self.items)
q = Queue()
q.enqueue(4)
q.enqueue('dog')
q.enqueue(True)
#list左侧是队尾,右侧是队首
print(q.size())
print(q.items)
print(q.isEmpty())
print(q.dequeue())
print(q.dequeue())3.13.约瑟夫的裁决之剑
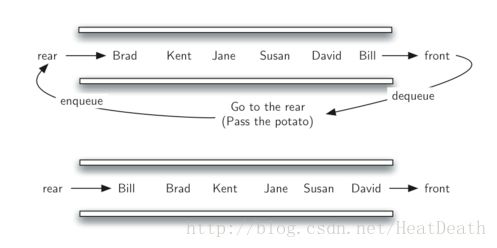
队列的典型应用之一是模拟需要以 FIFO 方式管理数据的真实场景。
这个游戏相当于著名的约瑟夫问题,一个一世纪著名历史学家弗拉维奥·约瑟夫斯的传奇故事。故事讲的是,他和他的 39 个战友被罗马军队包围在洞中。他们决定宁愿死,也不成为罗马人的奴隶。他们围成一个圈,其中一人被指定为第一个人,顺时针报数到第七人,就将他杀死。约瑟夫斯是一个成功的数学家,他立即想出了应该坐到哪才能成为最后一人。
class Queue:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def enqueue(self,item):
self.items.insert(0,item)
def dequeue(self):
return self.items.pop()
def size(self):
return len(self.items)
def hotPotato(namelist,num):
simqueue = Queue()
for name in namelist:
simqueue.enqueue(name)
#当幸存人数>1时,这个过程持续下去
while simqueue.size() > 1:
#模拟报数过程,队首的人即为被裁决之剑指向人
#约瑟夫环的裁决之剑持续转动,当约瑟夫环的裁决之剑停止转动时,被指向的那个狗带
for i in range(num):
#约瑟夫环的裁决之剑转动了一个单位
simqueue.enqueue(simqueue.dequeue())
#约瑟夫环中狗带的人
simqueue.dequeue()
#约瑟夫环最后幸存的人的名字
return simqueue.dequeue()
print(hotPotato(["Biu~","David","Susan","Jane","Kent","Brad"],7))3.14.模拟:打印机
平均每天大约10名学生在任何给定时间在实验室工作。这些学生通常在此期间打印两次,这些任务的长度范围从1到20页。实验室中的打印机较旧,每分钟以草稿质量可以处理10页。打印机可以切换以提供更好的质量,但是它将每分钟只能处理五页。较慢的打印速度可能会使学生等待太久。应使用什么页面速率?
我们可以通过建立一个模拟实验来决定。我们将需要为学生,打印任务和打印机构建表现表示(Figure 4)。当学生提交打印任务时,我们将把他们添加到等待列表中,一个打印任务的队列。 当打印机完成任务时,它将检查队列,以检查是否有剩余的任务要处理。我们感兴趣的是学生等待他们的论文打印的平均时间。这等于任务在队列中等待的平均时间量。
为了为这种情况建模,我们需要使用一些概率。例如,学生可以打印长度从 1 到 20 页的纸张。如果从 1 到 20 的每个长度有同样的可能性,则可以通过使用 1 和 20 之间的随机数来模拟打印任务的实际长度。这意味着出现从 1 到 20 的任何长度的机会是平等的。
如果实验室中有 10 个学生,每人打印两次,则平均每小时有 20 个打印任务。 在任何给定的秒,打印任务将被创建的机会是什么? 回答这个问题的方法是考虑任务与时间的比率。每小时 20 个任务意味着平均每 180 秒将有一个任务:

对于每一秒,我们可以通过生成 1 到 180 之间的随机数来模拟打印任务发生的机会。如果数字是 180,我们说一个任务已经创建。请注意,可能会在一下子创建许多任务,或者需要等待一段时间才有任务。这就是模拟的本质。你想模拟真实的情况就需要尽可能接近一般参数。
3.14.1.主要模拟步骤
- 创建打印任务的队列,每个任务都有个时间戳。队列启动的时候为空。
- 每秒(currentSecond):
- 是否创建新的打印任务?如果是,将 currentSecond 作为时间戳添加到队列。
- 如果打印机不忙并且有任务在等待
-
- 从打印机队列中删除一个任务并将其分配给打印机
-
- 从 currentSecond 中减去时间戳,以计算该任务的等待时间。
-
- 将该任务的等待时间附件到列表中稍后处理。
-
- 根据打印任务的页数,确定需要多少时间。
- 打印机需要一秒打印,所以得从该任务的所需的等待时间减去一秒。
- 如果任务已经完成,换句话说,所需的时间已经达到零,打印机空闲。
- 模拟完成后,从生成的等待时间列表中计算平均等待时间。
3.14.2 Python 实现
为了设计此模拟,我们将为上述三个真实世界对象创建类:Printer, Task, PrintQueue
Printer 类(Listing 2)需要跟踪它当前是否有任务。如果有,则它处于忙碌状态(13-17 行),并且可以从任务的页数计算所需的时间。构造函数允许初始化每分钟页面的配置,tick 方法将内部定时器递减直到打印机设置为空闲(11 行)
class Printer():
def __init__(self,ppm):
self.pagerate = ppm
self.currentTask = None
self.timeRemaining = 0
#tick()方法将内部定时器递减直到打印机设置为空闲
def tick(self):
if self.currentTask != None:
self.timeRemaining = self.timeRemaining - 1
if self.timeRemaining <= 0:
self.currentTask = None
#如果当前有任务,则打印机处于忙碌状态
def busy(self):
if self.currentTask != None:
return True
else:
return False
#从任务页数计算所需要的时间
def startNext(self,newtask):
self.currentTask = newtask
self.timeRemaining = newtask.getPages() * 60 / self.pagerate
Task 类(Listing 3)表示单个打印任务。创建任务时,随机数生成器将提供 1 到 20 页的长度。我们选择使用随机模块中的 randrange 函数。
每个任务还需要保存一个时间戳用于计算等待时间。此时间戳将表示任务被创建并放置到打印机队列中的时间。可以使用 waitTime 方法来检索在打印开始之前队列中花费的时间。
import random
class Printer:
def __init__(self,ppm):
self.pagerate = ppm
self.currentTask = None
self.timeRemaining = 0
#tick()方法将内部定时器递减直到打印机设置为空闲
def tick(self):
if self.currentTask != None:
self.timeRemaining = self.timeRemaining - 1
if self.timeRemaining <= 0:
self.currentTask = None
#如果当前有任务,则打印机处于忙碌状态
def busy(self):
if self.currentTask != None:
return True
else:
return False
#从任务页数计算所需要的时间
def startNext(self,newtask):
self.currentTask = newtask
self.timeRemaining = newtask.getPages() * 60 / self.pagerate
class Task:
def __init__(self,time):
self.timestamp = time
self.pages = random.randrange(1,21)
#此时间戳将表示任务被创建并放置到打印机队列中的时间。
def getStamp(self):
return self.timestamp
#随机数生成器将提供 1 到 20 页的长度
def getPages(self):
return self.pages
#使用 waitTime() 方法来检索在打印开始之前队列中花费的时间。
def waitTime(self, currenttime):
return currenttime - self.timestamp
class Queue:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def enqueue(self,item):
self.items.insert(0,item)
def dequeue(self):
return self.items.pop()
def size(self):
return len(self.items)
#模拟功能允许我们设置打印机的总时间和每分钟的页数
def simulation(numSeconds, pagesPerMinute):
labprinter = Printer(pagesPerMinute)
# PrintQueue 对象是我们现有队列 ADT 的一个实例
printQueue = Queue()
waitingtimes = []
for currentSecond in range(numSeconds):
if newPrintTask():
task = Task(currentSecond)
printQueue.enqueue(task)
if (not labprinter.busy()) and (not printQueue.isEmpty()):
nexttask = printQueue.dequeue()
waitingtimes.append(nexttask.waitTime(currentSecond))
labprinter.startNext(nexttask)
labprinter.tick()
averageWait = sum(waitingtimes)/len(waitingtimes)
print("Average Wait %6.2f secs %3d tasks remaining."%(averageWait,printQueue.size()))
#newPrintTask 决定是否创建一个新的打印任务
def newPrintTask():
num = random.randrange(1,181)
if num == 180:
return True
else:
False
#我们将使用每分钟五页的页面速率运行模拟 60 分钟(3,600秒)
#此外,我们将进行 10 次独立试验。
for i in range(10):
simulation(3600, 5)
当我们运行模拟时,我们不应该担心每次的结果不同。这是由于随机数的概率性质决定的。 因为模拟的参数可以被调整,我们对调整后可能发生的趋势感兴趣。 这里有一些结果。
首先,我们将使用每分钟五页的页面速率运行模拟 60 分钟(3,600秒)。 此外,我们将进行 10 次独立试验。记住,因为模拟使用随机数,每次运行将返回不同的结果。
>>>for i in range(10):
simulation(3600,5)
Average Wait 165.38 secs 2 tasks remaining.
Average Wait 95.07 secs 1 tasks remaining.
Average Wait 65.05 secs 2 tasks remaining.
Average Wait 99.74 secs 1 tasks remaining.
Average Wait 17.27 secs 0 tasks remaining.
Average Wait 239.61 secs 5 tasks remaining.
Average Wait 75.11 secs 1 tasks remaining.
Average Wait 48.33 secs 0 tasks remaining.
Average Wait 39.31 secs 3 tasks remaining.
Average Wait 376.05 secs 1 tasks remaining.在运行 10 次实验后,我们可以看到,平均等待时间为 122.09 秒。 还可以看到平均等待时间有很大的变化,最小值为 17.27 秒,最大值为 376.05 秒。 你也可能注意到,只有两种情况所有任务都完成。
现在,我们将页面速率调整为每分钟 10 页,再次运行 10 次测试,页面速度更快,我们希望在一小时内完成更多的任务。
>>>for i in range(10):
simulation(3600,10)
Average Wait 1.29 secs 0 tasks remaining.
Average Wait 7.00 secs 0 tasks remaining.
Average Wait 28.96 secs 1 tasks remaining.
Average Wait 13.55 secs 0 tasks remaining.
Average Wait 12.67 secs 0 tasks remaining.
Average Wait 6.46 secs 0 tasks remaining.
Average Wait 22.33 secs 0 tasks remaining.
Average Wait 12.39 secs 0 tasks remaining.
Average Wait 7.27 secs 0 tasks remaining.
Average Wait 18.17 secs 0 tasks remaining.3.14.3.讨论
我们试图回答一个问题,即当前打印机是否可以处理任务负载,如果它设置为打印更好的质量,较慢的页面速率。我们采用的方法是编写一个模拟打印任务作为各种页数和到达时间的随机事件的模拟。
上面的输出显示,每分钟打印 5 页,平均等待时间从低的 17 秒到高的 376 秒(约 6 分钟)。使用更快的打印速率,低值为 1 秒,高值仅为 28。此外,在 10 次运行中的 8 次,每分钟 5 页,打印任务在结束时仍在队列中等待。
因此,我们说减慢打印机的速度以获得更好的质量可能不是一个好主意。学生们不能等待他们的论文打印完,特别是当他们需要到下一个班级。六分钟的等待时间太长了。
这种类型的模拟分析允许我们回答许多问题,通常被称为“如果”的问题。我们需要做的是改变模拟使用的参数,我们可以模拟任何数量。
3.15.什么是Deque
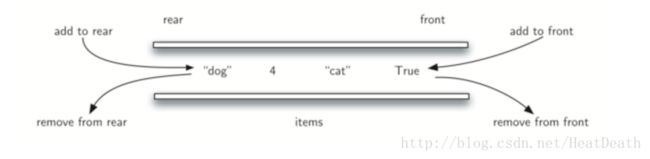
deque(也称为双端队列)是与队列类似的项的有序集合。它有两个端部,首部和尾部,并且项在集合中保持不变。deque 不同的地方是添加和删除项是非限制性的。可以在前面或后面添加新项。同样,可以从任一端移除现有项。在某种意义上,这种混合线性结构提供了单个数据结构中的栈和队列的所有能力。 Figure 1 展示了一个 Python 数据对象的 deque 。
要注意,即使 deque 可以拥有栈和队列的许多特性,它不需要由那些数据结构强制的 LIFO 和 FIFO 排序。这取决于你如何持续添加和删除操作。
3.16.Deque抽象数据类型
deque 抽象数据类型由以下结构和操作定义。如上所述,deque 被构造为项的有序集合,其中项从首部或尾部的任一端添加和移除。下面给出了 deque 操作。
Deque() 创建一个空的新 deque。它不需要参数,并返回空的 deque。
- addFront(item) 将一个新项添加到 deque 的首部。它需要 item 参数 并不返回任何内容。
- addRear(item) 将一个新项添加到 deque 的尾部。它需要 item 参数并不返回任何内容。
- removeFront() 从 deque 中删除首项。它不需要参数并返回 item。deque 被修改。
- removeRear() 从 deque 中删除尾项。它不需要参数并返回 item。deque 被修改。
- isEmpty() 测试 deque 是否为空。它不需要参数,并返回布尔值。
- size() 返回 deque 中的项数。它不需要参数,并返回一个整数。
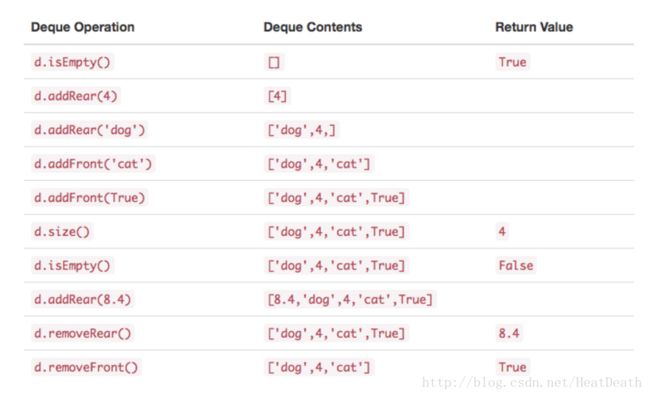
例如,我们假设 d 是已经创建并且当前为空的 deque,则 Table 1 展示了一系列 deque 操作的结果。注意,首部的内容列在右边。在将 item 移入和移出时,跟踪前面和后面是非常重要的,因为可能会有点混乱。
3.17.Python实现Deque
正如我们在前面的部分中所做的,我们将为抽象数据类型 deque 的实现创建一个新类。同样,Python 列表将提供一组非常好的方法来构建 deque 的细节。我们的实现(Listing 1)将假定 deque 的尾部在列表中的位置为 0。
'''
Deque() 创建一个空的新 deque。它不需要参数,并返回空的 deque。
addFront(item) 将一个新项添加到 deque 的首部。它需要 item 参数 并不返回任何内容。
addRear(item) 将一个新项添加到 deque 的尾部。它需要 item 参数并不返回任何内容。
removeFront() 从 deque 中删除首项。它不需要参数并返回 item。deque 被修改。
removeRear() 从 deque 中删除尾项。它不需要参数并返回 item。deque 被修改。
isEmpty() 测试 deque 是否为空。它不需要参数,并返回布尔值。
size() 返回 deque 中的项数。它不需要参数,并返回一个整数。
'''
class Deque:
def __init__(self):
self.items = []
def addFront(self,item):
self.items.append(item)
def addRear(self,item):
self.items.insert(0,item)
def removeFront(self):
return self.items.pop()
def removerRear(self):
return self.items.pop(0)
def isEmpty(self):
return self.items == []
def size(self):
return len(self.items)
在 removeFront 中,我们使用 pop 方法从列表中删除最后一个元素。 但是,在removeRear中,pop(0)方法必须删除列表的第一个元素。同样,我们需要在 addRear 中使用insert方法(第12行),因为 append 方法在列表的末尾添加一个新元素。
你可以看到许多与栈和队列中描述的 Python 代码相似之处。你也可能观察到,在这个实现中,从前面添加和删除项是 O(1),而从后面添加和删除是 O(n)。 考虑到添加和删除项是出现的常见操作,这是可预期的。 同样,重要的是要确定我们知道在实现中前后都分配在哪里。
3.18.回文检查
使用 deque 数据结构可以容易地解决经典回文问题。回文是一个字符串,读取首尾相同的字符,例如,radar toot madam。 我们想构造一个算法输入一个字符串,并检查它是否是一个回文。
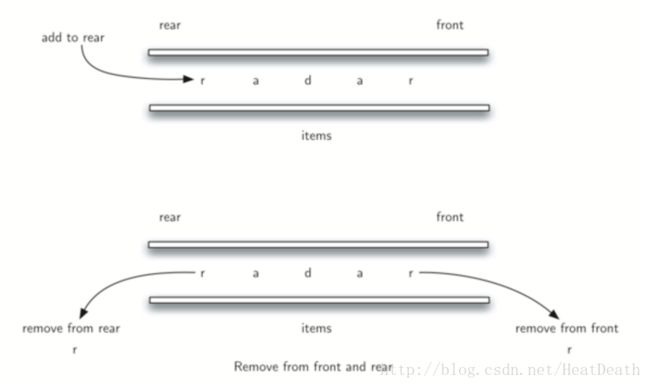
该问题的解决方案将使用 deque 来存储字符串的字符。我们从左到右处理字符串,并将每个字符添加到 deque 的尾部。在这一点上,deque 像一个普通的队列。然而,我们现在可以利用 deque 的双重功能。 deque 的首部保存字符串的第一个字符,deque 的尾部保存最后一个字符(见 Figure 2)。
我们可以直接删除并比较首尾字符,只有当它们匹配时才继续。如果可以持续匹配首尾字符,我们最终要么用完字符,要么留出大小为 1 的deque,取决于原始字符串的长度是偶数还是奇数。在任一情况下,字符串都是回文。 回文检查的完整功能在 ActiveCode 1 中。
class Deque:
def __init__(self):
self.items = []
def addFront(self,item):
self.items.append(item)
def addRear(self,item):
self.items.insert(0,item)
def removeFront(self):
return self.items.pop()
def removeRear(self):
return self.items.pop(0)
def isEmpty(self):
return self.items == []
def size(self):
return len(self.items)
def palchecker(aString):
chardeque = Deque()
for ch in aString:
chardeque.addRear(ch)
stillEqual = True
while chardeque.size() > 1 and stillEqual:
first = chardeque.removeFront()
last = chardeque.removeRear()
if first != last:
stillEqual = False
return stillEqual
print(palchecker("lsdkjfskf"))
print(palchecker("radar"))3.19.列表
在对基本数据结构的讨论中,我们使用 Python 列表来实现所呈现的抽象数据类型。列表是一个强大但简单的收集机制,为程序员提供了各种各样的操作。然而,不是所有的编程语言都包括列表集合。在这些情况下,列表的概念必须由程序员实现。
列表是项的集合,其中每个项保持相对于其他项的相对位置。更具体地,我们将这种类型的列表称为无序列表。我们可以将列表视为具有第一项,第二项,第三项等等。我们还可以引用列表的开头(第一个项)或列表的结尾(最后一个项)。为了简单起见,我们假设列表不能包含重复项。
例如,整数 54,26,93,17,77 和 31 的集合可以表示考试分数的简单无序列表。请注意,我们将它们用逗号分隔,这是列表结构的常用方式。当然,Python 会显示这个列表为 [54,26,93,17,77,31]。
3.20.无序列表抽象数据类型
如上所述,无序列表的结构是项的集合,其中每个项保持相对于其他项的相对位置。下面给出了一些可能的无序列表操作。
- List() 创建一个新的空列表。它不需要参数,并返回一个空列表。
- add(item) 向列表中添加一个新项。它需要 item 作为参数,并不返回任何内容。假定该 item 不在列表中。
- remove(item) 从列表中删除该项。它需要 item 作为参数并修改列表。假设项存在于列表中。
- search(item) 搜索列表中的项目。它需要 item 作为参数,并返回一个布尔值。
- size()返回列表中的项数。它不需要参数,并返回一个整数。
- append(item) 将一个新项添加到列表的末尾,使其成为集合中的最后一项。它需要 item 作为参数,并不返回任何内容。假定该项不在列表中。
- index(item) 返回项在列表中的位置。它需要 item 作为参数并返回索引。假定该项在列表中。
- insert(pos,item) 在位置 pos 处向列表中添加一个新项。它需要 item
作为参数并不返回任何内容。假设该项不在列表中,并且有足够的现有项使其有 pos 的位置。 - pop() 删除并返回列表中的最后一个项。假设该列表至少有一个项。
- pop(pos) 删除并返回位置 pos 处的项。它需要 pos 作为参数并返回项。假定该项在列表中。
3.21.实现无序列表:链表
为了实现无序列表,我们将构造通常所知的链表。回想一下,我们需要确保我们可以保持项的相对定位。然而,没有要求我们维持在连续存储器中的定位。例如,考虑 Figure 1 中所示的项的集合。看来这些值已被随机放置。如果我们可以在每个项中保持一些明确的信息,即下一个项的位置(参见 Figure 2),则每个项的相对位置可以通过简单地从一个项到下一个项的链接来表示。
要注意,必须明确地指定链表的第一项的位置。一旦我们知道第一个项在哪里,第一个项目可以告诉我们第二个是什么,等等。外部引用通常被称为链表的头。类似地,最后一个项需要知道没有下一个项。
3.21.1.Node 类
链表实现的基本构造块是节点。每个节点对象必须至少保存两个信息。首先,节点必须包含列表项本身。我们将这个称为节点的数据字段。此外,每个节点必须保存对下一个节点的引用。 Listing 1 展示了 Python 实现。要构造一个节点,需要提供该节点的初始数据值。下面的赋值语句将产生一个包含值 93 的节点对象(见 Figure 3)。应该注意,我们通常会如 Figure 4 所示表示一个节点对象。Node 类还包括访问,修改数据和访问下一个引用的常用方法。
class Node:
def __init__(self, initdata):
self.data = initdata
self.next = None
def getData(self):
return self.data
def getNext(self):
return self.next
def setData(self,newdata):
self.data = newdata
def setNext(self,newnext):
self.next = newnext
Python 引用值 None 将在 Node 类和链表本身发挥重要作用。引用 None 代表没有下一个节点。请注意在构造函数中,最初创建的节点 next 被设置为 None。有时这被称为 接地节点,因此我们使用标准接地符号表示对 None 的引用。将 None 显式的分配给初始下一个引用值是个好主意。
3.21.2.Unordered List 类
如上所述,无序列表将从一组节点构建,每个节点通过显式引用链接到下一个节点。只要我们知道在哪里找到第一个节点(包含第一个项),之后的每个项可以通过连续跟随下一个链接找到。考虑到这一点,UnorderedList 类必须保持对第一个节点的引用。Listing 2 显示了构造函数。注意,每个链表对象将维护对链表头部的单个引用。
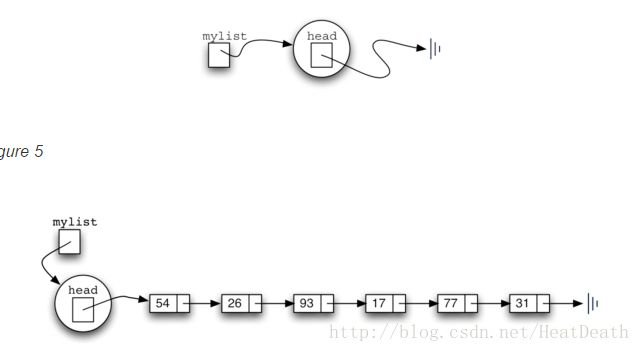
创建如 Figure 5 所示的链表。正如我们在 Node 类中讨论的,特殊引用 None 将再次用于表示链表的头部不引用任何内容。最终,先前给出的示例列表如 Figure 6 所示的链接列表表示。链表的头指代列表的第一项的第一节点。反过来,该节点保存对下一个节点(下一个项)的引用,等等。重要的是注意链表类本身不包含任何节点对象。相反,它只包含对链接结构中第一个节点的单个引用。
Listing 3 中所示的 isEmpty 方法只是检查链表头是否是 None 的引用。 布尔表达式 self.head == None 的结果只有在链表中没有节点时才为真。由于新链表为空,因此构造函数和空检查必须彼此一致。这显示了使用引用 None 来表示链接结构的 end 的优点。在 Python 中,None 可以与任何引用进行比较。如果它们都指向相同的对象,则两个引用是相等的。我们将在其他方法中经常使用它。
那么,我们如何将项加入我们的链表?我们需要实现 add 方法。然而,在我们做这一点之前,我们需要解决在链表中哪个位置放置新项的重要问题。由于该链表是无序的,所以新项相对于已经在列表中的其他项的特定位置并不重要。 新项可以在任何位置。考虑到这一点,将新项放在最简单的位置是有意义的。
回想一下,链表结构只为我们提供了一个入口点,即链表的头部。所有其他节点只能通过访问第一个节点,然后跟随下一个链接到达。这意味着添加新节点的最简单的地方就在链表的头部。 换句话说,我们将新项作为链表的第一项,现有项将需要链接到这个新项后。
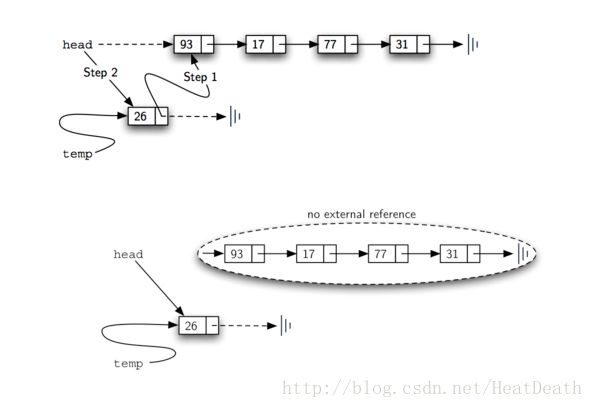
add 方法如 Listing 4 所示。链表的每项必须驻留在节点对象中。第 2 行创建一个新节点并将该项作为其数据。现在我们必须通过将新节点链接到现有结构中来完成该过程。这需要两个步骤,如 Figure 7 所示。步骤1(行3)更改新节点的下一个引用以引用旧链表的第一个节点。现在,链表的其余部分已经正确地附加到新节点,我们可以修改链表的头以引用新节点。第 4 行中的赋值语句设置列表的头。
上述两个步骤的顺序非常重要。如果第 3 行和第 4 行的顺序颠倒,会发生什么?如果链表头部的修改首先发生,则结果可以在 Figure 8 中看到。由于 head 是链表节点的唯一外部引用,所有原始节点都将丢失并且不能再被访问。
def add(self,item):
temp = Node(item)
temp.setNext(self.head)
self.head = temp我们将实现的下面的方法 - size,search 和 remove - 都基于一种称为链表遍历的技术。遍历是指系统地访问每个节点的过程。为此,我们使用从链表中第一个节点开始的外部引用。当我们访问每个节点时,我们通过“遍历”下一个引用来移动到对下一个节点的引用。
要实现 size 方法,我们需要遍历链表并对节点数计数。Listing 5 展示了用于计算列表中节点数的 Python 代码。外部引用称为 current,并在第二行被初始化到链表的头部。开始的时候,我们没有看到任何节点,所以计数设置为 0 。第 4-6 行实际上实现了遍历。只要当前引用没到链表的结束位置(None),我们通过第 6 行中的赋值语句将当前元素移动到下一个节点。再次,将引用与 None 进行比较的能力是非常有用的。每当 current 移动到一个新的节点,我们加 1 以计数。最后,count 在迭代停止后返回。Figure 9 展示了处理这个链表的过程。
def size(self):
current = self.head
count = 0
while current != None:
count = count + 1
current = current.getNext()
return count在链表中搜索也使用遍历技术。当我们访问链表中的每个节点时,我们将询问存储在其中的数据是否与我们正在寻找的项匹配。然而,在这种情况下,我们不必一直遍历到列表的末尾。事实上,如果我们到达链表的末尾,这意味着我们正在寻找的项不存在。此外,如果我们找到项,没有必要继续。
Listing 6 展示了搜索方法的实现。和在 size 方法中一样,遍历从列表的头部开始初始化(行2)。我们还使用一个布尔变量叫 found,标记我们是否找到了正在寻找的项。因为我们还没有在遍历开始时找到该项,found 设置为 False(第3行)。第4行中的迭代考虑了上述两个条件。只要有更多的节点访问,而且我们没有找到正在寻找的项,我们就继续检查下一个节点。第 5 行检查数据项是否存在于当前节点中。如果存在,found 设置为 True。
def search(self,item):
current = self.head
found = False
while current != None and not found:
if current.getData() == item:
found = True
else:
current = current.getNext()
return foundremove 方法需要两个逻辑步骤。首先,我们需要遍历列表寻找我们要删除的项。一旦我们找到该项(我们假设它存在),删除它。第一步非常类似于搜索。从设置到链表头部的外部引用开始,我们遍历链接,直到我们发现正在寻找的项。因为我们假设项存在,我们知道迭代将在 current 变为 None 之前停止。这意味着我们可以简单地使用 found 布尔值。
当 found 变为 True 时,current 将是对包含要删除的项的节点的引用。但是我们如何删除呢?一种方法是用标示该项目不再存在的某个标记来替换项目的值。这种方法的问题是节点数量将不再匹配项数量。最好通过删除整个节点来删除该项。
为了删除包含项的节点,我们需要修改上一个节点中的链接,以便它指向当前之后的节点。不幸的是,链表遍历没法回退。因为 current 指我们想要进行改变的节点之前的节点,所以进行修改太迟了。
这个困境的解决方案是在我们遍历链表时使用两个外部引用。current 将像之前一样工作,标记遍历的当前位置。新的引用,我们叫 previous,将总是传递 current后面的一个节点 。这样,当 current 停止在要被去除的节点时,previoud 将引用链表中用于修改的位置。
一旦 remove 的搜索步骤已经完成,我们需要从链表中删除该节点。 Figure 13 展示了要修改的链接。但是,有一个特殊情况需要解决。 如果要删除的项目恰好是链表中的第一个项,则 current 将引用链接列表中的第一个节点。这也意味着 previous 是 None。 我们先前说过,previous 是一个节点,它的下一个节点需要修改。在这种情况下,不是 previous ,而是链表的 head 需要改变
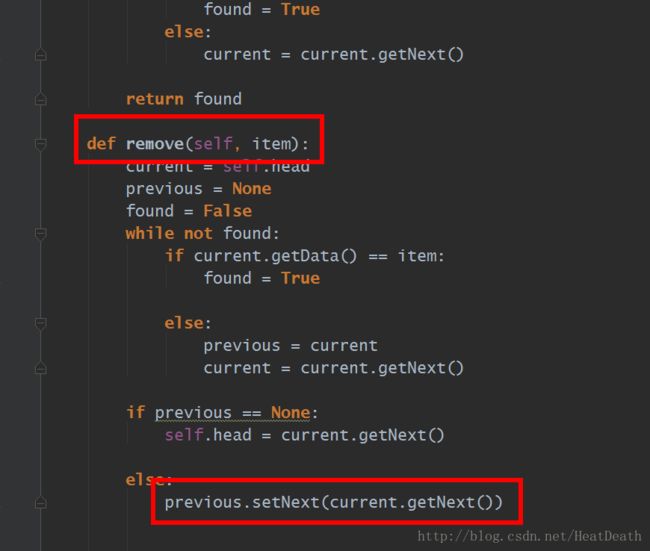
第 12 行检查是否处理上述的特殊情况。如果 previous 没有移动,当 found 的布尔变为 True 时,它仍是 None。 在这种情况下(行13),链表的 head 被修改以指代当前节点之后的节点,实际上是从链表中移除第一节点。 但是,如果 previous 不为 None,则要删除的节点位于链表结构的下方。 在这种情况下,previous 的引用为我们提供了下一个引用更改的节点。第 15 行使用之前的 setNext 方法完成删除。注意,在这两种情况下,引用更改的目标是 current.getNext()。 经常出现的一个问题是,这里给出的两种情况是否也将处理要移除的项在链表的最后节点中的情况。我们留给你思考。
思考
在设置Node的时候,已经将最后一个Node的next指针指向了None,所以当要删除的Node是链表中的最后一个Node的时候,当前设计的remove()方法可以处理这种情况
Check Yourself
- 剩下的方法append,insert,index,和pop留作练习。请记住,这些都必须考虑到更改是发生在列表的头部还是其他地方。此外,insert,index,并pop要求我们的名字列表的位置。我们假设位置名是以0开头的整数。
class Node:
def __init__(self, initdata):
self.data = initdata
self.next = None
def getData(self):
return self.data
def getNext(self):
return self.next
def setData(self,newdata):
self.data = newdata
def setNext(self,newnext):
self.next = newnext
class UnorderedList:
def __init__(self):
self.head = None
#isEmpty() 检查列表是否为空。它不需要参数,并返回布尔值。
def isEmpty(self):
return self.head == None
#add(item) 向列表中添加一个新项。它需要 item 作为参数,并不返回任何内容。假定该 item 不在列表中。
def add(self, item):
#链表的每项必须驻留在节点对象中
temp = Node(item)
#更改新节点的下一个引用以引用旧链表的第一个节点
temp.setNext(self.head)
#修改链表的头以引用新节点
self.head = temp
#size()返回列表中的项数。它不需要参数,并返回一个整数。
def size(self):
current = self.head
count = 0
while current != None:
count = count + 1
current = current.getNext()
return count
#search(item) 搜索列表中的项目。它需要 item 作为参数,并返回一个布尔值。
def search(self, item):
current = self.head
found = False
while current != None and not found:
if current.getData() == item:
found = True
else:
current = current.getNext()
return found
#remove(item) 从列表中删除该项。它需要 item 作为参数并修改列表。假设项存在于列表中。
def remove(self, item):
current = self.head
previous = None
found = False
while not found:
if current.getData() == item:
found = True
else:
previous = current
current = current.getNext()
if previous == None:
self.head = current.getNext()
else:
previous.setNext(current.getNext())
#append(item) 将一个新项添加到列表的末尾,使其成为集合中的最后一项。
#它需要 item 作为参数,并不返回任何内容。假定该项不在列表中
def append(self, item):
current = self.head
while current.getNext() != None:
current = current.getNext()
temp = Node(item)
current.setNext(temp)
#index(item) 返回项在列表中的位置。它需要 item 作为参数并返回索引。假定该项在列表中。
def index(self, item):
current = self.head
count = -1
found = False
while current != None and not found:
count = count + 1
if current.getData() == item:
found = True
else:
current = current.getNext()
if found:
return count
else:
return "Not found!"
#insert(pos,item) 在位置 pos 处向列表中添加一个新项。
#它需要 item 作为参数并不返回任何内容。假设该项不在列表中,并且有足够的现有项使其有 pos 的位置。
def insert(self, pos, item):
if pos > self.size() or pos < 0:
return "Out of index!"
current = self.head
count = 0
previous = None
temp = Node(item)
while current != None and count != pos:
count = count + 1
previous = current
current = current.getNext()
##处理头结点为最后一个节点的情况
if previous == None:
self.head = temp
temp.setNext(current)
#处理一般情况
else:
previous.setNext(temp)
temp.setNext(current)
#pop() 删除并返回列表中的最后一个项。假设该列表至少有一个项。
def pop_last(self):
current = self.head
previous = None
#遍历到游标current指向UnorderList的尾节点
while current.getNext() != None:
previous = current
current = current.getNext()
#处理头结点为尾节点的情况
if previous == None:
self.head = None
#处理普遍情况
else:
previous.setNext(None)
return current.getData()
#pop(pos) 删除并返回位置 pos 处的项。它需要 pos 作为参数并返回项。假定该项在列表中。
def pop_pos(self, pos):
'''
if pos > self.size() or pos < 0:
return "Out of index!"
'''
current = self.head
count = -1
previous = None
#遍历节点,直到将current游标移动到pos位置为止
while current.getNext() != None and count != pos:
count = count + 1
previous = current
current = current.getNext()
#处理头结点为尾节点的情况
if previous == None:
self.head = None
#处理普遍情况
else:
previous.setNext(current.getNext())
return current.getData()
mylist = UnorderedList()
mylist.add(31)
mylist.add(77)
mylist.add(17)
mylist.add(93)
mylist.add(26)
mylist.add(54)
print(mylist.size())
print(mylist.search(93))
print(mylist.search(100))
mylist.add(100)
print(mylist.search(100))
print(mylist.size())
print("---------------------")
print("检验自己写的index()函数")
print(mylist.index(93))
print("---------------------")
print("检验自己写的append()函数")
mylist.append(106)
print(mylist.size())
print(mylist.index(106))
print("---------------------")
print("检验自己写的insert()函数")
mylist.insert(5,666)
print(mylist.size())
print(mylist.index(666))
print("---------------------")
print("检验insert的特殊情况")
mylist.insert(0,999)
print(mylist.size())
print(mylist.index(999))
print("---------------------")
print("检验自己写的pop_last()函数")
print(mylist.pop_last())
print(mylist.size())
print("---------------------")
print("检验自己写的pop_pos()函数")
print("应该返回93")
print(mylist.pop_pos(3))
print(mylist.size())
print("---------------------")
print(mylist.pop_last())
print(mylist.pop_last())
print(mylist.pop_last())
print(mylist.pop_last())
print(mylist.pop_last())
print(mylist.pop_last())
print(mylist.pop_last())
print(mylist.pop_last())
3.22.有序列表抽象数据结构
我们现在将考虑一种称为有序列表的列表类型。例如,如果上面所示的整数列表是有序列表(升序),则它可以写为 17,26,31,54,77和93。由于 17 是最小项,它占据第一位置。同样,由于 93 是最大的,它占据最后的位置。
有序列表的结构是项的集合,其中每个项保存基于项的一些潜在特性的相对位置。排序通常是升序或降序,并且我们假设列表项具有已经定义的有意义的比较运算。许多有序列表操作与无序列表的操作相同。
- OrderedList() 创建一个新的空列表。它不需要参数,并返回一个空列表。
- add(item) 向列表中添加一个新项。它需要 item 作为参数,并不返回任何内容。假定该 item 不在列表中。
- remove(item) 从列表中删除该项。它需要 item 作为参数并修改列表。假设项存在于列表中。
- search(item) 搜索列表中的项目。它需要 item 作为参数,并返回一个布尔值。
- isEmpty() 检查列表是否为空。它不需要参数,并返回布尔值。
- size()返回列表中的项数。它不需要参数,并返回一个整数。
- index(item) 返回项在列表中的位置。它需要 item 作为参数并返回索引。假定该项在列表中。
- pop() 删除并返回列表中的最后一个项。假设该列表至少有一个项。
- pop(pos) 删除并返回位置 pos 处的项。它需要 pos 作为参数并返回项。假定该项在列表中。
3.23.实现有序列表
为了实现有序列表,我们必须记住项的相对位置是基于一些潜在的特性。上面给出的整数的有序列表17,26,31,54,77 和 93 可以由 Figure 15 所示的链接结构表示。节点和链接结构表示项的相对位置。
为了实现 OrderedList 类,我们将使用与前面看到的无序列表相同的技术。再次,head 的引用为 None 表示为空链表(参见 Listing 8)。
当我们考虑有序列表的操作时,我们应该注意,isEmpty 和size 方法可以与无序列表一样实现,因为它们只处理链表中的节点数量,而不考虑实际项值。同样,remove 方法将正常工作,因为我们仍然需要找到该项,然后删除它。剩下的两个方法,search 和 add,将需要一些修改。
搜索无序列表需要我们一次遍历一个节点,直到找到我们正在寻找的节点或者没找到节点(None)。事实证明,相同的方法在有序列表也有效。然而,在项不在链表中的情况下,我们可以利用该顺序来尽快停止搜索。
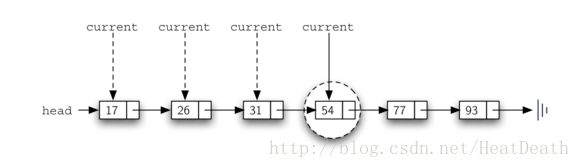
例如,Figure 16 展示了有序链表搜索值 45 。从链表的头部开始遍历,首先与 17 进行比较。由于 17 不是我们正在寻找的项,移动到下一个节点 26 。再次,这不是我们想要的,继续到 31,然后再到 54 。在这一点上,有一些不同。由于 54 不是我们正在寻找的项,我们以前的方法是继续向前迭代。然而,由于这是有序列表,一旦节点中的值变得大于我们正在搜索的项,搜索就可以停止并返回 False 。该项不可能存在于后面的链表中。
Listing 9 展示了完整的搜索方法。通过添加另一个布尔变量 stop 并将其初始化为 False(第4行),很容易合并上述新条件。 当 stop 是False(不停止)时,我们可以继续在列表中前进(第5行)。如果发现任何节点包含大于我们正在寻找的项的数据,我们将 stop 设置为 True(第9-10行)。其余行与无序列表搜索相同。
最重要的需要修改的方法是 add。 回想一下,对于无序列表,add 方法可以简单地将新节点放置在链表的头部。 这是最简单的访问点。 不幸的是,这将不再适用于有序列表。需要在现有的有序列表中查找新项所属的特定位置。
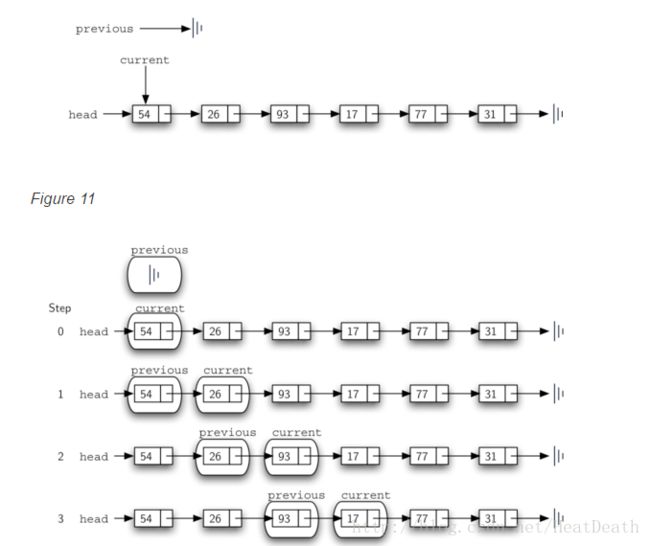
假设我们有由 17,26,54,77 和 93 组成的有序列表,并且我们要添加值31 。 add 方法必须确定新项属于 26 到 54 之间。Figure 17 展示了我们需要的设置。正如我们前面解释的,我们需要遍历链表,寻找添加新节点的地方。我们知道,当我们迭代完节点( current 变为 None)或 current 节点的值变得大于我们希望添加的项时,我们就找到了该位置。在我们的例子中,看到值 54 我们停止迭代。
class Node:
def __init__(self, initdata):
self.data = initdata
self.next = None
def getData(self):
return self.data
def getNext(self):
return self.next
def setData(self,newdata):
self.data = newdata
def setNext(self,newnext):
self.next = newnext
class OrderdList:
def __init__(self):
self.head = None
# isEmpty() 检查列表是否为空。它不需要参数,并返回布尔值。
def isEmpty(self):
return self.head == None
# add(item) 向列表中添加一个新项。它需要 item 作为参数,并不返回任何内容。假定该 item 不在列表中。
def add(self, item):
# 链表的每项必须驻留在节点对象中
temp = Node(item)
# 更改新节点的下一个引用以引用旧链表的第一个节点
temp.setNext(self.head)
# 修改链表的头以引用新节点
self.head = temp
# size()返回列表中的项数。它不需要参数,并返回一个整数。
def size(self):
current = self.head
count = 0
while current != None:
count = count + 1
current = current.getNext()
return count
def search(self, item):
current = self.head
found = False
stop = False
while current != None and not stop:
if current.getData() == item:
found = True
else:
if current.getData() > item:
stop = True
else:
current = current.getNext()
return found
def add(self, item):
current = self.head
previous = None
stop = False
while current != None and not stop:
if current.getData() > item:
stop = True
else:
previous = current
current =current.getNext()
temp = Node(item)
if previous == None:
temp.setNext(self.head)
self.head = temp
else:
temp.setNext(current)
previous.setNext(temp)
3.23.1.链表分析
为了分析链表操作的复杂性,我们需要考虑它们是否需要遍历。考虑具有 n 个节点的链表。 isEmpty 方法是 O(1),因为它需要一个步骤来检查头的引用为 None。另一方面,size 将总是需要 n 个步骤,因为不从头到尾地移动没法知道有多少节点在链表中。因此,长度为 O(n)。将项添加到无序列表始终是O(1),因为我们只是将新节点放置在链表的头部。但是,搜索和删除,以及添加有序列表,都需要遍历过程。虽然平均他们可能只需要遍历节点的一半,这些方法都是 O(n),因为在最坏的情况下,都将处理列表中的每个节点。
3.24.总结
线性数据结构以有序的方式保存它们的数据。
- 栈是维持 LIFO,后进先出,排序的简单数据结构。
- 栈的基本操作是 push,pop和 isEmpty。
- 队列是维护 FIFO(先进先出)排序的简单数据结构。
- 队列的基本操作是 enqueue,dequeue 和 isEmpty。
- 前缀,中缀和后缀都是写表达式的方法。
- 栈对于设计计算解析表达式算法非常有用。
- 栈可以提供反转特性。
- 队列可以帮助构建定时仿真。
- 模拟使用随机数生成器来创建真实情况,并帮助我们回答“假设”类型的问题。
- Deques 是允许类似栈和队列的混合行为的数据结构。
- deque 的基本操作是 addFront,addRear,removeFront,removeRear 和 isEmpty。
- 列表是项的集合,其中每个项目保存相对位置。
- 链表实现保持逻辑顺序,而不需要物理存储要求。
- 修改链表头是一种特殊情况。
3.26. Discussion Questions
- Convert the following values to binary using “divide by 2.” Show the stack of remainders.
- 17
- 45
- 96
- Convert the following infix expressions to prefix (use full parentheses):
- (A+B)(C+D)(E+F)
- A+((B+C)*(D+E))
- A*B*C*D+E+F
- Convert the above infix expressions to postfix (use full parentheses).
- Convert the above infix expressions to postfix using the direct conversion algorithm. Show the stack as the conversion takes place.
- Evaluate the following postfix expressions. Show the stack as each operand and operator is processed.
- 2 3 * 4 +
- 1 2 + 3 + 4 + 5 +
- 1 2 3 4 5 * + * +
- The alternative implementation of the Queue ADT is to use a list such that the rear of the queue is at the end of the list. What would this mean for Big-O performance?
- What is the result of carrying out both steps of the linked list add method in reverse order? What kind of reference results? What types of problems may result?
- Explain how the linked list remove method works when the item to be removed is in the last node.
- Explain how the remove method works when the item is in the only node in the linked list.
3.27编程练习
1.修改中缀表达式转为后缀表达式的算法使之能处理错误输入。
2.修改后缀表达式求值的算法使之能处理错误输入。
3.实现一个结合了中缀到后缀的转化法和后缀的求值算法的直接求中缀表达式值的方法。你的求值法应该从左至右处理中缀表达式中的符号,并且使用两个栈来完成求值,一个存储操作数,一个存储操作符。
4.将上一题的中缀求值法转化为一个计算器。
5.实现一个Queue,使用一个list使Queue的尾部在list的末端。
6.设计并实现一个实验,对以上两种Queue进行基准比较。你从这个实验中学到了什么?
7.实现一个队列并使它的enqueue和dequeue方法平均时间复杂度都是O(1)。也就是说,在大多数情况下enqueue和dequeue都是O(1),除了在一种特殊情况下dequeue可能为O(n)。
8. 考虑一个现实生活中的情况。制定一个问题,然后设计一个可以帮助解决问题的模拟实验。可能的情况包括:
a)洗车店一字排开的汽车
b)在杂货店结账的顾客
C)在跑道起飞、降落的飞机
d)一个银行柜员
一定要解释清楚做的任何假设,并且提供该方案必须包含的和概率有关的数据。
9.修改热土豆模拟实验,采用一个随机选择的数值,使每轮实验不能通过前一
次实验来预测。
10.实现基数排序。十进制的基数排序是一个使用了“箱的集合”(包括一个主箱和10 个数字箱)的机械分选技术。每个箱像队列(Queue)一样,根据数据项的到达顺序排好并保持它们的值。算法开始时,将每一个待排序数值放入主箱中。然后对每一个数值进行逐位的分析。每个从主箱最前端取出的数值,将根据其相应位上的数字放在对应的数字箱中。比如,考虑个位数字,534被放置在数字箱4,667被放置在数字箱7。一旦所有的数值都被放置在相应的数字箱中,所有数值都按照从箱0到箱9的顺序,依次被取出,重新排入主箱中。该过程继续考虑十位数字,百位数字,等等。当最后一位被处理完后,主箱中就包含了排好序的数值。
11.括号匹配问题的另一个例子是超文本标记语言(HTML)。在HTML 中,标记以开始(opening tag,)的形式存在,它们必须成对出现来正确地描述web文档。这个非常简单的HTML文档:
只是为了表明语言中标记的匹配和嵌套结构。写一个程序,它可以检查HTML文档中是否有匹配的开始和结束标记。
<html>
<head>
<title>
Example
title>
head>
<body>
<h1>Hello, worldh1>
body>
html>12.扩展Listing 2.15的程序来处理带空格的回文序列。比如,I PREFER PI是一个回文序列,因为如果忽略空格,它向前和向后读是一样的。
13.为了实现length方法,我们在链表中计算节点的数目。一种代替的方法是链表中的节点的数目作为附加的数据片段储存在链表表头中。修改无序列表类,包含这个信息并且重新编写length方法。
14.实现remove方法,使得当列表中没有相应数据项的时候它能正常运行。
15.修改列表使它允许重复。有哪些方法将受到这种变化的影响?
16.实现无序列表类的__str__方法。对于列表而言,什么是一个好的字符串形式的表现?
17.实现__str__方法,使列表以Python的形式表现出来(用方括号)。
18.实现无序列表中的其他操作(append, index, pop, insert)。
19.实现一个无序列表的切片方法。它包含start和stop两个参数,返回一个从start位置开始向后到stop位置但不包含stop位置的列表的副本。
20.实现定义在OrderedList里的其他功能。
21.考虑无序和有序列表之间的关系。有没有可能将有序列表作为无序列表的一个继承,从而更有效的实现有序表?实现这个继承体系。
22.实现一个使用链表的栈。
23.实现一个使用链表的队列。
24.实现一个使用链表的双端队列。
25.设计并实现一个实验,使它可以比较Python内置的list和用链表实现的list的性能。
26.设计并实现一个实验,使它可以比较用Python内置的list实现的栈、队列和用链表实现的栈、队列的性能。
27.上述链表的实现被称为单向链表(singly linked list),因为每个节点在序列中有单一的对下一个节点的引用。另一种代替的实现方式被称为双向链表(doubly linked list)。在此实现中,每个节点都有对下一个节点的引用(通常称为“后继”next)和对前一个节点的引用(通常称为“前驱”back)。链表表头同样有两个引用,一个指向链表的第一个节点,一个指向最后一个。用Python实现这段代码。
28.实现一个可以有平均值的队列。