点云处理学习笔记（九）-- 模板匹配理论学习

1  模型描述和投票方案

1.1  模型描述

    首先，我们假设待匹配的场景（Scene）与用于匹配的模型（Model）都是由有限个有向点构成的，也就是说这里面的每个点都有一个对应的法向量（这样的表现特征可以很容易从网格（Mesh）或者点云（Clouds）中计算出来）。

    待匹配的场景可以用所有场景中的所有场景点进行描述：

    用于匹配的模型则可以用模型中的所有模型点进行描述：

   全局模型描述在离线阶段进行完成创建。

1.2  投票方案

    完成全局模型描述后，在在线阶段，从场景点中选择一系列的场景点作为参考点集。而场景点中的其余点则与参考点集构成相应的点对特征。这些场景点的点对特征会与全局模型描述中的特征进行匹配，并恢复一系列潜在的特征。每一个潜在的场景特征点对与模型的特征匹配，都会通过投票方案给对应的位姿进行投票，而这个位姿会相对于参考点进行参数化。投票方案最终会返回一个最优的位姿。

2  具体实现

2.1  点对特征

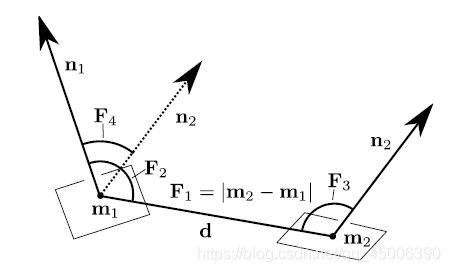
    利用点对特征来描述两个有向点之间的相对位置和朝向，如下图所示：

图2.1  点对特征

    在上图中，m1与m2是模型中的一组点对。n1是m1的法向量，n2是m2的法向量，F1是两点之间的相对距离，F2和F3分别是两点法向量与两点之间的距离F1所形成的角度，F4是F2与F3的角度之差。

    综上所述，对于点对m1和m2，我们可以设 d = m2 - m1，并由此给出点对特征F：

    利用点对特征可以进行后续的全局模型描述以及寻找场景中感兴趣的物体。

2.2  全局模型描述

    利用2.1节中的点对特征可以在离线阶段完成全局模型描述。模型的描述是由一系列具有相同特征向量的点对特征所构成的，为了能够将这些点对特征集合起来，我们需要计算所有模型表面的点对特征：

    采样的步长和采样的角度由和分别表述。所有具有相等离散形式的特征向量被集合起来。

    全局模型描述是场景中被采样的点对特征到模型的映射。形式上，我们可以将这样的映射写作：

    四维的点对特征（在2.1节中定义的F）映射到模型中的所有具有相等特征向量的点对集合A，这一过程可以可以用下图来表述：

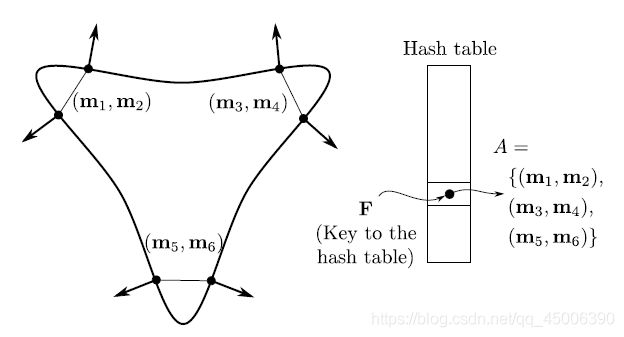
图2.2  模型描述示意图

    图2.2左侧是一个物体上具有相同特征向量的三组模型点对，这三组模型点对会被收集至同一个集合A。实际上，这一模型描述的过程是由哈希表完成的，该哈希表的索引是场景中被采样的特征F。对于所有模型点对的特征Fm而言，如果Fm与场景点对的特征Fs相似，那么Fm就可以被作为键值的Fs，在一定的时间内，从哈希表中搜索到。

2.3  投票方案

2.3.1  局部坐标

    假设，在场景点中随机选取一个参考点，假设这个参考点正好落在我们尝试进行模板匹配的物体表面。如果这个假设是正确的，那么在模型的表面一定会存在一个参考点，这个参考点与选取的场景参考点一致。将这两个点以及他们的法向量进行对齐后，模型就可以以场景参考点的法向量为旋转轴线，旋转一定的角度使模型与场景对齐。

    这样做去除了场景中模型的一个自由度。由模型到场景的刚性运动可以用模型上的一个参考点和一个旋转角度来描述。我们称为场景参考点的模型局部坐标。

    在2.2节模型描述中，通过相似的特征向量F，我们将模型点对与场景点对进行了对齐。因此，由模型局部坐标到场景坐标下的变换，可以定义为：

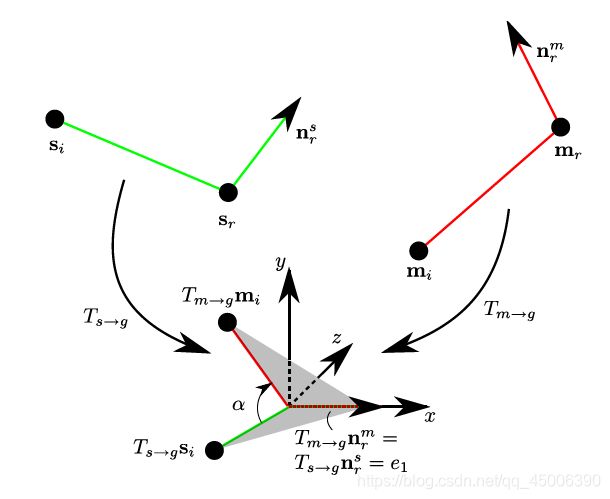
    推导过程如下图：

图2.3  模型坐标与场景坐标至之间的转换

    由于场景点对与模型点对具有相同的特征F，因此他们具有相同的点对间距和同向的点对朝向。转换将模型参考点移至原点，并旋转其法向量使其与X轴重合，转换对场景参考点对进行相同的操作。由于与可能无法对齐，因此可以通过旋转一个角度使得场景点对与模型点对能够对齐。

    经过转换的局部坐标只拥有三个自由度（一个是旋转角度，另外两个则用于描述模型表面上的点），而一个传统的三维刚体运动则需要六个自由度来进行描述。

2.3.2  投票方案

    对于一个固定的场景参考点，我们希望可以找到一个最优的局部坐标，能够使得场景中落在模型上的点的个数最大化。为了达到这一目的，可以采用与广义霍夫变换相似的投票方案，并且由于局部坐标只有三个自由度，这一投票方案也更加有效。一旦找到了最优的局部坐标，目标物体的全局位姿就可以被恢复。

    为了完成这一投票方案，需要建立一个二维的累加器数组。这个数组的行数，记作，与模型的采样点数相同；数组的列数，记作，与旋转角度的采样步长一致。该累加器数组代表了，对于一个固定的参考点，局部坐标的离散空间。

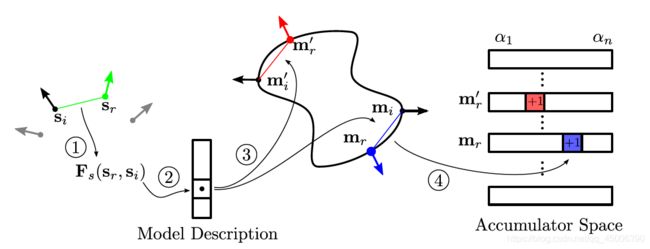
图2.4  投票方案

    在实际的投票过程中，需要在模型表面搜索与场景参考点对具有相同的点距与法向量（即特征Fs）的模型参考点对。这一搜索过程，解决了在模型上这些待匹配的场景点对可能在哪里的问题，并且执行这一搜索操作也利用到了之前所计算的场景点对特征Fs，并将其作为哈希表的索引键值，以便在模型上寻找与之相对应的所有具有相同特征的模型点对。

    对于每个搜索到的模型参考点对，也就是场景点对在模型上的所有可能位置而言，模型点对到场景点对的旋转角度，可以通过局部坐标中推导的表达式进行计算。每完成一次搜索，就使相应的局部坐标的投票数加一。

    当所有的场景点完成搜索后，累加器中的得分最高的数组与最优局部坐标一致，通过这一数组就可以计算出刚体变换。为了能够获得更加稳健的效果，累加器中所有获得一定投票数的数组都将被用来计刚体变换。

2.3.3  有效的投票循环

    为了可以获得更高效的物体检测算法，下面会展示上述的投票方案如何有效执行。

    为了能够加速2.3.1节中的每个点对的局部坐标的求解过程，我们将旋转角度分解为以下两部分：

    分解后的和分别由模型点对和场景点对确定。

    根据对旋转角度的分解以及局部坐标的求解，我们可以推导以下方程：

    也就是说 t 位于由x轴和y轴非负半轴所确定的半平面内。对于模型或者场景中的每个点对而言，他们的 t 都是独一无二的。

    每个模型点对的在离线阶段就进行了预先计算并存储在模型描述中，而每个场景点对的只需要被计算一次，而最终的旋转角度只需要对两个角度简单做差即可。

2.3.4  位姿聚类

    如果场景参考点位于物体表面，上述的投票方案就会识别出物体的位姿。因此，需要选取多个不同的参考点，来确保他们中的一个点可以落在待搜索的物体表面。正如前文所述，每一个参考点都会根据其在累加器数组中的峰值返回一系列可能的位姿。这些返回的位姿，由于场景与模型之间不同的采样率以及局部坐标的旋转采样，只能对物体的表面进行粗略的估计。下面我们将介绍一个额外的步骤，不仅能滤除不正确的位姿，而且能提高最终结果的精确度。

    为了达到这一目的，所有恢复的位姿都被放入一个聚类器中进行聚类，在不超过阈值的情况下，该聚类器中的所有位姿在平移和旋转上都没有区别。聚类器的得分就是其中包含的所有位姿的得分总和，而每一个位姿的得分则是他们在投票算法中获得的分数。在找到得分最高的聚类器之后，最终的位姿就可以通过计算该聚类器中的位姿得分的平均值来获得。

    由于场景中的物体可能在不同的距离上，因此这个方法可能会返回多个聚类器。通过分离低分位姿，位姿聚类器提高了算法的稳定性，同时，以聚类器中位姿的平均值来求取最终位姿结果，提高了最终位姿的精度。

3  参数设置

    特征空间的采样步长与模型的直径相关，关系表达式可以写作：

    默认情况下，采样率被设置为0.05。这使得采样步长与模型的直径可以区分开来。

    法线的朝向被划分为个区间，默认情况下：

    这样设置允许法线方向相对于正确的法线方向有最高12°（360°/30）的偏移量。

    模型和场景点云都进行了下采样，因此，下采样后的点对之间的最小距离只有正常采样步长的1/5，下采样后的点集用作参考点。

    在对点云进行重新采样后，每个点的法向量都通过将平面拟合至每个点的邻域来重新计算。这样做既可以法向量与采样时一致，又可以避免因细节造成的问题，如表面的褶皱。