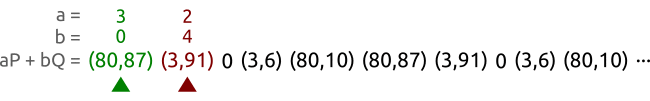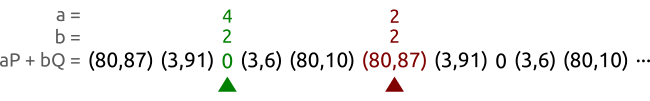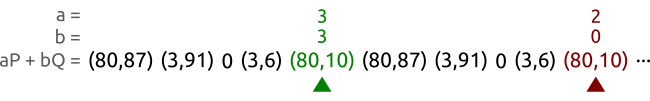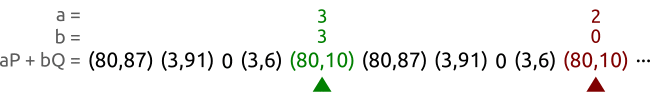椭圆曲线介绍(四):椭圆曲线安全性,与RSA对比
内容来自ANDREA CORBELLINI的椭圆曲线密码学的介绍:Elliptic Curve Cryptography: a gentle introduction
本文是椭圆曲线介绍中的第四篇:椭圆曲线的安全性部分。
在上一篇博客中,我们已经介绍了两种椭圆曲线上面的密码学算法:ECDH和ECDSA。注意到两种算法的安全性都是基于了椭圆曲线中的离散对数问题。但是,还没有严谨的数学证明说明离散对数问题确实是困难的,只是学界形成了这样一种共识,那有什么证据可以让我们相信这个共识?
那么在这个博客的第一部分,我们就要来理清椭圆曲线中的离散对数问题究竟有多难解决。
在第二部分,我们来回答以下的问题:为什么RSA类型(算术模类型)的密码系统已经有那么多好用的算法了,还需要提出基于椭圆曲线的密码学算法。
文章目录
- 解决离散对数问题
-
- 小步大步法(Baby-step, giant-step)
- Pollard's ρ \rho ρ方法
-
- 龟兔赛跑
- 各种攻击算法的效率对比
- 最后的总结
- Shor的算法
- ECC和RSA对比
- NSA背后的危险
解决离散对数问题
我们接下来要介绍两种高效地计算椭圆曲线离散对数的方法:1.baby-step,giant-step方法,小步大步法。2.Pollard’s rho方法。
在开始介绍这两个方法之前,回忆一下离散对数问题是什么:给定两个点 P P P和 Q Q Q,计算出一个数字 x x x使得 Q = x P Q=xP Q=xP。 P P P和 Q Q Q两点属于椭圆曲线上的同一个子群,该子群的生成元为 G G G,阶为 n n n。
小步大步法(Baby-step, giant-step)
在开始介绍算法之前,先想一想,我们可以将任意的整数写作 x = a m + b x=am+b x=am+b。比如 10 = 2 ⋅ 3 + 4 10=2\cdot 3+4 10=2⋅3+4。
因此,也可以把离散对数难题的形式转换为:
Q = x P Q = ( a m + b ) P Q = a m P + b P Q − a m P = b P \begin{aligned} Q&=xP\\ Q&=(am+b)P\\ Q&=amP+bP\\ Q-amP&=bP \end{aligned} QQQQ−amP=xP=(am+b)P=amP+bP=bP
小步大步法更像是一个折中的方案,与暴力搜索相比,我们只需要计算几个 b P bP bP的值,以及几个 Q − a m P Q-amP Q−amP的值。算法的步骤如下:
- 计算 m = ⌈ n ⌉ m=\lceil \sqrt{n} \rceil m=⌈n⌉
- 对于 b ∈ { 0 , . . . , m } b \in \{0,...,m\} b∈{0,...,m},计算 b P bP bP并存于哈希表中。
- 对于 a ∈ { 0 , . . . , m } a \in \{0,...,m\} a∈{0,...,m}:
- 计算 a m P amP amP;
- 计算 Q − a m P Q-amP Q−amP;
- 查看哈希表中是否存在 Q − a m P = b P Q-amP=bP Q−amP=bP;
- 如果存在的话,那就返回 x = a m + b x=am+b x=am+b。
可以观察到,一开始计算的点 b P bP bP之间的差距为 1 1 1,记作小步,然后在第二部分中,两个点之间的差距为 m m m,其中 m m m是一个很大的数字,所以记作大步。
下面解释一下这个算法为什么是对的,仅用小步大步怎么保证所有元素都被遍历了。我们知道 Q = a m P + b P Q=amP+bP Q=amP+bP,那考虑:
- 当 a = 0 a=0 a=0的时候,我们就在验证是否 Q = b P Q=bP Q=bP,因为 b b b是在 0 0 0到 m m m中的一个数,所以我们就是在确认 Q Q Q是否为 0 P 0P 0P到 m P mP mP。
- 当 a = 1 a=1 a=1的时候,我们在验证是否 Q = m P + b P Q=mP+bP Q=mP+bP,我们是在确认 Q Q Q是否为 m P mP mP到 2 m P 2mP 2mP。
- 当 a = 2 a=2 a=2的时候,我们是在确认 Q Q Q是否为 2 m P 2mP 2mP到 3 m P 3mP 3mP。
- …
- 当 a = m − 1 a=m-1 a=m−1的时候,我们是在确认 Q Q Q是否为 ( m − 1 ) m P (m-1)mP (m−1)mP到 m 2 P = n P m^2P=nP m2P=nP。
因此,我们其实是确认了 Q Q Q是否为 0 P 0P 0P到 n P nP nP中的某个点,而且我们只执行了 2 m 2m 2m次加法或乘法操作。
如果将查询哈希表的复杂度记为 O ( 1 ) O(1) O(1),那么这个算法的时间复杂度为 O ( n ) O(\sqrt{n}) O(n),空间复杂度为 O ( 2 k ) O(2^{k}) O(2k), k k k为点的比特长度。虽然仍然是幂次时间的,但是比暴力搜索已经好多了。
Pollard’s ρ \rho ρ方法
Pollard的rho方法和小步大步法一样是一个 O ( n ) O(\sqrt{n}) O(n)复杂度的算法,但是其空间复杂度只是 O ( 1 ) O(1) O(1)。
再次回忆一下离散对数问题是什么:给定两个点 P P P和 Q Q Q,计算出一个数字 x x x使得 Q = x P Q=xP Q=xP。在Pollard’s ρ \rho ρ方法中,我们解决的问题稍微有些不同:给定两个点 P P P和 Q Q Q,找到四个数 a , b , A , B a,b,A,B a,b,A,B满足 a P + b Q = A P + B Q aP+bQ=AP+BQ aP+bQ=AP+BQ。
如果可以找到这样一个式子,那就可以用这个式子来解决离散对数问题:
a P + b Q = A P + B Q a P + b x P = A P + B x P ( a + b x ) P = ( A + B x ) P ( a − A ) P = ( B − b ) x P \begin{aligned} a P+b Q &=A P+B Q \\ a P+b x P &=A P+B x P \\ (a+b x) P &=(A+B x) P \\ (a-A) P &=(B-b) x P \end{aligned} aP+bQaP+bxP(a+bx)P(a−A)P=AP+BQ=AP+BxP=(A+Bx)P=(B−b)xP
现在可以通过两边除 P P P的方式来消除 P P P,不要忘记所有的系数都是在 m o d n \bmod n modn范围内的,因此:
a − A ≡ ( B − b ) x m o d n x = ( a − A ) ( B − b ) − 1 m o d n \begin{aligned} a-A & \equiv(B-b) x \quad\bmod n \\ x &=(a-A)(B-b)^{-1} \bmod n \end{aligned} a−Ax≡(B−b)xmodn=(a−A)(B−b)−1modn
Pollard rho方法的宗旨非常简单,我们随机生成一些点 X 1 , X 2 , . . . X_1,X_2,... X1,X2,...,其中 X i = a i P + b i Q X_i = a_iP + b_iQ Xi=aiP+biQ。可以用伪随机函数来生成:
( a i + 1 , b i + 1 ) = f ( X i ) (a_{i+1},b_{i+1})=f(X_i) (ai+1,bi+1)=f(Xi)
这个函数的意思是,将 X i X_i Xi作为输入,得到 X i + 1 X_{i+1} Xi+1的系数 a i + 1 , b i + 1 a_{i+1},b_{i+1} ai+1,bi+1,然后可以再将 X i + 1 X_{i+1} Xi+1作为输入,继续运算,这个过程可以一直运算下去。
f f f的内部逻辑其实无关紧要,重要的是 f f f是由当前的点得出下一个点,而所有 f f f得到的 a i , b i a_i,b_i ai,bi我们都是知道的。
只要一直运算下去,我们总归会得到一个循环的,也就是找到了 X j = X i X_j=X_i Xj=Xi。

至于为什么一定会出现这样的循环,理由很简单:椭圆曲线群中的点的数量是有限的,因此总归会出现一个循环。一旦我们遇到了一次循环,那就可以来解决上面的离散对数问题。
现在的新问题来了:怎么更快的找到这样一个循环?
龟兔赛跑
一个比较快的找循环的方法是龟兔赛跑法。下图展示了龟兔赛跑法的原理,其实也是Pollard’s rho方法。
比如曲线是 y 2 ≡ x 3 + 2 x + 3 ( m o d 97 ) y^2 \equiv x^3 +2x +3 \pmod{97} y2≡x3+2x+3(mod97),上面的点为 P = ( 3 , 6 ) P=(3,6) P=(3,6),以及 Q = ( 80 , 87 ) Q=(80,87) Q=(80,87)。这些点属于一个阶为5的子群。我们用两个不同的参数 ( a , b ) ( A , B ) (a,b)(A,B) (a,b)(A,B)来遍历这些 a P + b Q aP+bQ aP+bQ的对,直到它们所指向的点相等。在上面的例子中,我们找到了 ( 3 , 3 ) (3,3) (3,3)和 ( 2 , 0 ) (2,0) (2,0)是一样的,于是就可以计算出 x = ( 3 − 2 ) ( 0 − 3 ) − 1 m o d 5 = 3 x=(3-2)(0-3)^{-1}\bmod 5 =3 x=(3−2)(0−3)−1mod5=3。那就得出了离散对数难题的解: Q = 3 P Q=3P Q=3P。
我们选择两个动物:乌龟和兔子,让他们从左到右跑。乌龟(绿点)比红点(兔子)的速度要慢一点。乌龟一次走一格,兔子一次走两格。
过了一段时间之后,龟和兔找到了一个相同的点,但是他们的参数点不同。或者用参数来表示的话,就是乌龟找到了一对参数 ( a , b ) (a,b) (a,b),兔子找打了一对参数 ( A , B ) (A,B) (A,B),使得 a P + b Q = A P + B Q aP+bQ=AP+BQ aP+bQ=AP+BQ。
很容易看出来这样的方案只需要常数的内存( O ( 1 ) O(1) O(1)的空间复杂度)。时间复杂度不太好计算,但是可以通过一个概率证明时间复杂度是 O ( n ) O(\sqrt{n}) O(n)级别的。这个证明是基于生日悖论的:生日悖论考虑的是两个人生日相同的概率,而我们考虑的是两对 ( a , b ) (a,b) (a,b)能得到相同点的概率。
各种攻击算法的效率对比
将穷举算法,pollard’s rho算法,大步小步法放在一起进行比较,代码放在这里"几种椭圆曲线攻击算法对比python代码"。
运行结果如下:
Curve order: 10331
Using bruteforce
Computing all logarithms: 100.00% done
Took 2m 31s (5193 steps on average)
Using babygiantstep
Computing all logarithms: 100.00% done
Took 0m 6s (152 steps on average)
Using pollardsrho
Computing all logarithms: 100.00% done
Took 0m 21s (138 steps on average)
不难猜测到穷举是最慢的。小步大步法最快,Pollard’s rho方法差不多比小步大步法要慢三倍左右。(尽管他的步数和使用的内存最少)。
另外可以从平均步数上看一下这三个算法,穷举平均用了5193步,基本上是椭圆曲线阶的一般。小步大步法和Pollard’s rho方法都是接近10331的平方根的步数。
最后的总结
虽然我们讨论了几个方法,他们并不能很有效地破解椭圆曲线的离散对数问题。但不代表这些算法完全不可行,也许可以继续做优化,比如硬件上面的突破。
虽然目前没有离散对数问题的有效解决方法,但不代表未来不会有。
Shor的算法
虽然如今的方法是不可行的,但是未来的量子计算机中,存在一种量子算法可以破解离散对数问题,他就是Shor算法。它的时间复杂度为 O ( log n ) 3 O(\log n)^3 O(logn)3,空间复杂度为 O ( log n ) O(\log n) O(logn)。
尽管现在的量子计算还不足以运行Shor算法,但是向着后量子密码迁移已经是一个必要的事情了。我们今天用的加密算法是安全的,不代表明天他还安全。
ECC和RSA对比
现在先把量子计算机放在一边,那是之后的问题。现在的问题是,已经在有RSA的情况下,为什么还需要ECC的算法?
NIST给出了一个直接的回答,他们给出了相同安全等级下两个算法的密钥大小:
| RSA key size (bits) | ECC key size (bits) |
|---|---|
| 1024 | 160 |
| 2048 | 224 |
| 3072 | 256 |
| 7680 | 384 |
| 15360 | 521 |
注意到RSA的密钥长度与ECC的密钥长度之间不存在线性关系。也就是说,RSA的密钥增加到两倍的情况下,ECC并没有增倍。而且ECC不仅存储密钥的开销会比较小,而且密钥生成和签名运算都会比RSA要快很多。
但为什么会这样呢?因为解决ECC上面的离散对数问题比解决有限域中的离散对数要困难一些。整数上面的离散对数问题一般是通过普通数域筛选法,可以较快的分解整数,从而解决离散对数问题。
NSA背后的危险
我们目前为止讨论的都是算法和算数的问题。但有一个更重要也更复杂的因素,就是人。
在上一个博客中我们提到了有些椭圆曲线是不安全的,为了防止不明来源的曲线,我们采用了随机数种子来生成全局参数的方法。如果我们看一下NIST公布的椭圆曲线,我们可以验证他们确实是由随机数生成的。
如果我们搜一下Nothing up my sleeve number,可以看到:
- MD5的随机数是由整数运算sin函数得到的
- Blowfish的随机数是 π \pi π的前几位
- RC5的随机数是来自自然对数 e e e和黄金分割
这些数字我们可以相信他们是随机的。因为我们自己可以验证出这些数。
而NIST公布的随机数种子是怎么得来的?,我们不知道。所以这些随机数种子其实并没有公信力。
NIST有没有可能通过穷举随机数种子的方式来找到了一个不安全的椭圆曲线并将他们公布? 也不是没可能。目前来说NIST已经有公布不安全的随机数生成器的前科了。所以他们也有公布一个不安全的椭圆曲线的犯罪可能(doge)。
考虑到椭圆曲线的参数问题,其实这方面是RSA胜出的,因为RSA不需要指定某个素数,只需要足够长都能用。而椭圆曲线要精心选取来避开一些不安全的参数。
但NIST公布的椭圆曲线现在用的多吗?答案是是的,在TLS层就用了NIST的曲线,如果搜一下会发现现在的ECDHE和ECDSA,他们的证书是基于prime256v1(也就是secp256p1)。