Multilevel domain decomposition-based architectures for physics-informed neural networks

Multilevel domain decomposition-based architectures for physics-informed neural networks

FBPINN

Finite Basis Physics-Informed Neural Networks (FBPINNs)提出了有限基物理信息神经网络（FBPINN），其目的是通过使用重叠域分解（DD）方法来提高 PINN 的性能。FBPINN 中不使用单个神经网络来近似微分方程的解，而是将许多较小的神经网络放置在重叠的子域中并加在一起以表示解。一方面，FBPINN 可以被视为 PINN 的基于域分解的网络架构。另一方面，通过采用这种“分而治之”的方法，全局 PINN 优化问题转化为许多较小的局部优化问题，这些问题由于子域及其全局定义的损失函数的重叠而隐式耦合。其结果表明，在求解具有高频和多尺度解的微分方程时，这显着提高了PINN的精度并降低了训练成本。

本文将通过将多级建模纳入其设计中来显着扩展 FBPINN。特别是，作者在解决方案中没有使用单域分解，而是添加了多个级别的重叠域分解。这个想法受到经典 DDM 的启发，在使用大量子域时，需要粗略的级别来实现数值可扩展性。此外，为了评估多级 FBPINN 的性能，作者定义了强和弱缩放测试，用于测量 PINN 和 FBPINN 的准确性如何随计算量和解决方案复杂性进行缩放，类似于经典 DDM 中常用的强和弱缩放测试。

FBPINN数学表示

首先，将全局解域 $\Omega$ 分解为 $J$ 个重叠子域 $\{{\Omega }_j{\}}_{j=1}^J$ 如下图

然后，对于每个子域 ${\Omega }_j$ ，定义一个网络函数空间
$${\mathcal{V}}_j=\{v_j(\mathbf{x},{\mathbf{\theta }}_j)\mid \mathbf{x}\in {\Omega }_j,{\mathbf{\theta }}_j\in {\Theta }_j\}$$
其中 ${\mathfrak{v}}_j(\mathbf{x},{\mathbf{\theta }}_j)$ 是放置在每个子域中的神经网络，${\Theta }_j={\mathbb{R}}^{K_j}$ 是所有可能的网络参数的线性空间。这里，$K_j$是本地网络参数的数量，由网络架构决定。

接下来，通过将每个网络与窗口函数 ${\omega }_j(x)$ 相乘，将每个子域网络限制在其子域内，其中 $\mathrm{supp}({\omega }_j)\subset {\Omega }_j$ 。
$$\sum _{j=1}^J{\omega }_j\equiv 1\mathrm{on}\Omega$$
给定网络函数和窗口函数的空间，预售可将 $\mathcal{V}$ 给出的全局空间分解定义为
$$\mathcal{V}=\sum _{j=1}^J{\omega }_j{\mathcal{V}}_j$$
这种空间分解允许将任何给定函数 $u\in \mathcal{V}$ 分解如下
$$u=\sum _{j=1}^J{\omega }_j{v}_j\mathrm{or}u(\mathbf{x},\mathbf{\theta })=\sum _{j=1}^J{\omega }_j{v}_j(\mathbf{x},{\mathbf{\theta }}_j)$$
于是，FBPINN的损失函数如下：
$$\mathcal{L}(\mathbf{\theta })=\frac{1}{N}\sum _{i=1}^N(\mathcal{N}[\mathcal{C}\sum _{j=1}^J{\omega }_j{v}_j]({\mathbf{x}}_i,{\mathbf{\theta }}_j)-f({\mathbf{x}}_i){)}^2$$
其中，$\mathcal{C}$ 为强制施加的边界条件。

Multilevel FBPINNs

多级 FBPINN 定义如下。首先，定义 $L$ 级域分解，其中每个级 $l$ 定义 $\Omega$ 与 $J(l)$ 个子域的重叠域分解，即
$$D^{(l)}={\left\{{\Omega }_j^{(l)}\right\}}_{j=1}^{J^{(l)}}$$
对于 $j=1,\dots ,J^{(l)}$ 。不失一般性，令 $J^{(1)}=1$，即在第一层只有一个子域 ${\Omega }_j^{(1)}=\Omega$。此外，可以令 $J^{(1)}<J^{(2)}<\dots <J^{(l)}$，表示子域的数量从一级增加到下一级。

接下来，可以定义每个级别的网络空间
$$V_j^{(l)}=\left\{v_j^{(l)}(\mathbf{x},{\mathbf{\theta }}_j^{(l)})\mid \mathbf{x}\in {\Omega }_j^{(l)},{\mathbf{\theta }}_j^{(l)}\in {\Theta }_j^{(l)}\right\},j=1,\dots ,J^{(l)},l=1,\dots ,L$$
与此同时，每一级的窗口函数可以定义如下：
$$\mathrm{supp}({\omega }_j^{(l)})\subset {\Omega }_j^{(l)}\mathrm{and}\sum _{j=1}^{J^{(l)}}{\omega }_j^{(l)}\equiv 1\mathrm{on}\Omega \forall l$$
于是，全局域分解可表示如下：
$$\begin{array}{r}\nu =\frac{1}{L}\sum _{l=1}^L\sum _{j=1}^{J^{(l)}}{\omega }_j^{(l)}{\nu }_j^{(l)}\end{array}$$
并使用此空间分解来分解任何给定函数 $u\in \mathcal{V}$ 如下，
$$u=\frac{1}{L}\sum _{l=1}^L\sum _{j=1}^{J^{(l)}}{\omega }_j^{(l)}{v}_j^{(l)}\mathrm{or}u(\mathbf{x},\mathbf{\theta })=\frac{1}{L}\sum _{l=1}^L\sum _{j=1}^{J^{(l)}}{\omega }_j^{(l)}{v}_j^{(l)}(\mathbf{x},{\mathbf{\theta }}_j^{(l)})$$
同样，其损失函数可以定义如下：
$$\mathcal{L}(\mathbf{\theta })=\frac{1}{N}\sum _{i=1}^N(\mathcal{N}[\mathcal{C}\frac{1}{L}\sum _{l=1}^L\sum _{j=1}^{{\mathbf{J}}^{(l)}}{\omega }_j^{(l)}{v}_j^{(l)}]({\mathbf{x}}_i,{\mathbf{\theta }}_j^{(l)})-f({\mathbf{x}}_i){)}^2$$

示例

考虑如下拉普拉斯边值问题：
$$\begin{array}{rl}-\Delta u=f& \mathrm{in}\Omega =[0,1{]}^d,\\ u=0& \mathrm{on}\partial \Omega .\end{array}$$
当 $d=1,f=8$ 时，其精确解为 $u(x)=4x(1-x)$

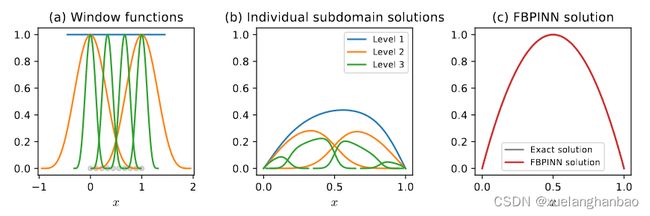
考虑3层FBPINN，其中 $J^{(1)}=1,J^{(2)}=2,J^{(3)}=4$ 其均匀域分解如下：
$${\Omega }_j^{(l)}=\{\begin{array}{ll}[0.5-\delta /2,0.5+\delta /2]& l=1,\\ \left[\frac{(j-1)-\delta /2}{J^{(l)}-1},\frac{(j-1)+\delta /2}{J^{(l)}-1}\right]& l>1,\end{array}$$
其中 $\delta$ 为重叠率。子域窗函数形成每个级别的统一分区，并由下式给出
$${\omega }_j^{(l)}=\frac{{\hat{\omega }}_j^{(l)}}{{\sum }_{j=1}^{J(l)}{\hat{\omega }}_j^{(l)}}$$
其中
$${\hat{\omega }}_j^{(l)}(x)=\{\begin{array}{ll}1& l=1\\ [1+\cos (\pi (x-{\mu }_j^{(l)})/{\sigma }_j^{(l)}){]}^2& l>1\end{array}$$
${\mu }_j^{(l)}=(j-1)/(J^{(l)}-1)$ 与 ${\sigma }_j^{(l)}=(\delta /2)/(J^{(l)}-1)$ 分别表示每个子域的中心和半宽。

结果如下：

同样考虑二维情况 $f(x_1,x_2)=32(x_1(1-x_1)+x_2(1-x_2))$ ，其精确解为 $u(x_1,x_2)=16(x_1(1-x_1)x_2(1-x_2))$

其域分解 $J^{(1)}=1\times 1=1,J^{(2)}=2\times 2=4,J^{(3)}=4\times 4=16$ 表示如下：
$${\omega }_j^{(l)}=\frac{{\hat{\omega }}_j^{(l)}}{{\sum }_{j=1}^{J(l)}{\hat{\omega }}_j^{(l)}},\mathrm{where}{\hat{\omega }}_j^{(l)}(\mathbf{x})=\{\begin{array}{ll}1& l=1\\ {\prod }_i^d[1+\cos (\pi (x_i-{\mu }_{ij}^{(l)})/{\sigma }_{ij}^{(l)}){]}^2& l>1,\end{array}$$
结果如下：

实验结果

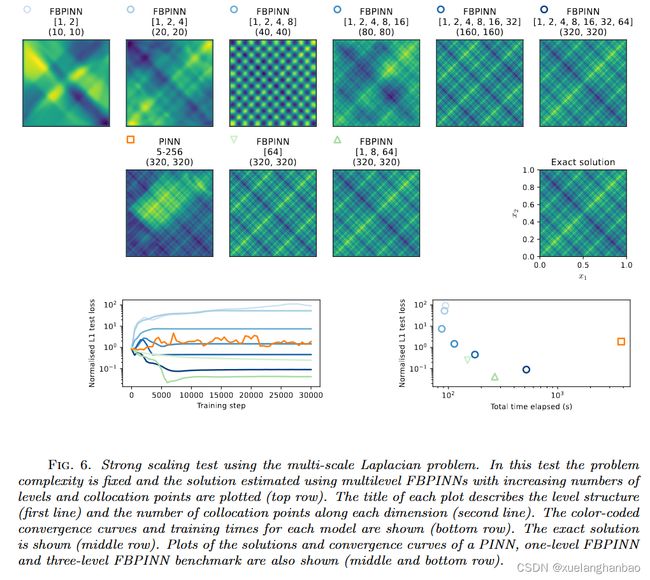
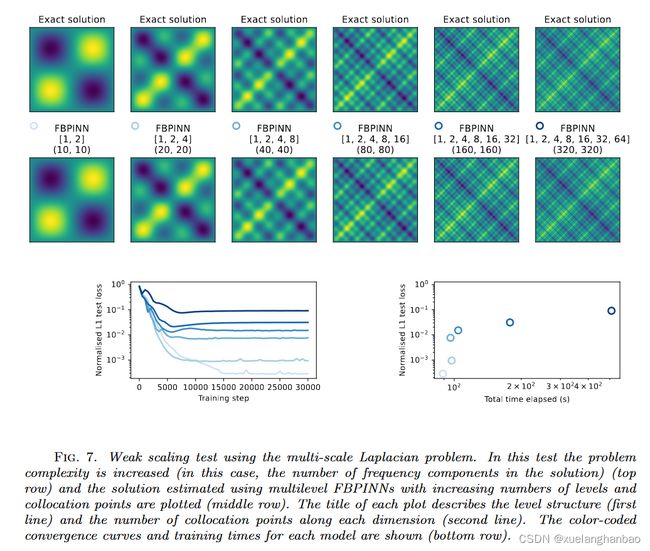
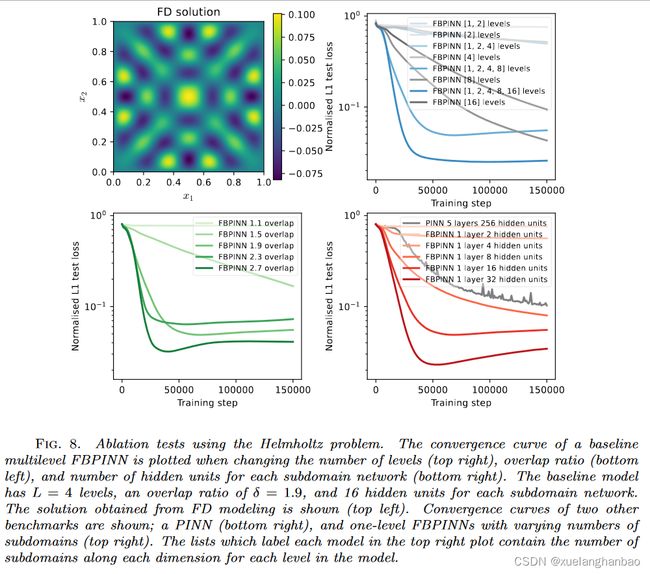
作者于多尺度拉普拉斯问题和亥姆霍兹问题都进行了强尺度和弱尺度测试。通过这些实验评估了多级 FBPINN 的准确性如何随计算量和解的复杂性进行扩展，并受到经典 DD 中常用的强和弱扩展测试的启发。它们的定义如下：

强尺度：固定问题的复杂性并增加了模型容量。

弱尺度：以相同的速度增加问题的复杂性和模型容量。

其中，增加模型容量意味着增加级别数量、子域数量、子域网络的大小和使用的配置点数量。

总结

本文相比FBPINN更进一步，模仿传统DDM方法，通过多级域分解来实现更复杂的网络结构。

感觉做法还是很好理解的，但可能是由于我对经典DDM不太熟悉，所以不太能理解作者的动机。而且这代码怎么这么抽象，看得我头疼，大概是我不熟悉jax的原因？

相关链接：

• 原文：[PDF] Multilevel domain decomposition-based architectures for physics-informed neural networks | Semantic Scholar
• 原文代码：benmoseley/FBPINNs at multilevel-paper (github.com)