《复杂约束下的多目标优化算法》阅读笔记

摘要：约束多目标优化问题(CMOP)由于需要同时考虑目标和约束，特别是当约束极其复杂时，处理起来比较困难。最近的一些算法在处理具有简单可行域的CMOP时工作得很好，然而，对于具有复杂可行域的CMOP，大多数算法的有效性显著降低。针对这一问题，本文提出了一种多阶段进化算法，在进化的不同阶段逐一添加约束，并对约束进行处理。具体地说，该算法在初始阶段只考虑了少量的约束条件，可以使种群高效地收敛到具有良好多样性的潜在可行域。随着算法进入后期阶段，在前一阶段获得的解的基础上，考虑更多的约束条件来搜索最优解。此外，还提出了一种根据对无约束Pareto前沿的影响对约束处理优先级进行排序的策略，从而加快了算法的收敛速度。在五个基准测试套件和三个实际应用上的实验结果表明，该算法在处理复杂约束的多目标进化算法时，尤其是在处理复杂约束的问题时，性能优于几种最新的约束多目标进化算法。

1 Introduction

  CMOP(Constrained multi-objective optimization problems)可以被描述为：
$$\begin{array}{rl}Minimize& \mathbf{F}(\mathbf{x})=(f_1(\mathbf{x}),...,f_m(\mathbf{x})))\\ subjectto& \mathbf{x}\in \Omega \\ & g_i(\mathbf{x})\le 0,i=1,...,p\\ & h_j(\mathbf{x})=0,j=1,...,q\end{array}$$解的约束违反程度为：
$$C(\mathbf{x})=\sum _{k=1}^p\max \left\{0,g_k\left(\mathbf{x}\right)\right\}+\sum _{\ell =1}^q\left|h_{\ell }\left(\mathbf{x}\right)\right|$$若解$\mathbf{x}$可行，则$C(\mathbf{x})=0$。
  截至目前，解决多目标优化问题的多目标进化算法（MOEAs）主要分为四类：1）基于帕累托支配的进化算法：NSGA-II[11]、SPEA2[50]；2）基于分解的进化算法：MOEA/D[46]、MOEA/D-AWA[34]；3）基于指标的进化算法：IBEA[49]、AR-MOEA[36]；4）混合型进化算法：SRA[24]、Two-Arch[40]。近年来有约束的多目标优化问题（CMOP）逐渐吸引了研究学者的注意，于是一系列求解这类问题的进化算法也被相继提出（CMOEAs），例如基于有约束的帕累托支配的NSGA-II-CDP[11]；基于两档案策略的C-TAEA[25]；以及基于两阶段搜索的ToP[27]。尽管这些方法在解决有约束多目标优化问题时表现都很不错，但是在一些特殊复杂的约束条件下，比如：离散的可行域和很大的不可行域屏障结合，或仅有狭窄的可行域等情况，并不一定能找到最优解。因此我们提出，如果能够将约束条件分阶段加入求解过程，应该可以使求解更加简单。
  遵循这一思想，本文提出了一种求解CMOP问题的多阶段进化算法。该算法将约束处理过程分成多个阶段，逐个阶段地处理约束，而不是将所有约束作为一个整体来处理。这项工作的主要贡献概括如下：
  1)提出了一种求解复杂约束条件下CMOP问题的多阶段CMOEA(MSCMO)算法。在该算法中，约束是逐个添加的，并在不同的进化阶段进行处理。在初始阶段，该算法只需处理少量的约束条件，能使种群高效地收敛到具有良好多样性的潜在可行域。对于每个阶段，考虑了更多的约束，并且可以基于在前几个阶段获得的解更容易地处理这些约束。
  2)提出了一种根据对无约束Pareto前沿的影响对约束处理优先级进行排序的策略，用于确定每个阶段需要处理的约束。在基准CMOP上的实验结果表明，提出的约束处理优先级可以加快算法的收敛速度。
  3)在基准CMOP和实际应用上的一系列实验结果表明，我们的算法与现有CMOEAS相比具有很强的竞争力，特别是在具有复杂约束的CMOP上。

2 Related works and motivation

2.1 现有的CMOEAs

  一般来说，现有的CMOEA根据它们采用的约束处理技术可以分为四类。
  第一类是惩罚函数法。其主要思想是根据个体违反约束的程度来构造惩罚项，通过在目标函数中加入惩罚项，构造了惩罚适应度函数$fitness(\mathbf{x})$。然后，用$fitness(\mathbf{x})$来评价个体。惩罚函数方法可分为：死刑函数[30]、静态惩罚函数[18]、动态惩罚函数[15]和自适应惩罚函数[26,35,19]。其中，自适应惩罚函数具有更好的性能，因为它可以利用搜索过程中的反馈信息来动态调整参数。文[26]将惩罚函数与粗糙集理论相结合，根据个体违反约束的情况自适应调整惩罚系数。文献[35]提出了一种新的基于模糊规则的罚函数方法，用于求解约束优化问题，该问题使用模糊推理系统自适应地确定罚函数的值。文[19]将偏好转化为进化多目标优化的约束条件，并采用基于罚函数法的约束支配原则处理约束条件。
  第二类是将目标和约束分开。具体地说，这一类可以分为三类：可行性规则、随机排序法和$ϵ$-约束方法。对于可行性准则，可行解优于不可行解。Deb在[7]中提出的可行性规则CDP是最流行的约束处理技术之一，在以下三个条件下，一个解$\mathbf{x}$被认为优于另一个解$\mathbf{y}$：
1.$\mathbf{x}$可行而$\mathbf{y}$不可行；
2.$\mathbf{x}$和$\mathbf{y}$都可行，但$\mathbf{x}$的目标函数值由于$\mathbf{y}$；
3.$\mathbf{x}$和$\mathbf{y}$都不可行，但是$\mathbf{x}$的约束违反程度低于$\mathbf{y}$。
在[29]中，每个解的一个新的适应度函数被定义为两种排序的加权和：一种是基于CDP的解的排序，另一种是基于Pareto支配的解的排序。在[45]中，随机排序方法中的概率参数Pf可以随着种群在差异进化(DE)框架下的演化而动态变化。$ϵ$-约束方法提供了对不可行解的松弛。对于约束违约度小于$ϵ$-的个体，其解被认为是可行的。反之，对于违反约束程度大于$ϵ$-的个体，则认为解是不可行的。$ϵ$-Constraint方法的关键是$ϵ$的值。已经设置好了。在[12]中，算法根据当前种群中可行解占总解数的比例动态调整$ϵ$的取值，适用于不可行域较大的CMOP。在文[23]中，通过设置不同的$ϵ$在不同时间取值，以平衡收敛性、多样性和可行性。在[48]中，如果种群的可行比例小于阈值$\alpha$，则$ϵ$的值逐渐减小，否则将其设置为种群个体间的最大约束违反程度，并提出了一种检测和逃逸策略，帮助种群摆脱局部最优。
  第三类是多对象化方法。其思想是将约束视为附加目标，将约束优化问题转化为多目标优化问题。文献[2]提出了一种可行比控制技术，并将其与多目标方法相结合，使搜索可行域与不可行域达到了较好的平衡。在[47]中，提出了一个三目标进化框架，该框架设计了收敛、多样性和解决约束多目标问题的可行性三个指标。
  最后一类是杂交法。该方法结合了多种不同的约束处理技术来处理约束问题。在[42]中，提出了一种自适应权衡模型，将种群演化过程分为三种情况，即种群中只有可行解、种群中只有不可行解、种群中既有可行解又有不可行解。在[42]中，针对不同的进化情况设计了不同的个体比较和选择标准。在[22]中，针对环境选择问题设计了一种新型的选择进化策略。首先，从整个父代和子代种群中剔除违反约束较大的个体，并选择所有非劣势个体来获得下一代。然后，如果非劣势个体的数量小于种群规模，则使用惩罚函数方法来选择剩余的个体。
  近年来，也发展了一些多阶段或多种群的CMOEA来解决CMOP问题。在文[31]中，提出了一个求解带有欺骗约束的CMOP问题的两阶段协同进化框架。第一阶段采用两个子群：一个用于探索可行区域，另一个用于探索整个空间。第二阶段以这两个子种群为初始种群，寻找Pareto最优解。这两个阶段可以根据进化过程中发现的信息进行切换。在[14]中，提出的PPS框架将搜索过程分为两个不同的阶段：推和拉搜索阶段。在推的阶段，采用多目标进化算法搜索搜索空间，不考虑任何约束条件，快速穿越不可行域，逼近无约束的Pareto前沿。在拉的阶段，考虑了这些约束条件，以帮助种群回到真正的帕累托前沿。在[27]中，还提出了一个称为ToP的两阶段框架。首先，第一阶段只考虑单目标和所有约束，从而将原始的CMOP问题转化为有约束的单目标优化问题来寻找最有希望的可行域。然后，在第二阶段，考虑所有的约束和目标，以获得最终的解。在[39]中，提出了一种两阶段进化算法，在进化过程中调整适应度评估策略，以自适应地平衡目标优化和约束满足。在第一阶段，目标对到达所有可行域的约束给予相同的优先级。在第二阶段，目标优先于沿着可行边界使解决方案多样化的约束条件。在[41]中，提出了一种用于约束多目标优化的协作DE框架CCMODE，该框架包括用于约束单目标优化的M个子种群和用于约束M目标优化的档案种群。在文献[25]中，提出了一种求解约束多目标优化问题的两档进化算法C-TAEA。面向收敛的档案(CA)旨在优化约束和目标，旨在将种群推向帕累托前沿，而面向多样性的档案(DA)则进化为优化目标，旨在探索CA未充分开发的区域，包括不可行的区域。CCMO[38]也是一种进化算法，它进化两个种群。该框架通过进化一个种群来解决原CMOP问题，以保持可行性和收敛，同时进化另一个种群来解决由原问题衍生的辅助问题，以保持多样性。

2.2 写作动机

  尽管已有许多约束多目标进化算法被用于求解CMOP问题，并取得了很好的效果，但大多数算法在处理复杂约束的CMOP问题时面临困难。通常，现有的大多数约束优化问题都有多个约束[27，12]，这些不同的约束协同形成一个复杂的约束景观。例如，可行区域可以是狭窄和离散的，也可以是巨大的不可行障碍。

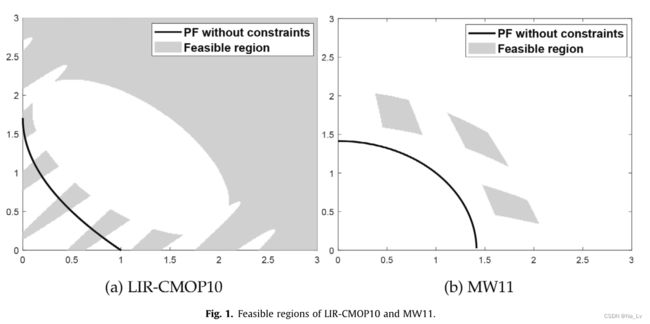
  基于已有算法的对比，我们有两个重要的观察结果：首先，一个狭窄的可行域会给寻找可行方案带来困难。其次，离散的可行域会导致局部最优。但是，如果单独处理前面提到的复杂约束，它们就不再被认为是复杂的。基于这种思想，本文逐一考虑约束条件，将求解CMOP问题的过程分成多个阶段。具体而言，该算法从只处理一个约束开始，然后在每个阶段逐步考虑更多的约束。这样，就可以很容易地解决原来复杂的CMOPS问题。在下一节中，将描述拟议的MSCMO的程序。

3 The proposed algorithm

3.1 MSCMO的概述

总流程伪代码：
输入：$n$(种群大小)、$\lambda$(阶段变换的阈值参数)、$Archive$(储存解的外部档案)
输出：$P$(最终种群)
首先，决定约束条件的优先顺序：
$CHP=Constraint\_Priority\_Determinate(n,\lambda )$
种群初始化：
最初种群记为$P$；
当前阶段的约束条件记为$currentConstraint$；
种群的适应度为：$F$(这里及以下所有适应度的计算方法采用SPEA2中的方法)
开始循环直至达到最大迭代次数：
 繁殖
基于适应度用二进制锦标赛的方法从$P$中选出$n$个亲代记为$P^{\prime }$
由亲代产生的子代记为$Offspring$
$Offspring$与$P$共同组成新的$P$
 更新外部档案
如果$\left|currentConstraint\right|>0$，则
从$Offspring\cup Archive$中选择满足约束条件的非支配解储存到$Archive$中
 环境选择
计算此时种群$P$的适应度$F$。
根据适应度利用截断方法从$P$中选择$n$个解记为$P$。
 决定是否进入下一阶段
若$\left|currentConstraint\right|=0$(说明当前是第一阶段)
种群在最高优先级的约束条件下不可行解的比例记为$ifr$
  若$ifr>0$
  则进入下一阶段：加入下一优先级（最高优先级）的约束条件并重新计算种群适应度
否则$\left|currentConstraint\right|>0$(不是第一阶段)
计算种群在每个目标函数上的均值改变量，并记最大值为$maxChange$
  若$maxChange\le \lambda$
  则进入下一阶段：加入下一优先级的约束条件并且重新计算种群的适应度
  构建下一阶段的初始种群
  若$\left|Archive\right|=n$，则$Archive=P$；
  若$\left|Archive\right|>n$，则参照SPEA2中的截断方法；
  若$\left|Archive\right|<n$，则参照C-TAEA中的DA的更新方法。
输出最终的种群$P$

$Constraint\_Priority\_Determinate$伪代码
输入：$n$(种群大小)、$\lambda$(阶段变换的阈值参数)
输出：$CHP$
随机初始化的种群记为$P_1$
根据$P_1$可以得到对约束条件优先级的排序$CHP$
计算$P_1$中个体对应的适应度$F_1$
以下循环直至达到最大迭代次数
 使用二进制锦标赛方法¹根据适应度从$P_1$中选择$n$个亲代组成$P_1^{\prime }$
 $P_1$与$P_1^{\prime }$的子代重新组成$P_1$
 重新计算$P_1$的适应度$F_1$
 用截断法从$P_1$中选出$n$个解组成$P_1$
 计算种群在每个目标函数上改变量，并记最大值为$maxChange$
 若$maxChange\le \lambda$
 计算种群在每个约束条件下的不可行率为$ifr$
 将不可行率按降序排列，将对应的约束条件排序储存到$CHP$中
输出$CHP$

3.2 算法中的关键技术

  在这一小节中，我们介绍了所提出的多阶段约束处理技术中的三个关键部分：每个阶段的种群重新初始化，每个阶段的适应度评估，以及从当前阶段到下一阶段的转换条件。
  每阶段的种群初始化 需要注意在多阶段进化算法中，每个阶段都要借助之前储存在外部档案中的解重新初始化种群。若$\left|Archive\right|=n$，则$Archive=P$；若$\left|Archive\right|>n$，则参照SPEA2中的截断方法²；若$\left|Archive\right|<n$，则参照C-TAEA中的DA的更新方法。
  每阶段的适应度计算 使用SPEA2中适应度的计算方法。此外，为了使算法达到更好的性能，我们在不同的阶段使用了不同的约束处理机制。具体地说，在进化的早期阶段，使用基于多目标优化的约束处理机制来处理约束，以获得具有良好多样性的解，其中将当前阶段的约束违反程度作为额外的目标函数，并使用SPEA2中的方法来计算适应值。在最后阶段，综合考虑所有约束条件，采用了基于可行性规则的约束处理机制来加速收敛。
  当前阶段转换为下一阶段的条件 如果是第一阶段，则只需要判断当前约束下解集的不可行率大于零，即可进入下一阶段，在后续阶段更新过程中，需要判断种群在每个目标上的变化平均值小于给定的阈值$\lambda$时（本文中取$\lambda =0.01$），才能进入下一阶段。第$i$个目标函数上的变化平均值计算方式如下：
$$\begin{array}{rl}& f_i^{\prime }\left(\mathbf{x}\right)=\frac{f_i\left(\mathbf{x}\right)-f_i^{\min }}{f_i^{\max }-f_i^{\min }}\\ & \overline{f_i^{\prime }}=\frac{{\sum }_{\mathbf{x}\in P}{f}_i^{\prime }\left(\mathbf{x}\right)}{\left|P\right|}\end{array}$$这里$f_i^{\max }$、$f_i^{\min }$表示种群中关于第$i$个目标函数的最大值和最小值。

3.3 对MSCMO的分析

4 Experimental study

5 Conclusion

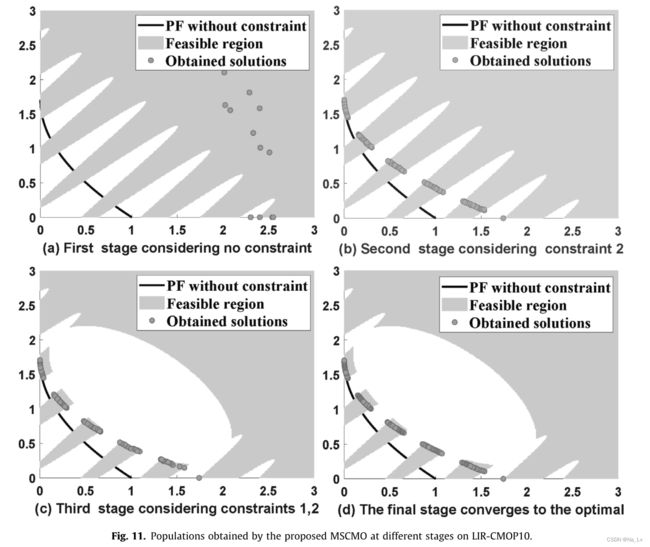
  本文提出了一种求解具有相对复杂可行域的CMOPS的多阶段CMOEA算法。具体地说，在该算法中，约束是逐个添加的，并在不同的进化阶段进行处理。在算法的早期阶段，只考虑了少量的约束条件，使种群高效地收敛到具有良好多样性的潜在可行域。当算法进入下一阶段时，考虑了更多的约束条件，并通过使用前一阶段的解来保持种群的多样性。这样，原来复杂的问题就迎刃而解了。此外，我们还对约束进行排序和组合，以提高搜索可行解的效率和收敛速度。在实验部分，将提出的算法与几种最先进的CMOEA算法在五个基准测试套件和三个真实应用程序上进行了比较。结果表明，我们提出的算法具有很强的竞争力，特别是对于具有复杂约束的CMOP。
  由于该算法具有很强的灵活性和易于实现的特点，因此该算法也适用于求解其他类型的可行域较复杂的CMOP问题。此外，为约束设计更有效的排序和组合策略，以进一步提高效率和效果也是有趣的。例如，我们可以对约束类型进行分类，并一起处理相同类型的约束。

References

[2] R. Jiao, S. Zeng, C. Li, A feasible-ratio control technique for constrained optimization, Information Sciences 502 (2019) 201–217.
[7] K. Deb, An efficient constraint handling method for genetic algorithms, Computer Methods in Applied Mechanics and Engineering 186 (2000) 311–338.
[11] K. Deb, A. Pratap, S. Agarwal, T. Meyarivan, A fast and elitist multiobjective genetic algorithm: NSGA-II, IEEE Transactions on Evolutionary Computation 6 (2002) 182–197.
[12] Z. Fan, W. Li, X. Cai, H. Huang, Y. Fang, Y. You, J. Mo, C. Wei, E.D. Goodman, An improved epsilon constraint-handling method in moea/d for cmops with large infeasible regions, Soft Computing 23 (2019) 12491–12510…
[14] Z. Fan, W. Li, X. Cai, H. Li, C. Wei, Q. Zhang, K. Deb, E.D. Goodman, Push and pull search for solving constrained multi-objective optimization problems, Swarm and Evolutionary Computation 44 (2019) 665–679.
[15] R. Farmani, J.A. Wright, Self-adaptivefitness formulation for constrained optimization, IEEE Transactions on Evolutionary Computation 7 (2003) 445– 455, https://doi.org/10.1109/TEVC.2003.817236.
[18] A. Homaifar, C. Qi, H.Y. Lai, Constrained optimization via genetic algorithms, Transactions of The Society for Modeling and Simulation International -SIMULATION 62 (1994) 242–253, https://doi.org/10.1177/003754979406200405.
[19] Z. Hou, C. He, R. Cheng, Reformulating preferences into constraints for evolutionary multi- and many-objective optimization, Information Sciences 541 (2020) 1–15…
[22] L. Jiao, L. Li, R. Shang, F. Liu, R. Stolkin, A novel selection evolutionary strategy for constrained optimization, Information Sciences 239 (2013) 122–141.
[23] R. Jiao, S. Zeng, C. Li, S. Yang, Y.S. Ong, Handling constrained many-objective optimization problems via problem transformation, IEEE Transactions on Cybernetics (2020) 1–14, https://doi.org/10.1109/TCYB.2020.3031642.
[24] B. Li, K. Tang, J. Li, X. Yao, Stochastic ranking algorithm for many-objective optimization based on multiple indicators, IEEE Transactions on Evolutionary Computation 20 (2016) 924–938.
[25] K. Li, R. Chen, G. Fu, X. Yao, Two-archive evolutionary algorithm for constrained multi-objective optimization, IEEE Transactions on Evolutionary Computation 23 (2018) 303–315.
[26] Chih-Hao Lin, A rough penalty genetic algorithm for constrained optimization, Information Sciences 241 (2013) 119–137.
[30] J.R. McDonnell, R.G. Reynolds, D.B. Fogel, A Survey of Constraint Handling Techniques in Evolutionary Computation Methods, MIT Press, 1995.
[31] C. Peng, H. Liu, E.D. Goodman, A cooperative evolutionary framework based on an improved version of directed weight vectors for constrained multiobjective optimization with deceptive constraints, IEEE Transactions on Cybernetics (2020) 1–13.
[34] Y. Qi, X. Ma, F. Liu, L. Jiao, J. Sun, J. Wu, MOEA/D with adaptive weight adjustment, Evolutionary Computation 22 (2014) 231–264.
[35] C. Saha, S. Das, K. Pal, S. Mukherjee, A fuzzy rule-based penalty function approach for constrained evolutionary optimization, IEEE Transactions on Cybernetics 46 (2016) 2953–2965, https://doi.org/10.1109/TCYB.2014.2359985.
[36] Y. Tian, R. Cheng, X. Zhang, F. Cheng, Y. Jin, An indicator-based multiobjective evolutionary algorithm with reference point adaptation for better versatility, IEEE Transactions on Evolutionary Computation 22 (2018) 609–622.
[37] Y. Tian, R. Cheng, X. Zhang, Y. Jin, PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [educational forum], IEEE Computational Intelligence Magazine 12 (2017) 73–87, https://doi.org/10.1109/MCI.2017.2742868.
[38] Y. Tian, T. Zhang, J. Xiao, X. Zhang, Y. Jin, A coevolutionary framework for constrained multi-objective optimization problems, IEEE Transactions on Evolutionary Computation (2020) 1, https://doi.org/10.1109/TEVC.2020.3004012.
[39] Y. Tian, Y. Zhang, Y. Su, X. Zhang, K. Tan, Y. Jin, Balancing objective optimization and constraint satisfaction in constrained evolutionary multi-objective optimization, IEEE Transactions on Cybernetics (2020), https://doi.org/10.1109/TCYB.2020.3021138.
[41] J. Wang, G. Liang, J. Zhang, Cooperative differential evolution framework for constrained multiobjective optimization, IEEE Transactions on Cybernetics 49 (2019) 2060–2072, https://doi.org/10.1109/TCYB.2018.2819208.
[42] Y. Wang, Z. Cai, Y. Zhou, W. Zeng, An adaptive tradeoff model for constrained evolutionary optimization, IEEE Transactions on Evolutionary Computation 12 (2008) 80–92.
[45] M. Zhang, W. Luo, X. Wang, Differential evolution with dynamic stochastic selection for constrained optimization, Information Sciences 178 (2008) 3043–3074.
[46] Q. Zhang, H. Li, MOEA/D: A multiobjective evolutionary algorithm based on decomposition, IEEE Transactions on Evolutionary Computation 11 (2007) 712–731.
[47] Y. Zhou, M. Zhu, J. Wang, Z. Zhang, Y. Xiang, J. Zhang, Tri-goal evolution framework for constrained many-objective optimization, IEEE Transactions on Systems, Man, and Cybernetics: Systems 50 (2020) 3086–3099, https://doi.org/10.1109/TSMC.2018.2858843.
[48] Q. Zhu, Q. Zhang, Q. Lin, A constrained multiobjective evolutionary algorithm with detect-and-escape strategy, IEEE Transactions on Evolutionary Computation (2020) 1.
[49] E. Zitzler, S. Kunzli, Indicator-based selection in multiobjective, search (2004) 832–842…
[50] E. Zitzler, M. Laumanns, L. Thiele, SPEA2: Improving the strength Pareto evolutionary algorithm for multiobjective optimization, in: Proceedings of the
Fifth Conference on Evolutionary Methods for Design, Optimization and Control with Applications to Industrial Problems, 2001, pp. 95–100.

---

1. 二进制锦标赛方法：每次从种群中任选2个个体竞争，选择获胜者，重复$n$次即可得到$n$个parents。 ↩︎

2. 见跳转链接后绿色字体。 ↩︎