2,4(1H,3H)-PD are mine

CodeTON Round 4 (Div. 1 + Div. 2, Rated, Prizes!)A~E

比赛连接：Dashboard - CodeTON Round 4 (Div. 1 + Div. 2, Rated, Prizes!) - Codeforces

A. Beautiful Sequence

题意：

t(1≤t≤500)组测试每组给定大小为n(1≤n≤100) 的序列，判断它是否存在一个子序列是好序列。一个序列是好序列当且仅当至少存在一个ai=i。

思路：

考虑到从原序列抽取一些数形成的子序列下标i只可能比原来小，如果原来存在一个i>=a[i]，存在一种选择方法使得子序列下标i减小到a[i]，否则不可能构造出来。

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include
#include
#include 
#include 
#define pii pair
#define pll pair
#define pil pair
#define pli pair
#define pdd pair
#define se second 
#define fi first
#define endl '\n'
#define rep(i,a,b) for (register int i=a;ib;--i)
#define MEM(a,x) memset(a,x,sizeof(a))
#define all(x) (x).begin(),(x).end()
#define M(x) ((x)%MOD)
#define db double
#define eps 1e-9
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
const int MOD=1e9+7;
const db pi=acos(-1.0);
const int N=110,M=2*N;
int a[N];
inline void solve()
{
	int n;
	cin>>n;
	rep(i,1,n+1) cin>>a[i];
	rep(i,1,n+1){
		if(i>=a[i]){
			cout<<"YES"<>_;
	while(_--){
		solve();
	}
	return 0;
}

B. Candies

题意：

t(1≤t≤1e4)组测试每组给定n(2≤n≤1e9) ，有两种操作，第一种是将x变为2*x-1，第二种是将x变为2*x+1，输出将1变为n的操作序列，最多不超过40次。

思路：

操作后的数只能变为奇数，故n为偶数时一定不能构造。n为奇数，考虑如何使n变为1，如果把n写为二进制形式，第一种逆操作相当于将n加一再右移一位，第二种为将n减一再右边移动一位，所以可以找到一种操作：每一次看n的最后两位，如果是11做第二种操作，这样就除去了最后一位，如果是01做第一种操作（不能做第二种操作，因为过程中不能出现偶数）。n的最大是1e9，最多30位，一定符合要求。

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include
#include
#include 
#include 
#define pii pair
#define pll pair
#define pil pair
#define pli pair
#define pdd pair
#define se second 
#define fi first
#define endl '\n'
#define rep(i,a,b) for (register int i=a;ib;--i)
#define MEM(a,x) memset(a,x,sizeof(a))
#define all(x) (x).begin(),(x).end()
#define M(x) ((x)%MOD)
#define db double
#define eps 1e-9
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
const int MOD=1e9+7;
const db pi=acos(-1.0);
const int N=40,M=2*N;
int a[N],b[N];
inline void solve()
{
	int n;
	cin>>n;
	if(n&1){
		int len=0,sz=0;
		while(n){
			a[++len]=n&1;
			n>>=1;
		}
		cout<>_;
	while(_--){
		solve();
	}
	return 0;
}

C. Make It Permutation

题意：

给定一个序列，可以进行两种操作，删除一个元素，花费为c，添加一个元素，花费为d，求使序列变为一个非空排列的最小花费。

思路：

因为排列不会存在重复元素，遇到重复元素一定要删除。将处理后的数组排序，考虑构造出1~a[i]的排列，删除后面的元素的花费，所有情况取最小值。注意将数组删除为空再补1的情况也要算。

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include
#include
#include 
#include 
#define pii pair
#define pll pair
#define pil pair
#define pli pair
#define pdd pair
#define se second 
#define fi first
#define endl '\n'
#define rep(i,a,b) for (register int i=a;ib;--i)
#define MEM(a,x) memset(a,x,sizeof(a))
#define all(x) (x).begin(),(x).end()
#define M(x) ((x)%MOD)
#define db double
#define eps 1e-9
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
const int MOD=1e9+7;
const db pi=acos(-1.0);
const int N=1e5+10,M=2*N;
int a[N],len;
inline void solve()
{
	len=0;
	setst;
	int n,c,d,x;
	LL ans=0;
	cin>>n>>c>>d;
	rep(i,1,n+1){
		cin>>x;
		if(st.count(x)) ans+=c;
		else st.insert(x),a[++len]=x;
	}
	sort(a+1,a+1+len);
	LL mi=1e18,tot=0;
	rep(i,1,len+1){
		tot+=a[i]-a[i-1]-1;
		mi=min(mi,tot*d+(LL)(len-i)*c);
	}
	mi=min(mi,(LL)len*c+d);
	cout<>_;
	while(_--){
		solve();
	}
	return 0;
}

D. Climbing the Tree

题意：

一个蜗牛爬树，树的高度为h，蜗牛每天爬a，下降b（a>b），从高度0花费n天爬上高度h。现在不知道h的值，有两种事件，事件1是给定a,b,n，需判断当前事件是否和前面的冲突；时间2是给定a,b，判断是否能根据当前信息求出确切的n。

思路：

先寻找a,b,h,n的关系，因为最后一次距离顶端小于等于a可以直接上去，考虑爬高度h-a的情况，显然需要 $\left \lceil \frac{h-a}{a-b} \right \rceil$ 天，最后再花一天爬上h，总天数为 $\left \lceil \frac{h-a}{a-b} \right \rceil+1$

对于事件1，有：

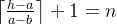
$\left \lceil \frac{h-a}{a-b} \right \rceil+1=n$

于是可以根据a,b,n的值算出h的下界和上界，分别用lh和rh表示：

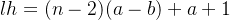
将lh和rh和前面的取交集，如果为空说明不合法，否则合法。

对于事件2，根据当前lh和rh可以根据上式计算出n，n唯一则说明有解，否则无解。

注意h<=a,n=1的边界情况。

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include
#include
#include 
#include 
#define pii pair
#define pll pair
#define pil pair
#define pli pair
#define pdd pair
#define se second 
#define fi first
#define endl '\n'
#define rep(i,a,b) for (register int i=a;ib;--i)
#define MEM(a,x) memset(a,x,sizeof(a))
#define all(x) (x).begin(),(x).end()
#define M(x) ((x)%MOD)
#define db double
#define eps 1e-9
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
const int MOD=1e9+7;
const db pi=acos(-1.0);
const int N=1e5+10,M=2*N;
int n;
void cal(int a,int b,LL &lh,LL &rh)
{
	if(n==1){
		lh=1,rh=a;
		return;
	}
	LL t=1ll*(n-2)*(a-b)+a;
	lh=t+1,rh=t+a-b;
}
LL calc(int a,int b,LL h)
{
	if(h<=a) return 1;
	LL res=(h-a)/(a-b);
	if((h-a)%(a-b)) res+=2;
	else res+=1;
	return res;
}
inline void solve()
{
	LL lh=-1,rh=1e18;
	int q;
	cin>>q;
	rep(_,0,q){
		int op,a,b;
		cin>>op>>a>>b;
		if(op==1){
			cin>>n;
			if(_){
				LL l,r;
				cal(a,b,l,r);
				if(l>rh||r>_;
	while(_--){
		solve();
	}
	return 0;
}

E. Monsters

题意：

给定一个n个点，m条边的无向无环图，每个点都有一个怪物对应一个危险值，能打败某个点的怪物当且仅当打败的怪物数大于等于危险值。开始选择一个点出发，可以通过一个点需要能打败该点的怪物，判断能否打败所有怪物。

n, m (1≤n,m≤2e5)

思路：

本题官方给出了最暴力的做法：找到每一个ai=0的点做扩散，每一次扩散判断是否能扩展到所有点。虽然直觉上会超时，但是可以证明这样做复杂度为O(n*log(n)*log(n))。

相比官方做法更容易想到用并查集维护连续可走的块。先将危险值从小到大排序，需要一个数组来记录一个集合是否被选择（是否走过），每一次扩散都将危险值大的点并到危险值小的点，维护集合大小，最后合法的结果是一定只有一个根节点。

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include
#include
#include 
#include 
#define pii pair
#define pll pair
#define pil pair
#define pli pair
#define pdd pair
#define se second 
#define fi first
#define endl '\n'
#define rep(i,a,b) for (register int i=a;ib;--i)
#define MEM(a,x) memset(a,x,sizeof(a))
#define all(x) (x).begin(),(x).end()
#define M(x) ((x)%MOD)
#define db double
#define eps 1e-9
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
const int MOD=1e9+7;
const db pi=acos(-1.0);
const int N=2e5+10,M=2*N;
pii p[N];
int h[N],e[M],ne[M],idx,s[N],d[N],ok[N],vis[N],sz[N];
void add(int a,int b)
{
	e[++idx]=b,ne[idx]=h[a],h[a]=idx;
}
int find(int x)
{
	if(x==s[x]) return s[x];
	return s[x]=find(s[x]);
}
inline void solve()
{
	idx=0;
	MEM(h,0);
	int n,m;
	cin>>n>>m;
	rep(i,1,n+1) cin>>p[i].fi,p[i].se=i,s[i]=i,ok[i]=0,vis[i]=0,sz[i]=1;
	sort(p+1,p+1+n);
	rep(i,0,m){
		int a,b;
		cin>>a>>b;
		add(a,b),add(b,a);
	}
	rep(_,1,n+1){
		int u=p[_].se;
		if(p[_].fi==0) ok[u]=1;
		vis[u]=1;
		for(int i=h[u];i;i=ne[i]){
			int v=e[i];
			if(!vis[v]) continue;
			u=find(u),v=find(v);
			if(sz[v]>=p[_].fi&&ok[v]) ok[u]=1;
			if(u!=v){
				sz[u]+=sz[v];
				s[v]=u;
			}
		}
	}
	if(!ok[find(1)]){
		cout<<"NO"<>_;
	while(_--){
		solve();
	}
	return 0;
}

E题补充说明：

几个数组代表的意义：

vis[i]: i在前面有没有走过，这个作用是保证在无向图中从危险值小的到危险值大的走。

ok[i]: i的块是否合法。

s[i]: 并查集i的根

sz[i]：i的块走过的个数，用于和危险值比较判断是否合法。

首先出发点一定是危险值尽量越小越好，我们考虑从危险值小的点走向危险值大的点，将所有点按照危险值小的到危险值大的排序。然后枚举，比如我们枚举到了u，然后遍历它的邻接点v，需要保证v是否前面遍历过（v的危险值小于等于u的危险值），第69行代码就是判断u这个点是否满足题目条件，最后将v并到u。

私信的一些问题：

Q1:为什么合并的时候不需要判断？

A1:因为这里用并查集只是为了维护一个点可以走到的点数，判断合法用ok数组另加判断。

Q2:并查集根节点代表什么？

A2:根节点为一个连通块危险值最大的点，它的ok的值代表了这个块是否合法。

Q3:为什么危险值为0的时候将ok的值置为1，危险值为1的时候为什么不可以。

A3:题目要求是当前打败的怪物数量大于等于当前点危险度，所以开始打败数量为0，当然危险值也是0。后面的判断也是当前走了的点大于等于危险值。

你可能感兴趣的:(codeforces刷题,codeforces,CodeTON)

java题库app有什么,Java面试题库 m0_74824091 面试学习路线阿里巴巴 java 面试开发语言
Java面试题库是一个学习刷题类软件，主要针对Java从业者设计，整合了众多基础的题目资源，涵盖面试中可能会遇到的各种出题内容；软件使用功能非常简单，上面就设置了题库和搜索等中心，打开软件就能看到其中各种不同的题目划分栏目，马上就能从推荐栏目找到需要练习的题目并打开练习学习，里面每个题目都提供相应的详细解释和对应的知识点击内容，让用户能高效的掌握该问题考察的考点信息；这里的题库资源丰富，还按照多种
二叉树-左叶子之和 Hasno. 深度优先算法
代码随想录-刷题笔记404.左叶子之和-力扣（LeetCode）内容：该题仅作为搜索，但是其中的规则让人摸不着头脑，看起来似乎很头疼但是仔细一思考，能发现左叶子无非是这样的定义当发现一个节点的左孩子不为null,并且左孩子的左右孩子都为null(叶子结点)那么可以知道，找到了左叶子OK，接下来就是常规的搜索,只要搜索到满足这样的节点，直接加到一个全局变量就OK了/***Definitionfora
二叉树-二叉树的所有路径 Hasno. 深度优先算法
代码随想录-刷题笔记257.二叉树的所有路径-力扣（LeetCode）内容：本题是一道递归+回溯的问题,其实递归和回溯是一个意思，但是这道题一定要明显的进行一次回溯。毕竟每一条路径都不太一样，收集完一次结果之后，需要把上一次探的节点给撤销.这一步就是很明显回溯回溯部分在回溯篇章再去详细写一篇笔记,因此本文只做介绍,至于路径问题,真可谓是回溯的常客了.哦，对每次都想吐槽一下Java的神奇的字符串,必
刷题记录4---二叉树的中序遍历+对称二叉树+二叉树的最大深度+翻转二叉树+二叉树的直径热巴的小哥哥算法和数据结构数据结构算法
前言所有题目均来自力扣题库中的hot100，之所以要记录在这里，只是方便后续复习94.二叉树的中序遍历题目：给定一个二叉树的根节点root，返回它的中序遍历。示例1：输入：root=[1,null,2,3]输出：[1,3,2]示例2：输入：root=[]输出：[]示例3：输入：root=[1]输出：[1]解题思路：【递归】中序遍历即先遍历左节点，再遍历根节点，最后遍历右节点；可采用递归的方法，也可
洛谷 CF2022A：Bus to Pénjamo ← 模拟题 hnjzsyjyj 信息学竞赛 #模拟算法与基础语法算法
【题目来源】https://www.luogu.com.cn/problem/CF2022Ahttps://codeforces.com/contest/2022/problem/A【题目描述】有n个家庭前往佩恩哈莫，见证墨西哥有史以来最大规模的"拴着绳子遛鸡"马拉松比赛。其中i个家庭有ai名家庭成员。所有家庭将乘坐一辆大巴，每辆大巴有r排，2个座位。一个人在以下情况下被认为是幸福的：●另一名家庭
【leetcode刷题版】哈希表学废了wuwu leetcode 算法 python 哈希算法
系列文章目录文章目录系列文章目录背景知识一、有效的字母异位词二、两个数组的交集三、快乐数四、两数之和五、四数相加六、赎金信七、三数之和八、四数之和背景知识哈希函数（HashFunction）：哈希函数是一种将任意长度的输入（键）通过某种算法转换为固定长度的输出（哈希值）的函数。好的哈希函数应该能够将输入均匀地分布在哈希表中，以减少冲突。冲突（Collision）：当两个不同的键通过哈希函数得到相同
【leetcode刷题版】回溯算法学废了wuwu 算法 leetcode python
系列文章目录文章目录系列文章目录背景知识一、组合二、组合优化三、电话号码的字母组合四、组合总和五、组合总和Ⅱ六、分割回文串七、复原IP地址八、子集九、子集（需要去重）十、非递减子序列十一、全排列十一、全排列Ⅱ十二、重新安排行程（难）十三、N皇后十四、解数独背景知识回溯算法是一种通过试错来解决问题的算法。它会在解决问题的过程中剪枝，以避免无效搜索。在Python中实现回溯算法通常涉及以下几个步骤：定
刷力扣的技巧：4 个步骤 7 个关键点，事半功倍，冲进大厂！后端go数据库算法力扣
最近好多人问我咋刷力扣呀，今天我就来给大家好好唠唠。我总结了7个要点和4个步骤，尤其是最后那提效4步骤，可太有用啦。大家一定要看到最后哦，记得点赞、收藏呀。要点一：别光追求刷题量，题解也得看咱好多同学呀，解开一道题就着急忙慌地去刷下一道，还把刷题数量当成衡量水平的唯一标准。就像有的同学跟我说：“阳哥，我在Leetcode刷了500题，去面腾讯有戏不？”结果咋样，还不是挂了。其实呀，咱不能光闷头刷，
二叉树-二叉树的最大深度 Hasno. java 算法
代码随想录-刷题笔记104.二叉树的最大深度-力扣（LeetCode）内容:本题较为基础,可以说是深搜的入门款，深搜的具体知识点请看图论-表示形式&深度优先搜索-CSDN博客这篇文章当然二叉树肯定不会跟通用的深搜模板一样那么复杂，只需要处理左右两个子树即可.对于二叉树分为三种遍历方式二叉树的前序遍历求深度-深度是从根节点开始算，一直到叶子节点二叉树的后序遍历求高度-高度是从叶子节点开始算，一直到根
力扣刷题 1. 两数之和 weixin_43103920 力扣 leetcode python
力扣1.两数之和题目第一次回答结果优化后代码结果分析总结题目给定一个整数数组nums和一个整数目标值target，请你在该数组中找出和为目标值target的那两个整数，并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案。示例1：输入：nums=[2,7,11,15],target=9输出：[0,1]解释：因为nums[0]
括号配对问题【刷题反思】 wanjiazhongqi 刷题反思栈 c++数据结构
1.判断括号配对1.1题目题目描述：给定一个只包括'(',')','{','}','[',']'的字符串s，判断字符串是否有效有效字符串：1.左括号必须用相同类型的右括号闭合2.左括号必须以正确的顺序闭合3.每个右括号都有⼀个对应的相同类型的左括号示例：输入：s="()[]{}"输出：trueclassSolution{public:boolisValid(strings){}};1.2思想栈的“
【华为OD机试真题E卷】1、滑动窗口最大值 | 机试真题+思路参考+代码解析（C++、Java、Py） KFickle Java Py）华为od c++java 华为OD机试真题滑动窗口最大值
文章目录一、题目题目描述输入输出样例1样例2二、代码与思路参考C++代码Java代码Python代码订阅本专栏后即可解锁在线OJ刷题权限个人博客首页：KFickle专栏介绍：最新的华为OD机试真题D、E卷，每题都使用C++，Java，Python语言进行解答，每个题目的思路分析都非常详细，持续更新，支持在线OJ刷题，订阅后评论获取权限，有代码问题随时解答，代码仅供学习参考一、题目题目描述有一个N个
LeetCode刷题之道 cook_1996 算
本文作者：侯振宇，原文链接：https://www.cnblogs.com/sskyy/p/8268976.html这篇文章最早发在我团队的文档中。我的团队鼓励每个同学都在业余时间多做算法题，特别是新人。个人认为在编程能力的提升上比做sideproject更有用，对职业发展也是如此。当然出于兴趣做的sideproject另当别论。转到这里，希望对各位读者有用。如何有效地写算法题目的持续做算法题的目
统计学基础知识点刷题（task2） sm376624607 统计学
参考视频：可汗学院《统计学》参考书籍：《深入浅出统计学》文章目录概念1:中心极限定理概念2:置信区间概念3:伯努利分布概念4:误差范围概念5:小样本容量置信区间概念1:中心极限定理核心内容：随着抽样次数趋于∞\infty∞,样本均值的抽样分布趋近于正态分布，且该正态分布的均值为总体均值。X‾服从N(μ,σ/n)\overline{X}服从N(\mu,\sigma/\sqrt{n})X服从N(μ,σ
日常整理系列——笔试刷题00002 Cutepingping 前端h5+css JavaScript语言笔试题库
1.RegExp对象的方法JavaScriptRegExp对象有3个方法：test()、exec()和compile()。(1)test()方法用来检测一个字符串是否匹配某个正则表达式，如果匹配成功，返回true，否则返回false；(2)exec()方法用来检索字符串中与正则表达式匹配的值。exec()方法返回一个数组，其中存放匹配的结果。如果未找到匹配的值，则返回null；（3）compile
日常知识点之刷题一 yun6853992 常用知识点 od刷题
1：流浪地球0~n-1个发动机，计划启动m次，求最后启动的发动机的个数。以及发动机的编号。（模拟过程，每次手动启动的机器对应时间向两边扩散）//输入每个启动的时间和编号voidtest_liulang(){intn,m;cin>>n>>m;if(n>1000||m>n){return;}intt,p;vector>vec;for(inti=0;i>t>>p;vec.push_back({t,p})
刷题统计（C语言） xinghuitunan 蓝桥杯 c语言
问题描述小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天做aa道题目,周六和周日每天做bb道题目。请你帮小明计算,按照计划他将在第几天实现做题数大于等于nn题?输入格式输入一行包含三个整数a,ba,b和nn.输出格式输出一个整数代表天数。样例输入102099样例输出8代码：#includeintmain(){//请在此输入您的代码inta,b,n,sum,d;scanf("%d%d
算法题刷题C++常用函数 zhihao_Guo 数据结构与算法算法 c++java
String字符串函数常见用法字符串倒置//方式1：#includereverse(str1.begin(),str1.end());//方式2：voidrevers(){intc=getchar();if(c!='\n')revers();putchar(c);}//方式1的reverse方法可以实现类似“China”字符串的倒置输出的，但是对于“Ilovemynation”的倒置输出就无能为力
二叉树-对称二叉树 Hasno. 算法
代码随想录-刷题笔记101.对称二叉树-力扣（LeetCode）内容:本题有一定的难度，但其实想明白需要同时用到左右节点之后，就没什么难度了本题是看左右是否对称，并非左右节点是否相等，相信仔细读过题不可能不明白这一点好了，接下来开始递归三部曲1.确定返回值和参数因为要返回trueorfalse,所以一定是bool类型,参数上面也提到一定要是左右节点publicbooleancompare(Tree
【刷题】贪心算法 llllliznc 贪心算法算法
贪心算法通常用于那些可以通过局部最优解达到全局最优解的问题，也就是说每一步都选择当前看起来最好的选项，从而希望最终的结果是最优的。基础概念[分配问题]：局部最优满足需求，排序后贪心分配分发饼干分发糖果[区间问题]：按区间右端点排序，最大化不重叠区间无重叠区间用最少数量的箭引爆气球经典贪心模型[跳跃问题]：维护最大覆盖范围，贪心选择下一步跳跃游戏跳跃游戏II[加油站问题]：总油量足够时，局部油量最低
华为OD最新机试真题-喊7的次数重排-C++-OD统一考试（E卷） ai因思坦华为od c++链表动态规划算法开发语言数据结构
最新华为OD机试考点合集：华为OD机试2024年真题题库（E卷+D卷+C卷）_华为od机试题库-CSDN博客每一题都含有详细的解题思路和代码注释，精选c++、JAVA、Python三种语言解法。帮助每一位考生轻松、高效刷题。订阅后永久可看，持续跟新。题目描述：喊7是一个传统的聚会游戏，N个人围成一圈，按顺时针从1到N编号。编号为1的人从1开始喊数，下一个人喊的数字为上一个人的数字加1，但是当将要喊
LeetCode刷题面试题39.数组中出现次数超过一半的数字 _深海凉_ LeetCode
题目要求：在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。分析：使用归并排序中分治思想，先将数组中数字递归划分，然后再合并进行排序同时统计逆序数。classSolution{public:intreverseCount=0;intreversePairs(vector&nums){if(nums.empty())retur
LeetCode热题100刷题12 Liwan95 LeetCode leetcode 算法职场和发展
23.合并K个升序链表给你一个链表数组，每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中，返回合并后的链表。与合并两个有序链表类似，但是需要在k个链表节点中找到最小的。考虑使用优先队列。classSolution{classStatusimplementsComparable{intval;ListNodenode;publicStatus(intval,ListNodenode){t
HDLBits刷题记录——Conwaylife Candy_579 verilog
导言HDLBits网站Morecircuits中的Conwaylife即Gameoflife，由数学家JohnConway创造。之所以特别关注到这个题目，是因为某位同学曾拿这个游戏作为一门芯片设计课程的PJ。当时觉得生命游戏在众多坦克大战、走迷宫等小游戏中挺有新意，其实现程度比这个题目本身要复杂很多，比如精美的GUI和复杂的场景。思路题目告诉我们，这个16×16的细胞网格是一个toroid，可以理
LeetCode Hot100刷题——最小路径和（动态规划）圈圈编码 leetcode 算法职场和发展动态规划 java
64.最小路径和给定一个包含非负整数的mxn网格grid，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。说明：每次只能向下或者向右移动一步。示例1：输入：grid=[[1,3,1],[1,5,1],[4,2,1]]输出：7解释：因为路径1→3→1→1→1的总和最小。示例2：输入：grid=[[1,2,3],[4,5,6]]输出：12提示：m==grid.lengthn==grid[
蓝桥与力扣刷题（蓝桥好数） এ旧栎 leetcode 算法职场和发展学习方法 java
题目：一个整数如果按从低位到高位的顺序，奇数位(个位、百位、万位⋯⋯)上的数字是奇数，偶数位(十位、千位、十万位⋯⋯)上的数字是偶数，我们就称之为“好数”。给定一个正整数N，请计算从1到N一共有多少个好数。输入格式一个整数N。输出格式一个整数代表答案。样例输入124样例输出17样例输入22024样例输出2150样例说明对于第一个样例，24以内的好数有1、3、5、7、9、21、23，一共7个。解题思
【找工作】Codefun刷题记录在雨中612 求职笔记
文章目录字节2024101320240929https://codefun2000.com/字节https://codefun2000.com/pset/672ec37d6f06d8fe4b28c33820241013https://codefun2000.com/p/P2181第2题-字典序题目有个坑是“恰好”。意味着即使已经是最优了，但是还没用完操作数，就必须再得操作一次，导致有可能不是最优的
1.python实现二分查找（力扣刷题）踏雪1352 leetcode 算法 python
二分查找（BinarySearch），也称为折半查找，是一种高效的查找算法，适用于在有序数组中查找特定元素。其基本思想是通过将查找范围逐步减半来快速定位目标值。题目力扣704题二分查找力扣35题搜索插入位置力扣34题在排序数组中查找元素的第一个和最后一个位置力扣69题x的平方根力扣367题有效的完全平方数1.力扣704题二分查找题目给定一个n个元素有序的（升序）整型数组nums和一个目标值targ
数据结构：动态数组vector 干炒牛河笔试笔记数据结构算法
vector是C++标准库的动态数组。在C语言中一般初学者会使用malloc，int[n]等方式来创建静态数组，但是这种方式繁琐且容易出错。我们做算法题一般使用动态数组vector，并且在刷题网站的题目给的输入一般也是vector类型。示例：vector的初始化如下：#includeintn=7,m=8;//初始化一个int型的空数组numsvectornums;//初始化一个大小为n的数组num
华为OD机试真题-相对开音节-OD统一考试（E卷） ai因思坦华为OD机试2024真题题库华为od 面试开发语言算法
最新华为OD机试考点合集：华为OD机试2024年真题题库（E卷+D卷+C卷）_华为od机试题库-CSDN博客每一题都含有详细的解题思路和代码注释，精编c++、JAVA、Python三种语言解法。帮助每一位考生轻松、高效刷题。订阅后永久可看，发现新题及时跟新。题目描述相对开音节构成的结构为:辅音+元音(aeiou)+辅音(r除外)+e。常见
集合框架天子之骄 java 数据结构集合框架
集合框架集合框架可以理解为一个容器，该容器主要指映射(map)、集合(set)、数组(array)和列表(list)等抽象数据结构。从本质上来说，Java集合框架的主要组成是用来操作对象的接口。不同接口描述不同的数据类型。简单介绍： Collection接口是最基本的接口，它定义了List和Set，List又定义了LinkLi
Table Driven（表驱动）方法实例 bijian1013 java enum Table Driven 表驱动
实例一： /** * 驾驶人年龄段 * 保险行业，会对驾驶人的年龄做年龄段的区分判断 * 驾驶人年龄段：01-[18,25);02-[25,30);03-[30-35);04-[35,40);05-[40,45);06-[45,50);07-[50-55);08-[55,+∞) */ public class AgePeriodTest { //if...el
Jquery 总结 cuishikuan java jquery Ajax Web jquery方法
1.$.trim方法用于移除字符串头部和尾部多余的空格。如：$.trim(' Hello ') // Hello2.$.contains方法返回一个布尔值，表示某个DOM元素（第二个参数）是否为另一个DOM元素（第一个参数）的下级元素。如：$.contains(document.documentElement, document.body); 3.$
面向对象概念的提出麦田的设计者 java 面向对象面向过程
面向对象中，一切都是由对象展开的，组织代码，封装数据。在台湾面向对象被翻译为了面向物件编程，这充分说明了，这种编程强调实体。下面就结合编程语言的发展史，聊一聊面向过程和面向对象。 c语言由贝尔实
linux网口绑定被触发 linux
刚在一台IBM Xserver服务器上装了RedHat Linux Enterprise AS 4，为了提高网络的可靠性配置双网卡绑定。一、环境描述我的RedHat Linux Enterprise AS 4安装双口的Intel千兆网卡，通过ifconfig -a命令看到eth0和eth1两张网卡。二、双网卡绑定步骤： 2.1 修改/etc/sysconfig/network
XML基础语法肆无忌惮_ xml
一、什么是XML？ XML全称是Extensible Markup Language，可扩展标记语言。很类似HTML。XML的目的是传输数据而非显示数据。XML的标签没有被预定义，你需要自行定义标签。XML被设计为具有自我描述性。是W3C的推荐标准。二、为什么学习XML？用来解决程序间数据传输的格式问题做配置文件充当小型数据库三、XML与HTM
为网页添加自己喜欢的字体知了ing 字体秒表 css
@font-face { font-family: miaobiao;//定义字体名字 font-style: normal; font-weight: 400; src: url('font/DS-DIGI-e.eot');//字体文件 } 使用： <label style="font-size:18px;font-famil
redis范围查询应用-查找IP所在城市矮蛋蛋 redis
原文地址： http://www.tuicool.com/articles/BrURbqV 需求根据IP找到对应的城市原来的解决方案 oracle表（ip_country）：查询IP对应的城市： 1.把a.b.c.d这样格式的IP转为一个数字，例如为把210.21.224.34转为3524648994 2. select city from ip_
输入两个整数，计算百分比 alleni123 java
public static String getPercent(int x, int total){ double result=(x*1.0)/(total*1.0); System.out.println(result); DecimalFormat df1=new DecimalFormat("0.0000%");
百合——————>怎么学习计算机语言百合不是茶 java 移动开发
对于一个从没有接触过计算机语言的人来说，一上来就学面向对象，就算是心里上面接受的了，灵魂我觉得也应该是跟不上的，学不好是很正常的现象，计算机语言老师讲的再多，你在课堂上面跟着老师听的再多，我觉得你应该还是学不会的，最主要的原因是你根本没有想过该怎么来学习计算机编程语言，记得大一的时候金山网络公司在湖大招聘我们学校一个才来大学几天的被金山网络录取，一个刚到大学的就能够去和
linux下tomcat开机自启动 bijian1013 tomcat
方法一：修改Tomcat/bin/startup.sh 为: export JAVA_HOME=/home/java1.6.0_27 export CLASSPATH=$CLASSPATH:$JAVA_HOME/lib/tools.jar:$JAVA_HOME/lib/dt.jar:. export PATH=$JAVA_HOME/bin:$PATH export CATALINA_H
spring aop实例 bijian1013 java spring AOP
1.AdviceMethods.java package com.bijian.study.spring.aop.schema; public class AdviceMethods { public void preGreeting() { System.out.println("--how are you!--"); } } 2.beans.x
[Gson八]GsonBuilder序列化和反序列化选项enableComplexMapKeySerialization bit1129 serialization
enableComplexMapKeySerialization配置项的含义 Gson在序列化Map时，默认情况下，是调用Key的toString方法得到它的JSON字符串的Key，对于简单类型和字符串类型，这没有问题，但是对于复杂数据对象，如果对象没有覆写toString方法，那么默认的toString方法将得到这个对象的Hash地址。 GsonBuilder用于
【Spark九十一】Spark Streaming整合Kafka一些值得关注的问题 bit1129 Stream
包括Spark Streaming在内的实时计算数据可靠性指的是三种级别： 1. At most once，数据最多只能接受一次，有可能接收不到 2. At least once, 数据至少接受一次，有可能重复接收 3. Exactly once 数据保证被处理并且只被处理一次，具体的多读几遍http://spark.apache.org/docs/lates
shell脚本批量检测端口是否被占用脚本 ronin47
#!/bin/bash cat ports |while read line do#nc -z -w 10 $line nc -z -w 2 $line 58422>/dev/null2>&1if[ $?-eq 0]then echo $line:ok else echo $line:fail fi done 这里的ports 既可以是文件
java-2.设计包含min函数的栈 bylijinnan java
具体思路参见：http://zhedahht.blog.163.com/blog/static/25411174200712895228171/ import java.util.ArrayList; import java.util.List; public class MinStack { //maybe we can use origin array rathe
Netty源码学习-ChannelHandler bylijinnan java netty
一般来说，“有状态”的ChannelHandler不应该是“共享”的，“无状态”的ChannelHandler则可“共享” 例如ObjectEncoder是“共享”的, 但 ObjectDecoder 不是因为每一次调用decode方法时，可能数据未接收完全（incomplete），它与上一次decode时接收到的数据“累计”起来才有可能是完整的数据，是“有状态”的 p
java生成随机数 cngolon java
方法一： /** * 生成随机数 * @author [email protected] * @return */ public synchronized static String getChargeSequenceNum(String pre){ StringBuffer sequenceNum = new StringBuffer(); Date dateTime = new D
POI读写海量数据 ctrain 海量数据
import java.io.FileOutputStream; import java.io.OutputStream; import org.apache.poi.xssf.streaming.SXSSFRow; import org.apache.poi.xssf.streaming.SXSSFSheet; import org.apache.poi.xssf.streaming
mysql 日期格式化date_format详细使用 daizj mysql date_format 日期格式转换日期格式化
日期转换函数的详细使用说明 DATE_FORMAT(date,format) Formats the date value according to the format string. The following specifiers may be used in the format string. The&n
一个程序员分享8年的开发经验 dcj3sjt126com 程序员
在中国有很多人都认为IT行为是吃青春饭的，如果过了30岁就很难有机会再发展下去!其实现实并不是这样子的，在下从事.NET及JAVA方面的开发的也有8年的时间了，在这里在下想凭借自己的亲身经历，与大家一起探讨一下。明确入行的目的很多人干IT这一行都冲着“收入高”这一点的，因为只要学会一点HTML, DIV+CSS，要做一个页面开发人员并不是一件难事，而且做一个页面开发人员更容
android欢迎界面淡入淡出效果 dcj3sjt126com android
很多Android应用一开始都会有一个欢迎界面，淡入淡出效果也是用得非常多的，下面来实现一下。主要代码如下： package com.myaibang.activity; import android.app.Activity;import android.content.Intent;import android.os.Bundle;import android.os.CountDown
linux 复习笔记之常见压缩命令 eksliang tar解压 linux系统常见压缩命令 linux压缩命令 tar压缩
转载请出自出处:http://eksliang.iteye.com/blog/2109693 linux中常见压缩文件的拓展名 *.gz gzip程序压缩的文件 *.bz2 bzip程序压缩的文件 *.tar tar程序打包的数据，没有经过压缩 *.tar.gz tar程序打包后，并经过gzip程序压缩 *.tar.bz2 tar程序打包后，并经过bzip程序压缩 *.zi
Android 应用程序发送shell命令 gqdy365 android
项目中需要直接在APP中通过发送shell指令来控制lcd灯，其实按理说应该是方案公司在调好lcd灯驱动之后直接通过service送接口上来给APP，APP调用就可以控制了，这是正规流程，但我们项目的方案商用的mtk方案，方案公司又没人会改，只调好了驱动，让应用程序自己实现灯的控制，这不蛋疼嘛！！！！发就发吧！一、关于shell指令：我们知道，shell指令是Linux里面带的
java 无损读取文本文件 hw1287789687 读取文件无损读取读取文本文件 charset
java 如何无损读取文本文件呢？以下是有损的 @Deprecated public static String getFullContent(File file, String charset) { BufferedReader reader = null; if (!file.exists()) { System.out.println("getFull
Firebase 相关文章索引 justjavac firebase
Awesome Firebase 最近谷歌收购Firebase的新闻又将Firebase拉入了人们的视野，于是我做了这个 github 项目。 Firebase 是一个数据同步的云服务，不同于 Dropbox 的「文件」，Firebase 同步的是「数据」，服务对象是网站开发者，帮助他们开发具有「实时」（Real-Time）特性的应用。开发者只需引用一个 API 库文件就可以使用标准 RE
C++学习重点 lx.asymmetric C++笔记
1.c++面向对象的三个特性：封装性，继承性以及多态性。 2.标识符的命名规则：由字母和下划线开头，同时由字母、数字或下划线组成；不能与系统关键字重名。 3.c++语言常量包括整型常量、浮点型常量、布尔常量、字符型常量和字符串性常量。 4.运算符按其功能开以分为六类：算术运算符、位运算符、关系运算符、逻辑运算符、赋值运算符和条件运算符。 &n
java bean和xml相互转换 q821424508 java bean xml xml和bean转换 java bean和xml转换
这几天在做微信公众号做的过程中想找个java bean转xml的工具，找了几个用着不知道是配置不好还是怎么回事，都会有一些问题，然后脑子一热谢了一个javabean和xml的转换的工具里，自己用着还行，虽然有一些约束吧，还是贴出来记录一下顺便你提一下下，这个转换工具支持属性为集合、数组和非基本属性的对象。 packag
C 语言初级位运算 1140566087 位运算 c
第十章位运算 1、位运算对象只能是整形或字符型数据，在VC6.0中int型数据占4个字节 2、位运算符：运算符作用 ~ 按位求反 << 左移 >> 右移 & 按位与 ^ 按位异或 | 按位或他们的优先级从高到低； 3、位运算符的运算功能： a、按位取反： ~01001101 = 101
14点睛Spring4.1-脚本编程 wiselyman spring4
14.1 Scripting脚本编程脚本语言和java这类静态的语言的主要区别是:脚本语言无需编译,源码直接可运行; 如果我们经常需要修改的某些代码,每一次我们至少要进行编译,打包,重新部署的操作,步骤相当麻烦; 如果我们的应用不允许重启,这在现实的情况中也是很常见的; 在spring中使用脚本编程给上述的应用场景提供了解决方案,即动态加载bean; spring支持脚本

按字母分类： A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 其他