蓝桥杯--2014第五届C/C++B组省赛
相比较2013年的省赛题,难度提高了,特别时对于搜索的考点
标题:啤酒和饮料
啤酒每罐2.3元,饮料每罐1.9元。小明买了若干啤酒和饮料,一共花了82.3元。
我们还知道他买的啤酒比饮料的数量少,请你计算他买了几罐啤酒。
注意:答案是一个整数。请通过浏览器提交答案。
不要书写任何多余的内容(例如:写了饮料的数量,添加说明文字等)。
解题思路:简单数学贪心题,枚举一下
答案:11
#include 标题:切面条
一根高筋拉面,中间切一刀,可以得到2根面条。
如果先对折1次,中间切一刀,可以得到3根面条。
如果连续对折2次,中间切一刀,可以得到5根面条。
那么,连续对折10次,中间切一刀,会得到多少面条呢?
答案是个整数,请通过浏览器提交答案。不要填写任何多余的内容。
解题思路:类似于左神的折纸问题,实际上都是一种树的算法,转化成搜索求解。假设每次折纸直接是按折痕切成两片,然后切一刀就是f(n) = f(n - 1) * 2。而实际上没有做上面那步操作时,摊开的纸条一定有一张是连着的,也就是数量要- 1。所以搜索式:f(n) = f(n - 1) * 2 - 1。利用数组打表求得f[10]。这题也可以直接找规律,注意要多考虑f[3]的值,否则容易直接写成斐波那契数列。
答案:1025
#include 标题:李白打酒
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒2斗。他边走边唱:
无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店5次,遇到花10次,已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白遇到店和花的次序,可以把遇店记为a,遇花记为b。则:babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢?请你计算出所有可能方案的个数(包含题目给出的)。
注意:通过浏览器提交答案。答案是个整数。不要书写任何多余的内容。
解题思路:搜索模拟一下,注意可能喝完酒了,但不足把所有遇花或遇店的情况加进来,要check掉。
答案:14
#include 标题:史丰收速算
史丰收速算法的革命性贡献是:从高位算起,预测进位。不需要九九表,彻底颠覆了传统手算!
速算的核心基础是:1位数乘以多位数的乘法。
其中,乘以7是最复杂的,就以它为例。
因为,1/7 是个循环小数:0.142857...,如果多位数超过 142857...,就要进1
同理,2/7, 3/7, ... 6/7 也都是类似的循环小数,多位数超过 n/7,就要进n
下面的程序模拟了史丰收速算法中乘以7的运算过程。
乘以 7 的个位规律是:偶数乘以2,奇数乘以2再加5,都只取个位。
乘以 7 的进位规律是:
满 142857... 进1,
满 285714... 进2,
满 428571... 进3,
满 571428... 进4,
满 714285... 进5,
满 857142... 进6
请分析程序流程,填写划线部分缺少的代码。
//计算个位
int ge_wei(int a)
{
if(a % 2 == 0)
return (a * 2) % 10;
else
return (a * 2 + 5) % 10;
}
//计算进位
int jin_wei(char* p)
{
char* level[] = {
"142857",
"285714",
"428571",
"571428",
"714285",
"857142"
};
char buf[7];
buf[6] = '\0';
strncpy(buf,p,6);
int i;
for(i=5; i>=0; i--){
int r = strcmp(level[i], buf);
if(r<0) return i+1;
while(r==0){
p += 6;
strncpy(buf,p,6);
r = strcmp(level[i], buf);
if(r<0) return i+1;
______________________________; //填空
}
}
return 0;
}
//多位数乘以7
void f(char* s)
{
int head = jin_wei(s);
if(head > 0) printf("%d", head);
char* p = s;
while(*p){
int a = (*p-'0');
int x = (ge_wei(a) + jin_wei(p+1)) % 10;
printf("%d",x);
p++;
}
printf("\n");
}
int main()
{
f("428571428571");
f("34553834937543");
return 0;
}
注意:通过浏览器提交答案。只填写缺少的内容,不要填写任何多余的内容(例如:说明性文字)
解题思路:读懂代码,发现程序到达横线处实际上r必定>=0。如果等于0说明还要往后考虑是否还有进位让这个数大于目标数。否则就是有进位也不足以让它大于,直接return i。
答案:if (r > 0) return i
#include 标题:打印图形
小明在X星球的城堡中发现了如下图形和文字:
rank=3
*
* *
* *
* * * *
rank=5
*
* *
* *
* * * *
* *
* * * *
* * * *
* * * * * * * *
* *
* * * *
* * * *
* * * * * * * *
* * * *
* * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
ran=6
*
* *
* *
* * * *
* *
* * * *
* * * *
* * * * * * * *
* *
* * * *
* * * *
* * * * * * * *
* * * *
* * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
* *
* * * *
* * * *
* * * * * * * *
* * * *
* * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
* * * *
* * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
小明开动脑筋,编写了如下的程序,实现该图形的打印。
#define N 70
void f(char a[][N], int rank, int row, int col)
{
if(rank==1){
a[row][col] = '*';
return;
}
int w = 1;
int i;
for(i=0; i解题思路:这个不会,同过debug一步步观察递归变化值去测试吧
答案:f(a, rank-1, row, col+w/2)
#include 标题:奇怪的分式
上小学的时候,小明经常自己发明新算法。一次,老师出的题目是:
1/4 乘以 8/5
小明居然把分子拼接在一起,分母拼接在一起,答案是:18/45 (参见图1.png)
老师刚想批评他,转念一想,这个答案凑巧也对啊,真是见鬼!
对于分子、分母都是 1~9 中的一位数的情况,还有哪些算式可以这样计算呢?
请写出所有不同算式的个数(包括题中举例的)。
显然,交换分子分母后,例如:4/1 乘以 5/8 是满足要求的,这算做不同的算式。
但对于分子分母相同的情况,2/2 乘以 3/3 这样的类型太多了,不在计数之列!
注意:答案是个整数(考虑对称性,肯定是偶数)。请通过浏览器提交。不要书写多余的内容。
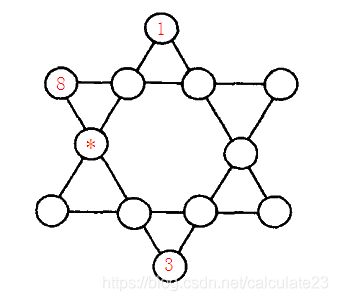
#include 标题:六角填数
如图【1.png】所示六角形中,填入1~12的数字。
使得每条直线上的数字之和都相同。
图中,已经替你填好了3个数字,请你计算星号位置所代表的数字是多少?
请通过浏览器提交答案,不要填写多余的内容。
#include 标题:蚂蚁感冒
长100厘米的细长直杆子上有n只蚂蚁。它们的头有的朝左,有的朝右。
每只蚂蚁都只能沿着杆子向前爬,速度是1厘米/秒。
当两只蚂蚁碰面时,它们会同时掉头往相反的方向爬行。
这些蚂蚁中,有1只蚂蚁感冒了。并且在和其它蚂蚁碰面时,会把感冒传染给碰到的蚂蚁。
请你计算,当所有蚂蚁都爬离杆子时,有多少只蚂蚁患上了感冒。
【数据格式】
第一行输入一个整数n (1 < n < 50), 表示蚂蚁的总数。
接着的一行是n个用空格分开的整数 Xi (-100 < Xi < 100), Xi的绝对值,表示蚂蚁离开杆子左边端点的距离。正值表示头朝右,负值表示头朝左,数据中不会出现0值,也不会出现两只蚂蚁占用同一位置。其中,第一个数据代表的蚂蚁感冒了。
要求输出1个整数,表示最后感冒蚂蚁的数目。
例如,输入:
3
5 -2 8
程序应输出:
1
再例如,输入:
5
-10 8 -20 12 25
程序应输出:
3
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include , 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
解题思路:由于蚂蚁没区别,两个蚂蚁碰头时实际上就是互相让道一下走过去,于是就是看第一只感冒的蚂蚁左边方向朝右的以及右边方向朝左的。
#include 标题:地宫取宝
X 国王有一个地宫宝库。是 n x m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。
地宫的入口在左上角,出口在右下角。
小明被带到地宫的入口,国王要求他只能向右或向下行走。
走过某个格子时,如果那个格子中的宝贝价值比小明手中任意宝贝价值都大,小明就可以拿起它(当然,也可以不拿)。
当小明走到出口时,如果他手中的宝贝恰好是k件,则这些宝贝就可以送给小明。
请你帮小明算一算,在给定的局面下,他有多少种不同的行动方案能获得这k件宝贝。
【数据格式】
输入一行3个整数,用空格分开:n m k (1<=n,m<=50, 1<=k<=12)
接下来有 n 行数据,每行有 m 个整数 Ci (0<=Ci<=12)代表这个格子上的宝物的价值
要求输出一个整数,表示正好取k个宝贝的行动方案数。该数字可能很大,输出它对 1000000007 取模的结果。
例如,输入:
2 2 2
1 2
2 1
程序应该输出:
2
再例如,输入:
2 3 2
1 2 3
2 1 5
程序应该输出:
14
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include , 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
解题思路:搜索+记忆化,不好写,现场比赛的话可能也只能写出个搜索
#include
标题:小朋友排队
n 个小朋友站成一排。现在要把他们按身高从低到高的顺序排列,但是每次只能交换位置相邻的两个小朋友。
每个小朋友都有一个不高兴的程度。开始的时候,所有小朋友的不高兴程度都是0。
如果某个小朋友第一次被要求交换,则他的不高兴程度增加1,如果第二次要求他交换,则他的不高兴程度增加2(即不高兴程度为3),依次类推。当要求某个小朋友第k次交换时,他的不高兴程度增加k。
请问,要让所有小朋友按从低到高排队,他们的不高兴程度之和最小是多少。
如果有两个小朋友身高一样,则他们谁站在谁前面是没有关系的。
【数据格式】
输入的第一行包含一个整数n,表示小朋友的个数。
第二行包含 n 个整数 H1 H2 … Hn,分别表示每个小朋友的身高。
输出一行,包含一个整数,表示小朋友的不高兴程度和的最小值。
例如,输入:
3
3 2 1
程序应该输出:
9
【样例说明】
首先交换身高为3和2的小朋友,再交换身高为3和1的小朋友,再交换身高为2和1的小朋友,每个小朋友的不高兴程度都是3,总和为9。
【数据规模与约定】
对于10%的数据, 1<=n<=10;
对于30%的数据, 1<=n<=1000;
对于50%的数据, 1<=n<=10000;
对于100%的数据,1<=n<=100000,0<=Hi<=1000000。
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include , 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
解题思路:每个位置逆序数之和,注意每个数是一个等差数列前n项和。
代码:小朋友排队