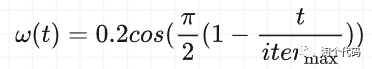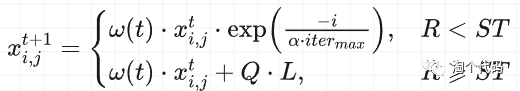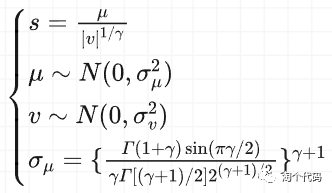自适应螺旋飞行麻雀搜索算法(ASFSSA),MATLAB代码免费获取
本期为大家带来的是由Ouyang C等人基于麻雀搜索算法提出一种自适应螺旋飞行麻雀搜索算法(Adaptive Spiral Flying Sparrow Search Algorithm,ASFSSA)。该算法提出四种改进策略,以提高算法的收敛精度和避免陷入局部最优。
参考文献:Ouyang C, Qiu Y, Zhu D. Adaptive spiral flying sparrow search algorithm[J]. Scientific Programming, 2021, 2021: 1-16.
关于原始麻雀算法的原理网上有很多,本文就不再详细介绍,下面直接讲解本文自适应螺旋飞行麻雀搜索算法改进的策略。
①混沌映射策略
论文中采用了tent混沌映射对麻雀算法的粒子进行初始化,有关混沌映射的之前文章已经讲过很多,这里就不再细讲,可以参考这篇文章:10种混沌映射优化灰狼算法,可一键切换,可用于优化所有群智能算法
②自适应加权策略
引入自适应权重能够提高发现者个体位置的质量,使其他个体能够更快地收敛到最优位置,并加快收敛速度,自适应权重的公式如下:
改进发现者位置更新的公式如下:
通过引入自适应权重进行动态调整麻雀的位置,通过不同的引导模式不同时间的发现者,提高算法的搜索灵活。随着迭代次数的增加,麻雀个体向最佳位置会聚,权重越大个体移动越快,因此提高了算法的收敛速度。
③莱维飞行策略
在使用发现者位置更新完之后,采用莱维飞行策略,对发现者的位置再次更新,莱维飞行机制和自适应权重的结合平衡了搜索方法,并且使所获得的每个解的质量都得到了一定的提高,因此很大程度上增强算法的搜索能力。莱维飞行公式如下:
④可变螺旋搜索策略
螺旋搜索是参考鲸鱼算法,在普通螺旋搜索的基础上,通过改变螺旋搜索因子,使其动态变化,可以提升算法的搜索效率。在追随者位置更新阶段,引入可变螺旋位置更新策略,使追随者位置更新变得更加灵活,并平衡了算法的全局搜索和局部搜索。可变螺旋位置更新策略的公式如下:
式中, 参数随操作次数而变化,螺旋线的大小和振幅根据 函数的财产进行动态调整。 表示变化系数, ; 表示一个均匀分布随机数, 。
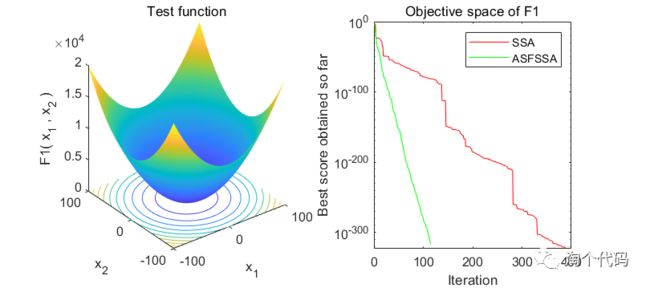
自适应螺旋飞行麻雀搜索算法在CEC2005测试结果如下:
将原始麻雀算法和改进麻雀算法分别迭代500次,麻雀个数设置为30个,每个函数运行30次,求最优值,最差值,平均值,方差,中值共五个指标如下:
F1函数计算结果:
SSA:最优值:4.3074e-272 最差值:3.435e-70 平均值:1.2104e-71 方差:6.2663e-71 中值:1.8503e-90
ASFSSA:最优值:0 最差值:0 平均值:0 方差:0 中值:0
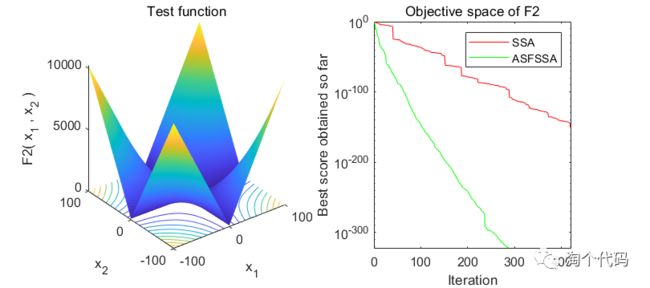
F2函数计算结果:
SSA:最优值:3.0364e-66 最差值:3.3144e-36 平均值:1.2236e-37 方差:6.0434e-37 中值:7.4176e-44
ASFSSA:最优值:4.6839e-193 最差值:4.9652e-178 平均值:1.6595e-179 方差:0 中值:7.3611e-187
F3函数计算结果:
SSA:最优值:0 最差值:3.5193e-34 平均值:1.4068e-35 方差:6.508e-35 中值:1.2581e-44
ASFSSA:最优值:0 最差值:0 平均值:0 方差:0 中值:0
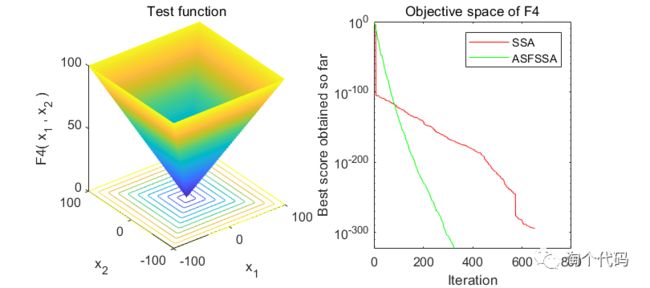
F4函数计算结果:
SSA:最优值:8.1653e-177 最差值:9.6852e-30 平均值:5.3915e-31 方差:1.838e-30 中值:1.892e-41
ASFSSA:最优值:6.776e-301 最差值:5.8606e-167 平均值:1.9535e-168 方差:0 中值:1.1965e-178
F5函数计算结果:
SSA:最优值:5.7208e-11 最差值:0.00028058 平均值:1.5325e-05 方差:5.3195e-05 中值:3.232e-07
ASFSSA:最优值:1.855e-08 最差值:0.10666 平均值:0.0039251 方差:0.019419 中值:3.118e-05
F6函数计算结果:
SSA:最优值:0 最差值:7.7037e-32 平均值:9.3472e-33 方差:1.5365e-32 中值:3.0815e-33
ASFSSA:最优值:0 最差值:4.9304e-32 平均值:8.6282e-33 方差:1.2337e-32 中值:3.0815e-33
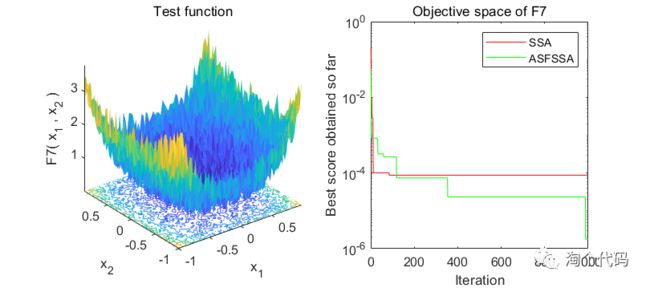
F7函数计算结果:
SSA:最优值:0.00011095 最差值:0.0049268 平均值:0.0011296 方差:0.0010227 中值:0.00089266
ASFSSA:最优值:1.0841e-06 最差值:0.0018575 平均值:0.00032377 方差:0.0004119 中值:0.00016401
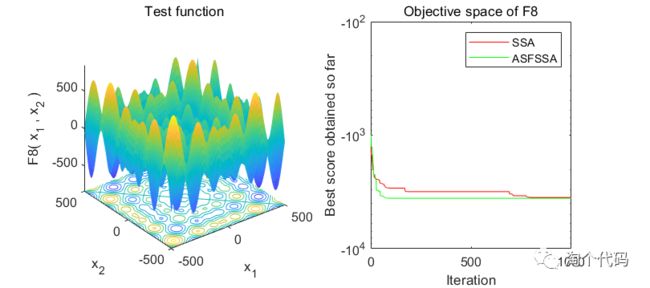
F8函数计算结果:
SSA:最优值:-3952.9522 最差值:-2668.2847 平均值:-3262.8123 方差:327.1847 中值:-3261.2452
ASFSSA:最优值:-4189.8289 最差值:-3117.8156 平均值:-3603.3574 方差:302.5694 中值:-3684.9435
F9函数计算结果:
SSA:最优值:0 最差值:0 平均值:0 方差:0 中值:0
ASFSSA:最优值:0 最差值:0 平均值:0 方差:0 中值:0
F10函数计算结果:
SSA:最优值:4.4409e-16 最差值:4.4409e-16 平均值:4.4409e-16 方差:0 中值:4.4409e-16
ASFSSA:最优值:4.4409e-16 最差值:4.4409e-16 平均值:4.4409e-16 方差:0 中值:4.4409e-16
F11函数计算结果:
SSA:最优值:0 最差值:0 平均值:0 方差:0 中值:0
ASFSSA:最优值:0 最差值:0 平均值:0 方差:0 中值:0
F12函数计算结果:
SSA:最优值:4.7116e-32 最差值:4.9052e-32 平均值:4.7738e-32 方差:6.3457e-34 中值:4.7721e-32
ASFSSA:最优值:4.7116e-32 最差值:6.2606e-32 平均值:4.9674e-32 方差:3.8449e-33 中值:4.8205e-32
F13函数计算结果:
SSA:最优值:1.3498e-32 最差值:3.3219e-32 平均值:1.7196e-32 方差:5.6252e-33 中值:1.3498e-32
ASFSSA:最优值:1.3498e-32 最差值:1.1619e-29 平均值:4.0982e-31 方差:2.1174e-30 中值:1.473e-32
F14函数计算结果:
SSA:最优值:0.998 最差值:12.6705 平均值:6.3206 方差:5.6898 中值:1.9901
ASFSSA:最优值:0.998 最差值:12.6705 平均值:5.6798 方差:5.228 中值:2.9821
F15函数计算结果:
SSA:最优值:0.00030749 最差值:0.00057747 平均值:0.00032635 方差:6.2713e-05 中值:0.00030749
ASFSSA:最优值:0.00030749 最差值:0.0012232 平均值:0.00071963 方差:0.00042443 中值:0.00047542
F16函数计算结果:
SSA:最优值:-1.0316 最差值:-1.0316 平均值:-1.0316 方差:5.6082e-16 中值:-1.0316
ASFSSA:最优值:-1.0316 最差值:-1.0316 平均值:-1.0316 方差:4.7373e-16 中值:-1.0316
F17函数计算结果:
SSA:最优值:0.39789 最差值:0.39789 平均值:0.39789 方差:0 中值:0.39789
ASFSSA:最优值:0.39789 最差值:0.39789 平均值:0.39789 方差:0 中值:0.39789
F18函数计算结果:
SSA:最优值:3 最差值:30 平均值:3.9 方差:4.9295 中值:3
ASFSSA:最优值:3 最差值:3 平均值:3 方差:1.9305e-15 中值:3
F19函数计算结果:
SSA:最优值:-3.8628 最差值:-3.0898 平均值:-3.837 方差:0.14113 中值:-3.8628
ASFSSA:最优值:-3.8628 最差值:-3.8628 平均值:-3.8628 方差:2.2599e-15 中值:-3.8628
F20函数计算结果:
SSA:最优值:-3.322 最差值:-3.2031 平均值:-3.2863 方差:0.055415 中值:-3.322
ASFSSA:最优值:-3.322 最差值:-3.2031 平均值:-3.2779 方差:0.057935 中值:-3.322
F21函数计算结果:
SSA:最优值:-10.1532 最差值:-5.0552 平均值:-8.2839 方差:2.4987 中值:-10.1532
ASFSSA:最优值:-10.1532 最差值:-5.0552 平均值:-7.0604 方差:2.3849 中值:-5.0552
F22函数计算结果:
SSA:最优值:-10.4029 最差值:-5.0877 平均值:-9.3388 方差:2.1619 中值:-10.4029
ASFSSA:最优值:-10.4029 最差值:-5.0877 平均值:-6.8024 方差:2.4436 中值:-5.0877
F23函数计算结果:
SSA:最优值:-10.5364 最差值:-5.1285 平均值:-8.914 方差:2.5206 中值:-10.5364
ASFSSA:最优值:-10.5364 最差值:-5.1285 平均值:-6.163 方差:2.1086 中值:-5.1285代码展示
代码严格根据原始论文复现,完整代码如下,大家直接复制粘贴即可。(注意,需要配合CEC函数使用哦,关于CEC函数的调用往期文章已经讲过很多啦,这里就不再细说)
%代码严格根据论文复现
function [fMin , bestX,Convergence_curve ] = ASFSSA(pop, M,c,d,dim,fobj )
P_percent = 0.2; % The population size of producers accounts for "P_percent" percent of the total population size
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
pNum = round( pop * P_percent ); % The population size of the producers
lb= c.*ones( 1,dim ); % Lower limit/bounds/ a vector
ub= d.*ones( 1,dim ); % Upper limit/bounds/ a vector
%Initialization
N = pop*dim;
z(1)=rand;
for k=1:N
z(k+1) = mod(2 * z(k)+rand * (1/N),1);
end
for i = 1 : pop
for j=1:dim
G(i,j) = z((i-1)*dim+j+1);
x(i,j) = lb(j) + (ub(j) - lb(j)) * G(i,j);
end
fit( i ) = fobj( x( i, : ) ) ;
end
pFit = fit;
pX = x; % The individual's best position corresponding to the pFit
[ fMin, bestI ] = min( fit ); % fMin denotes the global optimum fitness value
bestX = x( bestI, : ); % bestX denotes the global optimum position corresponding to fMin
% Start updating the solutions.
for t = 1 : M
[ ans, sortIndex ] = sort( pFit );% Sort.
[fmax,B]=max( pFit );
worse= x(B,:);
r2=rand(1);
w = 0.2 * cos(pi/2 * (1-(t/M)));
if(r2<0.8)
for i = 1 : pNum % Equation (3)
r1=rand(1);
x( sortIndex( i ), : ) = w * pX( sortIndex( i ), : )*exp(-(i)/(r1*M));
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );
end
else
for i = 1 : pNum
x( sortIndex( i ), : ) = w * pX( sortIndex( i ), : )+randn(1)*ones(1,dim);
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );
end
end
[ ~, bestII ] = min( fit );
bestXX = x( bestII, : );
for i = 1 : pNum
x(sortIndex( i ), : ) = func_levy( x( sortIndex( i ), : ),bestXX );
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );
end
[ ~, bestII ] = min( fit );
bestXX = x( bestII, : );
for i = ( pNum + 1 ) : pop % Equation (4)
k=5;
A=floor(rand(1,dim)*2)*2-1;
sz =[1,dim];
L = unifrnd(-1,1,sz);
xb(i,:) = bestXX+(abs(( pX( sortIndex( i ), : )-bestXX)))*(A'*(A*A')^(-1))* L;
z = exp(k*cos(pi*(1-(t/M))));
if( i>(pop/2))
for j = 1:dim
l = 0.01 .*( x( sortIndex(i),j) - bestXX(j));
x( sortIndex(i) , j )=exp(z*l) * cos(2*pi*l) * randn(1)*exp((worse(j)-pX( sortIndex( i ), j ))/(i)^2);
end
else
for j = 1:dim
l = 0.01 .*( x( sortIndex(i),j) - bestXX(j));
x( sortIndex(i) , j ) = xb(i,j) * exp(z*l) * cos(2*pi*l);
end
end
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );
end
c=randperm(numel(sortIndex));
b=sortIndex(c(1:20));
for j = 1 : length(b) % Equation (5)
if( pFit( sortIndex( b(j) ) )>(fMin) )
x( sortIndex( b(j) ), : )=bestX+(randn(1,dim)).*(abs(( pX( sortIndex( b(j) ), : ) -bestX)));
else
x( sortIndex( b(j) ), : ) =pX( sortIndex( b(j) ), : )+(2*rand(1)-1)*(abs(pX( sortIndex( b(j) ), : )-worse))/ ( pFit( sortIndex( b(j) ) )-fmax+1e-50);
end
x( sortIndex(b(j) ), : ) = Bounds( x( sortIndex(b(j) ), : ), lb, ub );
fit( sortIndex( b(j) ) ) = fobj( x( sortIndex( b(j) ), : ) );
end
for i = 1 : pop
if ( fit( i ) < pFit( i ) )
pFit( i ) = fit( i );
pX( i, : ) = x( i, : );
end
if( pFit( i ) < fMin )
fMin= pFit( i );
bestX = pX( i, : );
end
end
Convergence_curve(t)=fMin;
end
% Application of simple limits/bounds
function s = Bounds( s, Lb, Ub)
% Apply the lower bound vector
temp = s;
I = temp < Lb;
temp(I) = Lb(I);
% Apply the upper bound vector
J = temp > Ub;
temp(J) = Ub(J);
% Update this new move
s = temp;完整代码链接:
链接:https://pan.baidu.com/s/1gRHRJijsdl12eV9XM4qpxQ?pwd=g7h9
提取码:g7h9