数据结构-二叉排序树(BST树)
目录
1,二叉排序树介绍
1.1,二叉排序树的构建和插入
1.2,二叉排序树的查找过程
1.3,二叉排序树的性能分析
2,二叉排序树的实现
2.1,二叉排序树的节点类型
2.2,二叉排序树的查找操作
2.3,递归构建二叉排序树
2.4,中序遍历二叉树
2.5,二叉排序树的删除操作
2.5.1,查找待删除的节点
2.5.2,查找待删除节点的父节点
2.6.查找最大值和最小值
2.7,创建一颗二叉排序树
2.8,测试代码
2.9,二叉排序树小结
1,二叉排序树介绍
二叉排序树(Binary Sort Tree)或者是一颗空树;或者是具有如下性质的二叉树:
- 若它的左子树不空,则 左子树 上所有结点的值 均小于 它的根结点的值;
- 若它的右子树不空,则 右子树 上所有结点的值 均大于 它的根结点的值;
- 它的 左、右子树又分别为二叉排序树 。
显然二叉排序树的定义是一个递归形式的定义,所以后面景禹要讲的插入、查找和删除都是基于递归的形式。特别说明:如果有相同的值,可以将该节点放在左子节点或右子节点
1.1,二叉排序树的构建和插入
- 假设我们有初始的无序序列:
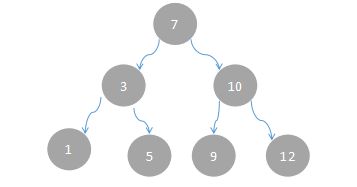
- 第一步:插入7作为我们二叉排序树的根节点。
- 第二步:插入节点3,3和7进行比较,发现3小于根节点7,那么就把3这个节点作为7的左子树。
- 第三步:插入节点10,发现节点10比根节点的值7大,于是就把10这个节点作为根节点的左子节点插入其右边。
- 第四步:插入节点12,发现12比根节点7大,于是就再和节点7的右子节点比较,但是10小于节点12,所以就把节点12作为10这个节点的右孩子节点。
- 第五步:插入节点5,5小于根节点7,于是就把5和根节点的左孩子3比较,5大于3,所以节点5作为节点3的右孩子节点。
- 第六步:插入节点1,1和7比较,小于7,然后再和3比较,小于3,于是就作为节点3的左孩子。
- 第七步:插入节点9,9大于根节点7,但是小于节点10,于是就把9作为节点10的左孩子。
经过多次的插入节点,最终我们建立的二叉排序树如上图所示。我们对建立好的二叉排序树做中序遍历操作,发现遍历结果是一个有序的序列,这也是二叉排序树的特点:中序遍历有序。
1.2,二叉排序树的查找过程
二叉查找树的查找是从根节点开始的,延某一个分支逐渐向下比较的过程,如果二叉树非空,那么就把给定的值先和根节点进行比较,如果相等,那么就查找成功,如果小于根节点,那么就在根节点的左子树上面进行递归查找,如果大于根节点的值,就在根节点的右子树上面进行递归查找。
1.3,二叉排序树的性能分析
二叉排序树的查找性能主要取决于树的高度,如果二叉排序树的左右子树的高度差不超过1,那么这样的树称为平衡二叉树,后面会介绍,这样的平衡二叉树的平均查找长度是![]() ,但是如果二叉排序树构建的是一棵单支树,那么查找效率最差,和线性查找几乎差不多,为
,但是如果二叉排序树构建的是一棵单支树,那么查找效率最差,和线性查找几乎差不多,为![]() ,所以我们在构建二叉排序树的时候力求构建的二叉排序树尽可能的低,最好的二叉排序树是二分查找生成的二叉判定树。当然,对于二叉排序树可能生成单支树的情况,后面我们还有更好的解决办法----AVL树。
,所以我们在构建二叉排序树的时候力求构建的二叉排序树尽可能的低,最好的二叉排序树是二分查找生成的二叉判定树。当然,对于二叉排序树可能生成单支树的情况,后面我们还有更好的解决办法----AVL树。
2,二叉排序树的实现
2.1,二叉排序树的节点类型
//二叉排序树的节点类型
class BSTNode{
private int data;
BSTNode left;
BSTNode right;
public BSTNode(int data) {
this.data = data;
}
public int getData() {
return data;
}
public BSTNode getLeft() {
return left;
}
public BSTNode getRight() {
return right;
}
public void setData(int data) {
this.data = data;
}
public void setLeft(BSTNode left) {
this.left = left;
}
public void setRight(BSTNode right) {
this.right = right;
}
@Override
public String toString() {
return "BSTNode{" +
"data=" + data +
'}';
}
}2.2,二叉排序树的查找操作
二分查找是在一个有序数组上进行的,就像前面我们通过对二叉排序树进行中序遍历得到的结果一样,初始时,我们将整个有序数组当做二分查找的搜索空间,然后计算搜索空间的中间元素,并与查找元素进行比较;然后将整个搜索空间缩减一半;重复上面的步骤,直到找到待查找元素或者返回查找失败的信息。二叉排序树的查找操作和二分查找类似,每一次都和子树的根节点进行比较,直到查找到为止。
/**
* 二叉排序树中查找一个元素,根据节点的值进行查找
* @param value 待查找节点的值
* @return 查找到就返回该节点,否则返回null
*/
public BSTNode searchValue(int value){
if(this.getData() == value){
return this;
}else if(value this.getData()){
if(this.right == null){
return null;
}
return this.right.searchValue(value);
}
return null;
} 2.3,递归构建二叉排序树
从上面二叉排序树的查找过程可以看出,查找是一个递归的过程,而建立二叉排序树也是一个递归的过程。对于任意一个待插入的元素 x 都是插入在二叉排序树的叶子结点,问题的关键就是确定插入的位置,原理当然和上面的查找操作一样,从根结点开始进行判断,直到到达叶子结点,则将待插入的元素作为一个叶子结点插入即可。
/**
* 向二叉排序树中添加一个节点
* @param node 需要添加的节点
*/
public void add(BSTNode node){
// 判断添加的节点是否是空
if(node == null){
return ;
}
// 判断当前节点的值和根节点的值大小
if(node.getData() < this.getData()){
if(this.getLeft() == null){
// 如果左子节点为空,直接挂上去即可
this.left=node;
}else {
// 如果不是空,就递归进行向左子树添加
this.left.add(node);
}
}else {
// 判断左子树是否是空,空的话直接添加节点
if(this.right == null){
this.right=node;
}else {
// 不空的话递归在左子树进行添加
this.right.add(node);
}
}
}2.4,中序遍历二叉树
// 中序遍历二叉树
public void midOrder(){
if(this == null){
return;
}
if(this.left != null){
this.left.midOrder();
}
System.out.println(this.getData());
if(this.right != null){
this.right.midOrder();
}
}2.5,二叉排序树的删除操作
二叉排序树的删除一个节点稍稍麻烦,因为我们每删除一个节点的时候,需要保证删除后仍然符合二叉排序树的定义,二叉排序树的删除操作分为三种情况,下面我们来看具体是如何删除一个节点。
- 假如我们删除的是一个叶子结点:如果删除的是二叉排序树的一个叶子节点,那我们查找到这个节点之后就可以直接删除,因为删除叶子结点不会影响我们二叉排序树的整体情况,仍然是一棵二叉排序树,符合二叉排序树的定义。对于上面建立好的二叉树,如果我们删除叶子结点12,那么二叉排序树删除后的形态如下:
- 被删除的结点D仅有一个孩子:如果只有左孩子,没有右孩子,那么只需要把要删除结点的左孩子链接到要删除结点的父亲节点,然后删除D结点就好了;如果只有右孩子,没有左孩子,那么只要将要删除结点D的右孩子重接到要删除结点D的父亲结点。我们以删除节点10为例:
对于要删除的节点10,只有一个左子节点,那我们把节点10删除后,需要用他的左子节点来代补充他的位置。
- 被删除结点的左右孩子都存在:对于这种情况,我们有两种处理方法。下面我们以删除节点3为例。
- 第一步:我们先获取待删除节点右子树上的最小值,在这里也可以获取待删除节点左子树上的最小值。
- 第二步:我们已经找到待删除节点右子树上的最小值,这一步我们使用这个最小值代替待删除节点里面的值,然后把这个最小值节点删除即可。
- 补充:我们也可以找到待删除节点左子树上的最大值,做同样的处理即可。
2.5.1,查找待删除的节点
/**
* 查找要删除的节点
* @param value 要查找节点的值
* @return 如果找到该节点就返回,否则就返回null
*/
public BSTNode search(int value){
if(this.getData() == value){
return this;
}else if(value < this.getData()){
if(this.left == null){
return null;
}
// 左子树递归查找
return this.left.search(value);
}else {
if(this.right == null){
return null;
}
return this.right.search(value);
}
}2.5.2,查找待删除节点的父节点
/**
* 查找要删除节点的父节点
* @param value 要删除节点的值
* @return 查找到就返回
*/
public BSTNode searchParent(int value){
if((this.left != null && this.left.getData()==value)||(this.right != null && this.right.getData()==value)){
return this;
}else {
// 如果待查找的节点值小于当前的节点的值,并且当前节点的左子树不是空,就递归在左子树查找
if( value < this.getData()&& this.left != null){
return this.left.searchParent(value);
}else if(value >=this.getData()&& this.right != null){
return this.right.searchParent(value);
}else {
// 没有找到父节点
return null;
}
}
}2.6.查找最大值和最小值
/**
* 查找二叉排序树中的最小值
* @return 返回最小值的节点
*/
public BSTNode searchMinBSTNode(){
BSTNode bstNode=this;
if(bstNode!= null){
while (bstNode.getLeft()!= null){
bstNode=bstNode.getLeft();
}
return bstNode;
}else {
return null;
}
}
/**
* 查找二叉排序树中的最大值
* @return
*/
public BSTNode searchMaxBSTNode(){
BSTNode bstNode=this;
if(bstNode!= null){
while (bstNode.getRight()!= null){
bstNode=bstNode.getRight();
}
return bstNode;
}else {
return null;
}
}2.7,创建一颗二叉排序树
//创建一棵二叉排序树
class BinarySortedTree{
private BSTNode root;
/**
* 查找二叉排序树中的最小值节点
* @return 返回最大值的节点
*/
public BSTNode searchMinBSTNode(){
if(this.root == null){
return null;
}else {
return this.root.searchMinBSTNode();
}
}
/**
* 查找二叉排序树中的最大值节点
* @return 返回最大值的节点
*/
public BSTNode searchMaxBSTNode(){
if(this.root == null){
return null;
}else {
return this.root.searchMaxBSTNode();
}
}
public BSTNode searchValue(int value){
if(this.root== null){
return null;
}else {
return this.root.searchValue(value);
}
}
/**
* 向二叉排序树中添加一个节点
* @param node 待添加而定节点
*/
public void add(BSTNode node){
if(this.root == null){
this.root=node;
}else {
this.root.add(node);
}
}
/**
* 中序遍历二叉树
*/
public void midOrder(){
if(this.root == null){
System.out.println("当前二叉排序树是空树!");
return;
}else {
this.root.midOrder();
}
}
/**
* 查找延删除的节点
* @param value 待查找节点的值
* @return 发挥查找到的节点
*/
public BSTNode Search(int value){
if(this.root == null)
return null;
else {
return this.root.search(value);
}
}
/**
* 查找待删除节点的父节点
* @param value 待删除节点的值
* @return 返回查找到的值
*/
public BSTNode searchParent(int value){
if(this.root ==null){
return null;
}else {
return this.root.searchParent(value);
}
}
/**
* 删除二叉排序树中的一个节点
* @param value 待删除节点的值
*/
public void deleteNode(int value){
if(this.root == null){
return;
}else {
// 获取待删除的节点
BSTNode targetNode=Search(value);
if(targetNode == null){
// 如果没有找到待删除的节点
return;
}
// 如果我们发现当前二叉树只有一个节点
if(root.getLeft() ==null&& root.getRight() == null){
root=null;
return;
}
// 查找父节点
BSTNode parent=searchParent(value);
// 判断待删除节点是否是叶子结点
if(targetNode.getLeft() == null && targetNode.getRight() == null){
if(parent.getLeft() != null && parent.left.getData() == value){
// 说明当前节点是父节点的左子节点
parent.left=null;
}else if(parent.right != null && parent.right.getData() == value){
// 说明当前节点是父节点的右子节点
parent.right=null;
}
}else if(targetNode.getLeft() != null && targetNode.getRight() != null){
// 也就是说待删除节点的左右子节点都不是空
// 在右子树上面找到最小值节点删除
int minRight=delRightNodeMin(targetNode.right);
targetNode.setData(minRight);
// 在这里也可以从左子树找最大值的节点
}else {
// 删除只有一颗子树的节点
if(parent !=null){
// 如果树只剩下根节点和左子节点,需要特殊判断,因为根节点没有父节点
if(targetNode.left != null)
{
// 也即是待删除节点的左子树不空
if(parent.left.getData() ==value){
// 待删除节点是parent的左子节点
parent.left=targetNode.left;
// 待删除节点是parent的左子节点并且待删除节点也有左子节点
}else {
// 待删除节点是parent节点的右子节点
parent.right=targetNode.left;
}
}else {
if(parent!=null){
// 也就是要删除的节点有右子节点
if(parent.left.getData() ==value){
parent.left=targetNode.right;
}else {
// 待删除节点是parent节点的右子节点
parent.right=targetNode.right;
}
}else {
root=targetNode.right;
}
}
}else {
root=targetNode.left;
}
}
}
}
/**
* 返回以node为根节点的右子树上面的最小值节点,并且删除最小值节点
* @param node 作为子树的根节点
* @return 返回以node为根节点的右子树上最小值节点的值
*/
public int delRightNodeMin(BSTNode node){
BSTNode bstNode= node;
// 循环找到左子树节点
while (bstNode.left != null){
bstNode=bstNode.left;
}
// 退出循环,bstNode指向最小值的节点
deleteNode(bstNode.getData());
return bstNode.getData();
}
}
2.8,测试代码
public class BinarySortedTreeDemo {
public static void main(String[] args) {
int []arr={7,3,10,12,5,1,9,2};
// c创建一棵二叉排序树
BinarySortedTree binarySortedTree=new BinarySortedTree();
for(int i=0;i2.9,二叉排序树小结
每个结点的Ci为该结点的层次数。最好的情况是二叉排序树的形态和折半查找的判定树相同,其平均查找长度和logn成正比(O(log2(n)))。最坏情况下,当先后插入的关键字有序时,构成的二叉排序树为一棵斜树,树的深度为n,其平均查找长度为(n + 1) / 2。也就是时间复杂度为O(n),等同于顺序查找。因此,如果希望对一个集合按二叉排序树查找,最好是把它构建成一棵平衡的二叉排序树(平衡二叉树)。
- 小结:
- 二叉排序树是以链接的方式存储,保持了链接存储结构在执行插入或删除操作时不用移动元素的优点。只要找到合适的插入和删除位置后,仅需要修改链接指针即可。插入删除的时间性能比较好。
- 对于二叉排序树的查找,走的是根结点到要查找结点的路径,其比较次数等于给定值的结点在二叉排序树的层次。
- 注意:如果在建立二叉排序树的时候输入的序列是有序的,那么建立的二叉排序树将是一棵斜的树,此时查找性能最差,等于线性查找。
参考资料:
[1] https://www.jianshu.com/p/c6cb2c1460d0