tensorflow入门笔记(八)神经元
#
#作者:韦访
#博客:https://blog.csdn.net/rookie_wei
#微信:1007895847
#添加微信的备注一下是CSDN的
#欢迎大家一起学习
#
1、概述
喝完奶茶继续干,通过前面的学习,对深度学习似乎有那么点感觉了,本来想继续往下学学一些应用的例子的,但是现在我想还是系统的先把一些深度学习的基本概念总结一下,以及先系统的学习一下tensorflow的编程基础,工欲善其事,必先利其器。这一节就先说说神经元吧。
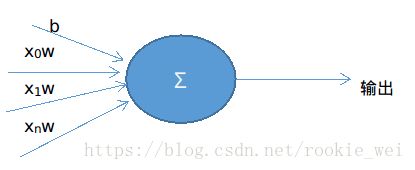
2、单个神经元
单个神经元网络模型如上图所示(画的有点丑),计算公式如下:
y = x0w+x1w+...+xnw+b=Ʃwi × xi + b = w • x + b
其中,y为输出结果,x为输入,w为权重,b为偏置。
训练神经网络,其实就是不断的调整w和b的值,使之得到一个合适的值,最终这个值配合运算公式形成的逻辑,就是神经网络的模型。
1、前向传播
不同的神经网络结构前向传播的方式是不一样的,最简单的前向传播算法就是上面的公式,输入x经过与权重w的加权和再加上偏置b,得到的结果y。
2、反向传播
网络训练前,我们当然不知道w和b的值是多少才是合适的值,反向传播的作用就是根据前向传播的到的结果与实际标签的误差,反馈给网络,网络根据误差来调整权重以得到更优值。
在实际应用中,一般都是经过多次迭代,一点一点修正w和b的值,直到模型的输出和实际标签的误差小于我们设定的某个阈值为止。
3、损失函数
损失函数就是我们上面说的用于描述模型输出结果和实际值的差距大小。
常用的损失函数有均方误差(MSE)和交叉熵。
5.1、均方误差
均方误差,也叫均值平方差,对于回归问题,一般最常用的损失函数就是均方误差。公式如下:
MSE = (Ʃj(yj - y`j)2) / n
其中,y表示真实值,y`表示预测值。
tensorflow实现均方误差的函数为:
mse = tf.reduce_mean(tf.square(y_ - y))
5.2、交叉熵
对于分类问题,一般最常用的损失函数是交叉熵。
假设两个概率分布p和q,通过q来表示p的交叉熵如下:
H(P) = - Ʃxp(x) log q(x)
tensorflow实现交叉熵的函数为:
cross_entropy = -tf.reduce_sum(labels * tf.log(logits))
或者
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(logits, labels)
5.3、分类问题和回归问题
既然上面说到分类问题和回归问题,这里就介绍一下这两类问题。
分类问题:分类问题希望解决的是将不同的样本分到事先定义好的类别中,比如判断一个零件是否合格的问题就是一个二分类问题。手写体数字识别问题是一个十分类问题(0~9十个数字)。
回归问题:回归问题解决的是对具体数值的预测。比如房价预测、销量预测等。这些问题所需要预测的不是一个事先定义好的类别,而是任意实数。解决回归问题一般只有一个输出节点,这个节点的输出值就是预测值。
6、优化器
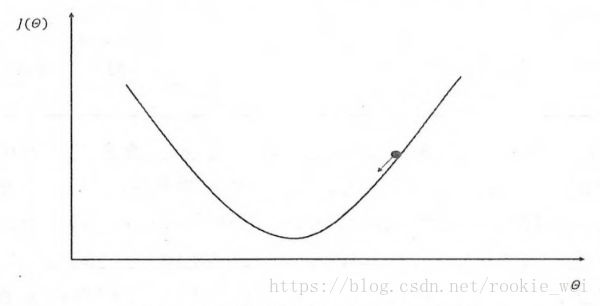
前面说过,反向传播是将预测值与实际值之间的误差,反馈给网络,网络再去优化权重,怎么优化权重,就是优化器函数该做的事了。常用的优化算法有梯度下降法。
如上图所示,假设θ表示神经网络的参数,J(θ)表示在给定的参数取值下,训练数据集上损失函数的大小,那么整个优化过程可以理解为寻找一个参数θ,使得J(θ)最小。梯度下降法会迭代式更新参数θ,不断沿着梯度的反方向让参数总是朝着总损失更小的方向更新。
tensorflow中,一般的梯度下降函数为:
tf.train.GradientDescentOptimizer
tf.train.AdadeltaOptimizer
tf.train.AdagradOptimizer
tf.train.MomentumOptimizer
tf.train.AdamOptimizer
tf.train.FtrlOptimizer
tf.train.RMSPropOptimizer
目前最常用的优化器是tf.train.AdamOptimizer函数。
在循环里面使用tf.train.AdamOptimizer函数接着minimize(loss)函数,优化器就会沿着loss最小值的方向优化参数了。比如:
train_step = tf.train.AdamOptimizer(learning_rate).minimize(loss)
7、学习率
每个优化器都会有一个学习率的参数,设置学习率的大小,是在精度和速度之间找到一个平衡,学习率决定了每次更新的速度,如果幅度过大,可能导致参数在极忧值两侧来回移动,如果幅度过小,就会大大降低优化速度。为了解决这个问题,tensorflow提供了一种更加灵活的学习率设置方法----指数衰减法。
tensorflow提供了tf.train.exponential_decay(learning_rate,global_step, decay_steps, decay_rate,staircase=False, name=None)
函数来设置指数衰减学习率,learning_rate代表初始学习率,如果staircase=True,则表示没有衰减功能。
8、激活函数
线性模型的局限性:只通过线性变换,任意层的全连接神经网络和单层神经网络的表达能力并没有任何区别,线性模型能解决的问题是有限的。
激活函数的目的是去线性化,如果将每一个神经元的输出通过一个非线性函数,那么整个神经网络的模型也就不再是线性的了,这个非线性函数就是激活函数。
8.1、ReLU函数
ReLU函数是个非常常用的激活函数,其公式为:
f(x) = max(0, x)
即,大于0的为其本身,否则为0.
tensorflow中,该激活函数为,
tf.nn.relu()
8.2 Sigmoid函数
其公式为:
y = 1 / (1 + e-x)
其中,x的范围为正无穷大到负无穷大,y的范围为0到1.
如上图所示,经过Sigmoid函数输出的函数都会在0~1区间里,但,可以看出,当x=10和x=1000其实输出的y差距并不大,所以可以看出,Sigmoid函数极限在x为-6到6之间,其中x在-3到3之间效果比较好。
tensorflow中,该激活函数为
tf.nn.sigmoid()
8.3 Tanh函数
其公式为:
y = (1 - e-2x) / (1 + e-2x)
其中,x的范围为正无穷大到负无穷大,y的范围为-1到1.
tensorflow中,该激活函数为
tf.nn.tanh()
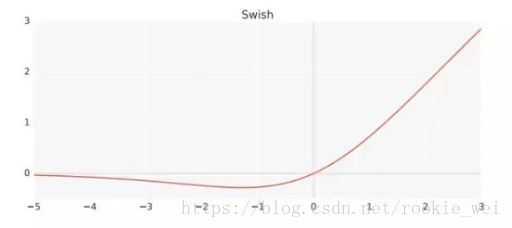
8.4 Swish函数
Swish激活函数的效果优于ReLU函数,公式如下:
y = x * sigmoid(βx)
其中,β为x的缩放参数,一般取1即可。
Tensorflow好像还没有定义该函数,但是我们可以用sigmoid函数自己定义,
def swish(x, b = 1):
return x * tf.nn.sigmoid(b * x)
9、Softmax函数
Softmax函数主要用来处理分类问题,该函数将前向传播结果转为概率问题,所有概率之和为1。例如对(a, b, c)用softmax函数后为,
(ea/(ea+eb+ec), eb/(ea+eb+ec), ec/(ea+eb+ec)).
在实际使用中,softmax函数的分类,一般都将分类标签转成one-hot编码,需要分成几类,就在这层放几个节点。例如前面说的MNIST数据集和CIFAR10数据集,最后一层的输出都是10个节点,因为这两个数据集都是十分类问题。
Tensorflow中,softmax函数为
tf.nn.softmax()
10、过拟合问题
所谓过拟合,指的是当一个模型过为复杂之后,它可以很好的记忆每一个训练数据中随机噪音的部分而忘了要去学习训练数据中的趋势。过度拟合训练数据中的随机噪音虽然可以得到非常小的损失函数,但是对于未知数据可能无法做出可靠的判断。如下图所示:
10.1 正则化
为了避免过拟合问题,一个非常常用的方法是正则化(regularization)。
正则化的思想是在损失函数中加入刻画模型复杂程度的指标。假设用于刻画模型在训练数据上表现的损失函数为J(θ),那么优化时不是直接优化J(θ),而是优化J(θ) + λR(w),其中R(w)刻画的是模型的复杂程度,λ表示模型复杂损失在总损失中的比例。
常用的正则化函数有L1正则化函数和L2正则化函数,
L1正则化:
R(w) = Ʃ|wj|
L2正则化:
R(w) = Ʃ|wj2|
Tensorflow中L1和L2正则化函数分别为:
tf.contrib.layers.l1_regularizer()
Tf.contrib.layers.l2_regularizer()
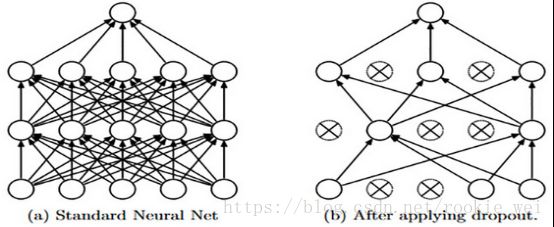
10.2 Dropout
避免过拟合问题,除了正则化,还有dropout,dropout在不同的训练过程中随机“丢掉”一部分神经元,让其不工作,但这个“丢掉”只是针对当前训练步骤的,让其在这次训练中不更新权值,也不参与这次的神经网络计算,下次训练时,这个神经元又可能工作。
前面《tensorflow学习笔记 两层卷积神经网络模型训练MNIST》例子就用到这个方法,
Tensorflow中,dropout函数为
tf.nn.dropout()
11、滑动平均模型
滑动平均模型可以使模型在测试数据上更加健壮。在采用随即梯度下降法训练神经网络时,使用滑动平均模型在很多应用中可以在一定程度上提高最终模型在测试数据上的表现。
tansorflow提供了tf.train.ExponentialMovingAverage来实现滑动平均模型。在初始化该函数时需要提供一个衰减率(decay),这个衰减率将用于控制模型更新的速度。decay决定了模型更新速度,decay越大,模型越趋于稳定,一般设置成非常接近1的数,比如0.999或0.9999。
如果您感觉本篇博客对您有帮助,请打开支付宝,领个红包支持一下,祝您扫到99元,谢谢~~
![]()