Face2Face: Real-time Face Capture and Reenactment of RGB Videos (CVPR 2016) 译文

建议的在线再现设置:单目目标视频序列(例如，来自Youtube)基于源演员的表达进行再现，源演员使用商品网络摄像头进行现场录制。

摘要

我们提出了一种用于单目目标视频序列(例如Youtube视频)的实时面部再现的新方法。源序列也是单目视频流，用商品网络摄像头实时捕获。我们的目标是通过源演员将目标视频的面部表情动画化，并以逼真的方式重新渲染被操纵的输出视频。为此，我们首先通过基于非刚性模型的捆绑解决了从单目视频中恢复面部身份的约束不足问题。在运行时，我们使用密集的光度一致性测量来跟踪源视频和目标视频的面部表情。然后通过在源和目标之间快速有效的变形传递来实现再现。从目标序列中检索与重新定位表达最匹配的口腔内部，并扭曲以产生准确的匹配。最后，我们令人信服地在相应的视频流上重新渲染合成的目标面，使其与现实世界的照明无缝融合。我们在现场设置中演示了我们的方法，其中Youtube视频是实时重演的。

1. 介绍

近年来，基于商品传感器的实时无标记面部行为捕获已经得到了验证。无论是基于RGB[8,6]还是RGB- d数据[31,10,21,4,16]，都取得了令人印象深刻的结果。这些技术在视频游戏和电影中的虚拟CG角色动画中越来越受欢迎。现在在家里运行这些面部捕捉和跟踪算法是可行的，这是许多VR和AR应用的基础，比如远程会议。

在本文中，我们采用了一种新的基于单目RGB数据的密集无标记面部性能捕获方法，类似于最先进的方法。然而，我们的主要贡献是实时的单目面部再现，而不是将面部表情转移到虚拟CG角色上。与之前离线运行的再现方法相反[5,11,13]，我们的目标是将RGB传感器捕获的源演员的面部表情在线转移到目标演员。目标序列可以是任意单目视频;例如，从Youtube下载的带有面部表演的遗留视频片段。我们的目标是以逼真的方式修改目标视频，这样几乎不可能注意到操纵。忠实逼真的面部再现是各种应用的基础;例如，在视频会议中，可以调整视频馈送以匹配翻译人员的面部动作，或者可以将面部视频令人信服地配音为外语。

在我们的方法中，我们首先使用基于预先录制的训练序列的新的全局非刚性模型捆绑方法重建目标演员的形状身份。由于该预处理是在一组训练帧上全局执行的，我们可以解决单眼重建中常见的几何模糊性。在运行时，我们通过基于统计面部先验的密集综合分析方法来跟踪源和目标演员视频的表情。我们证明，我们的RGB跟踪精度与最先进的水平相当，即使是依靠深度数据的在线跟踪方法。为了将表情从源实时传递到目标演员，我们提出了一种新的传递函数，该函数可以在使用的低维表达空间中直接有效地应用变形传递[27]。在最终的图像合成中，我们利用转移的表情系数重新渲染目标人脸，并考虑估计的环境光照与目标视频背景进行合成。最后，我们介绍了一种新的基于图像的口腔合成方法，该方法通过从离线样本序列中检索和扭曲最佳匹配的口腔形状来生成逼真的口腔内部。重要的是要注意，我们保持目标嘴型的外观;相比之下，现有的方法要么将源口腔区域复制到目标上[30,11]，要么渲染一个通用的牙齿代理[14,29]，这两种方法都会导致结果不一致。图1显示了我们方法的概述。

我们展示了高度令人信服的面部表情从源到目标视频的实时传输。我们通过现场设置显示结果，其中源视频流由网络摄像头捕获，用于操纵目标Youtube视频。此外，我们与最先进的再现方法进行了比较，我们在视频质量和运行时间方面都优于最先进的再现方法(我们是第一个实时RGB再现方法)。总之，我们的主要贡献是:

• 密集的，全局非刚性的基于模型的捆绑；
• 准确的跟踪，外观和照明估计在不受约束的实时RGB视频；
• 使用子空间变形的个体依赖表达转移;
• 一种新颖的口腔合成方法。

2. 相关工作

离线RGB性能捕获。最近的离线性能捕获技术通过将混合形状[15]或多线性面[26]模型拟合到输入视频序列来解决困难的单目重建问题。甚至几何精细尺度的表面细节提取通过逆阴影为基础的表面细化。Ichim等人[17]仅从单目输入构建了一个个性化的人脸钻机。他们从一个专门捕获的视频中执行静态头部的运动结构重建，并将其与身份和表达模型相匹配。个人特定的表达是从一个训练序列中学习的。Suwajanakorn等[28]从图像集合中学习身份模型，并基于模型到图像的流场跟踪面部动画。Shi等人[26]基于一组选定的关键帧的全局能量优化，取得了令人印象深刻的结果。我们用于恢复参与者身份的基于模型的捆绑公式与他们的方法相似;然而，我们使用鲁棒和密集的全局光度对齐，我们通过GPU上有效的数据并行优化策略来执行。

在线RGB-D性能捕获。Weise等人[32]通过将参数混合形状模型拟合到RGB-D数据来实时捕获面部性能，但他们需要专业的自定义捕获设置。Weise等人已经演示了基于商品深度传感器的第一个实时面部表现捕获系统[31]。后续工作[21,4,10,16]主要关注矫正形状[4]、动态适应blendshape基[21]、非刚性网格变形[10]以及对遮挡的鲁棒性[16]。这些作品取得了令人印象深刻的结果，但依赖于深度数据，这在大多数视频片段中通常是不可用的。

在线RGB性能捕获。虽然存在许多稀疏的实时面部跟踪器，例如[25]，但实时密集的单目跟踪是逼真的在线面部再现的基础。Cao等人[8]提出了一种基于实时回归的方法来推断面部地标的三维位置，这约束了用户特定的混合形状模型。后续研究[6]也对细尺度面部皱纹进行了回归。这些方法取得了令人印象深刻的结果，但不能直接应用于面部再现，因为它们不能促进密集的、像素精确的跟踪。

离线重演。Vlasic等[30]通过跟踪人脸模板进行人脸再现，人脸模板在目标对象上方以不同的表情参数进行再现;嘴巴内部直接从源视频复制。Dale等人[11]使用参数化模型取得了令人印象深刻的结果，但他们的目标是人脸替换，并在目标上组合源人脸。基于图像的离线口腔再动画方法见[5]。Garrido等[13]提出了一种完全基于图像的自动替换整个人脸的方法。这些方法只是使自我重演成为可能;即，当源和目标是同一个人时;相反，我们执行一个不同的目标演员的再现。最近的研究提出了虚拟配音[14]，这是一个类似于我们的问题;然而，该方法运行在缓慢的离线速率，并依赖于一个通用的牙齿代理口腔内部。Kemelmacher等[20]从大型图像集合中生成人脸动画，但获得的结果缺乏时间一致性。Li等人[22]基于相似性度量从数据库中检索帧。他们使用光流作为外观和速度测量，并根据时间戳和流距离搜索k个最近的邻居。Saragih等[25]提出了一种基于单幅图像的实时角色动画系统。他们的方法基于稀疏地标跟踪，并使用纹理扭曲将源口复制到目标。Berthouzoz等人[2]使用编码帧相似度的图上的最短路径搜索，为视频序列找到灵活的中间帧数。Kawai等[18]使用牙齿和舌头图像数据库重新合成给定正面2D动画的内口腔;他们仅限于正面的姿势，并不能产生像我们在一般头部运动下的逼真渲染。

在线重演。最近，首次提出了基于RGB-(D)数据的在线面部再现方法。Kemelmacher-Shlizerman等[19]通过从数据库中查询相似的图像来实现基于图像的木偶戏。他们采用外观成本度量并考虑旋转角距离，这与Kemelmacher等人[20]相似。虽然他们取得了令人印象深刻的结果，但检索到的人脸流在时间上并不连贯。Thies等[29]展示了第一个在线重演系统;然而，他们依赖于深度数据，并使用通用的牙齿代替口腔区域。在本文中，我们解决了这两个缺点:1)我们的方法是第一个实时rgb重现技术;2)我们完全从目标序列合成口腔区域(不需要牙齿代理或直接的源到目标复制)。

图1：方法概述

3. 面部图像的合成

我们使用基于[3,1,9]的多线性PCA模型。前两个维度代表面部身份——即几何形状和皮肤反射率——第三个维度控制面部表情。因此，我们将人脸参数化为:
$$\begin{array}{rl}{\mathcal{M}}_{\text{geo }}(\mathbf{\alpha },\mathbf{\delta })& ={\mathbf{a}}_{\mathrm{id}}+E_{\text{id }}\cdot \mathbf{\alpha }+E_{\text{exp }}\cdot \mathbf{\delta },\\ {\mathcal{M}}_{\text{alb }}(\mathbf{\beta })& ={\mathbf{a}}_{\text{alb }}+E_{\text{alb }}\cdot \mathbf{\beta }.\end{array}$$

该先验假设形状和反射率在平均形状附近的多元正态概率分布为 ${\mathbf{a}}_{\mathrm{id}}\in {\mathbb{R}}^{3n}$ ，反射率为 ${\mathbf{a}}_{\mathrm{alb}}\in {\mathbb{R}}^{3n}$ 。

给出了形状系数 $E_{\text{id }}\in {\mathbb{R}}^{3n\times 80}$ 、反射率 $E_{\text{alb }}\in {\mathbb{R}}^{3n\times 80}$ 和表情系数 $E_{\exp }\in {\mathbb{R}}^{3n\times 76}$ 基及其相应的标准差 ${\sigma }_{\text{id }}\in {\mathbb{R}}^{80},{\sigma }_{\text{alb }}\in {\mathbb{R}}^{80}$, and ${\sigma }_{\exp }\in {\mathbb{R}}^{76}$ 。该模型有53K个顶点和106K个面。在模型刚性变换 $\Phi (\mathbf{v})$ 和全透视变换 $\Pi (\mathbf{v})$ 下对模型进行栅格化，生成合成图像 $C_{\mathcal{S}}$ 。照明由球面谐波(Spherical Harmonics, SH)[23]基函数的前三个波段近似，假设Labertian曲面和光滑的远处照明，忽略自阴影。

合成依赖于人脸模型参数 $\alpha$, $\beta ,\delta$，照明参数 $\gamma$ ，刚性变换 $\mathbf{R},\mathbf{t}$ 和定义 $\Pi$ 的相机参数 $\mathbf{\kappa }$ 。未知向量 $\mathcal{P}$ 是这些参数的并集。

4. 能量公式

给定单目输入序列，我们用鲁棒变分优化联合重构所有未知参数P。所提出的目标在未知方面是高度非线性的，并具有以下组成部分:
$$E(\mathcal{P})=\underset{\text{data }}{w_{\text{col }}{E}_{\text{col }}(\mathcal{P})+w_{\text{lan }}{E}_{\text{lan }}(\mathcal{P})}+\underset{\text{prior }}{w_{\text{reg }}{E}_{\text{reg }}(\mathcal{P})}$$

数据项测量合成图像与输入数据在光一致性 $E_{col}$ 和面部特征对齐 $E_{lan}$ 方面的相似性。统计正则化器 $E_{reg}$ 考虑了给定参数向量 $\mathcal{P}$ 的似然性。权重 $w_{col}$, $w_{\text{lan }}$, 和 $w_{\text{reg }}$平衡了三个不同的子目标。在我们所有的实验中，我们设置$w_{\text{col }}=1,w_{\text{lan }}=10$, and $w_{\text{reg }}=2.5\cdot 10^{-5}$。下面，我们将介绍不同的子目标。

照片一致性。为了量化合成图像对输入数据的解释程度，我们测量了像素级的光度量对齐误差:
$$E_{\mathrm{col}}(\mathcal{P})=\frac{1}{|\mathcal{V}|}\sum _{\mathbf{p}\in \mathcal{V}}{\Vert C_{\mathcal{S}}(\mathbf{p})-C_{\mathcal{I}}(\mathbf{p})\Vert }_2$$

其中 $C_{\mathcal{S}}$ 为合成图像， $C_{\mathcal{I}}$ 为输入RGB图像，$\mathbf{p}\in \mathcal{V}$ 表示 $C_{\mathcal{S}}$ 中所有可见像素位置。我们使用 ${\ell }_{2,1}$ 范数[12]而不是最小二乘公式来对异常值具有鲁棒性。在我们的场景中，色彩空间中的距离基于 ${\ell }_2$ ，而在所有像素的总和中，使用 ${\ell }_1$ 范数来强制稀疏性。

特征对齐。此外，我们在RGB流中检测到的一组显著面部特征点对之间强制特征相似性:
$$E_{\text{lan }}(\mathcal{P})=\frac{1}{|\mathcal{F}|}\sum _{{\mathbf{f}}_j\in \mathcal{F}}{w}_{\text{conf },j}\Vert {\mathbf{f}}_j-\Pi (\Phi \left({\mathbf{v}}_j\right){\Vert }_2^2.$$

为此，我们采用了一种最先进的面部地标跟踪算法[24]。每个特征点 ${\mathbf{f}}_j\in \mathcal{F}\subset$ ${\mathbb{R}}^2$ 都有一个检测置信度$w_{\text{conf },j}$ ，并对应一个唯一的顶点 ${\mathbf{v}}_j={\mathcal{M}}_{\text{geo }}(\mathbf{\alpha },\mathbf{\delta })\in {\mathbb{R}}^3$ 的先验值。这有助于避免在 $E_{\text{col }}(\mathcal{P})$ 高度复杂的能量格局中出现局部极小值。

统计正规化。基于正态分布总体的假设，我们增强了合成人脸的可信性。为此，我们强制参数保持在统计上接近平均值:
$$E_{\mathrm{reg}}(\mathcal{P})=\sum _{i=1}^{80}\left[{\left(\frac{{\mathbf{\alpha }}_i}{{\sigma }_{\mathrm{id},i}}\right)}^2+{\left(\frac{{\mathbf{\beta }}_i}{{\sigma }_{\mathrm{alb},i}}\right)}^2\right]+\sum _{i=1}^{76}{\left(\frac{{\mathbf{\delta }}_i}{{\sigma }_{\exp ,i}}\right)}^2.$$

这种常用的正则化策略防止了面部几何和反射率的退化，并引导优化策略走出局部最小值[3]。

5. 数据并行优化策略

所提出的鲁棒跟踪目标是一个一般的无约束非线性优化问题。我们使用一种新颖的基于数据并行gpu的迭代重加权最小二乘(IRLS)求解器实时最小化该目标。IRLS的关键思想是，在每次迭代中，通过将范数分成两个部分，将问题转化为非线性最小二乘问题:
$$\Vert r(\mathcal{P}){\Vert }_2=\underset{\text{constant }}{{\left({\Vert r\left({\mathcal{P}}_{\text{old }}\right)\Vert }_2\right)}^{-1}}\cdot \Vert r(\mathcal{P}){\Vert }_2^2.$$
其中，$r(\cdot )$ 为一般残差，${\mathcal{P}}_{\text{old }}$ 为上次迭代计算的解。因此，第一部分在一次迭代期间保持不变，然后更新。与[29]相似，每个迭代步骤都是使用高斯-牛顿方法实现的。我们在每次IRLS迭代中采用单个GN步骤，求解相应的基于PCG的正规方程组 ${\mathbf{J}}^T\mathbf{J}{\mathbf{\delta }}^{\ast }=-{\mathbf{J}}^T\mathbf{F}$ ，以获得最优的线性参数更新 ${\mathbf{\delta }}^{\ast }$ 。按照Thies等人的建议[29]，预先计算雅可比矩阵 $\mathbf{J}$ 和系统右侧的 $-{\mathbf{J}}^T\mathbf{F}$ 并存储在设备存储器中供以后处理。根据[33,29]的建议，我们将PCG求解器中的旧下降方向 $\mathbf{d}$ 与系统矩阵 ${\mathbf{J}}^T\mathbf{J}$ 的乘法拆分为两个连续的矩阵向量积。关于优化框架的附加细节在补充材料中提供。

6. 非刚性基于模型的捆绑

为了在严重欠约束的单目重建场景中估计参与者的身份，我们引入了一种基于非刚性模型的捆绑方法。基于提出的目标，我们对输入视频序列的k个关键帧的所有参数进行了联合估计。估计的未知数是全局恒等式 $\{\mathbf{\alpha },\mathbf{\beta }\}$ 和本征因子 $\mathbf{\kappa }$ ，以及未知的每帧姿态 $\{{\mathbf{\delta }}^k$, ${{\mathbf{R}}^k,{\mathbf{t}}^k\}}_k$ 和照明参数 ${\left\{{\mathbf{\gamma }}^k\right\}}_k$ 。我们使用与模型到帧跟踪类似的数据并行优化策略，但联合求解整个关键帧集的法向方程。对于基于非刚性模型的捆绑问题，对应的雅可比矩阵的非零结构是块密集的。我们的PCG求解器利用非零结构来提高性能(参见附加文档)。由于所有关键帧在可能不同的光照、表情和视角下观察到相同的面部身份，因此我们可以将身份从所有其他问题维度中稳健地分离出来。请注意，我们还求解了 $\Pi$ 的固有相机参数，因此能够处理未校准的视频片段。

7. 表情迁移

为了将表情变化从源转移到目标演员，同时保持每个演员表情的个性，我们提出了一种子空间变形转移技术。我们受到Sumner等人[27]的变形传递能量的启发，但直接在表达式blendshapes所跨越的空间中进行操作。这不仅允许预先计算系统矩阵的伪逆，而且还大大降低了优化问题的维数，从而实现快速的实时传输速率。假设源单位 ${\mathbf{\alpha }}^S$ 和目标单位 ${\mathbf{\alpha }}^T$ 固定，传递以中性 ${\mathbf{\delta }}_N^S$ 、变形源 ${\mathbf{\delta }}^S$ 和中性目标 ${\mathbf{\delta }}_N^T$ 表情为输入。输出是直接在参数先验的约简子空间中传递的面部表情 ${\delta }^T$ 。

根据[27]的建议，我们首先计算源变形梯度 ${\mathbf{A}}_i\in {\mathbb{R}}^{3\times 3}$ ，将源三角形从中性转换为变形。变形靶 ${\hat{\mathbf{v}}}_i={\mathbf{M}}_i\left({\mathbf{\alpha }}^T,{\mathbf{\delta }}^T\right)$ ;然后根据未变形状态${\mathbf{v}}_i=M_i\left({\mathbf{\alpha }}^T,{\delta }_N^T\right)$ ;通过求解线性最小二乘问题。令 $\left(i_0,i_1,i_2\right)$ 为第i个三角形的顶点指标，$\mathbf{V}=\left[{\mathbf{v}}_{i_1}-{\mathbf{v}}_{i_0},{\mathbf{v}}_{i_2}-{\mathbf{v}}_{i_0}\right]$ 和$\hat{\mathbf{V}}=\left[{\mathbf{v}}_{i_1}-{\hat{\mathbf{v}}}_{i_0},{\hat{\mathbf{v}}}_{i_2}-{\hat{\mathbf{v}}}_{i_0}\right]$，则未知目标最优变形 ${\delta }^T$ 最小值为:

E ( δ T ) = ∑ i = 1 ∣ F ∣ ∥ A i V − V ^ ∥ F 2 . E\left(\boldsymbol{\delta}^T\right)=\sum_{i=1}^{|\boldsymbol{F}|}\left\|\mathbf{A}_i \mathbf{V}-\hat{\mathbf{V}}\right\|_F^2 . E(δT)=i=1∑∣F∣​ ​Ai​V−V^ ​F2​.
这个问题可以通过代入改写成标准最小二乘形式::
E ( δ T ) = ∥ A δ T − b ∥ 2 2 . E\left(\boldsymbol{\delta}^T\right)=\left\|\mathbf{A} \boldsymbol{\delta}^T-\boldsymbol{b}\right\|_2^2 . E(δT)= ​AδT−b ​22​.

矩阵 $\mathbf{A}\in {\mathbb{R}}^{6|\mathbf{F}|\times 76}$ 为常数，包含模板网格投影到表达式子空间的边缘信息。中性表达式中目标的边缘信息包含在右侧$\mathbf{b}\in {\mathbb{R}}^{6|\mathbf{F}|}$. $\mathbf{b}$ 中。 $\mathbf{b}$ 随 ${\delta }^S$ 变化，并在GPU上为每个新的输入帧计算。二次能量的最小值可以通过求解相应的法向方程来计算。由于系统矩阵是常数，我们可以使用奇异值分解(SVD)来预先计算它的伪逆。随后，对小型76 × 76线性系统进行了实时求解。不需要像[27,4]中那样额外的平滑项，因为blendshape模型隐式地将结果限制为合理的形状并保证平滑。

图2:嘴巴检索:我们使用一个外观图来检索新的嘴巴框架。为了选择一个帧，我们在最小化到目标表达式的距离的同时，强制与先前检索的帧相似。

8. 嘴唇检索

对于一个给定的面部表情，我们需要合成一个逼真的目标嘴区。为此，我们从目标演员序列中检索和扭曲最匹配的嘴巴图像。我们假设目标视频中有足够的口型变化。同样重要的是要注意我们保持目标嘴的外观。这比复制源口腔区域[30,11]或使用通用的3D牙齿代理[14,29]产生更真实的结果。

我们的方法首先基于一种新的特征相似度度量的帧到簇匹配策略找到最适合的目标嘴帧。为了加强时间一致性，我们使用密集的外观图来找到最后检索的嘴帧和目标嘴帧之间的折衷(参见图2)。我们在下面详细介绍了所有步骤。

相似性度量。我们的相似性度量基于几何和光度特征。使用的描述符 $\mathcal{K}=\{\mathbf{R},\mathbf{\delta },\mathcal{F},\mathcal{L}\}$ 一帧由旋转R、表达参数 $\mathbf{\delta }$, 、地标 $\mathcal{F}$ 和局部二值模式(LBP) $\mathcal{L}$ 组成，我们为训练序列中的每一帧计算这些描述子 ${\mathcal{K}}^S$ 。目标描述符 ${\mathcal{K}}^T$ 由表达转移的结果和驱动行为体框架的LBP组成。我们测量源描述符和目标描述符之间的距离如下:
$$D\left({\mathcal{K}}^T,{\mathcal{K}}_t^S,t\right)=D_p\left({\mathcal{K}}^T,{\mathcal{K}}_t^S\right)+D_m\left({\mathcal{K}}^T,{\mathcal{K}}_t^S\right)+D_a\left({\mathcal{K}}^T,{\mathcal{K}}_t^S,t\right)$$

第一项 $D_p$ 表示参数空间中的距离:
D p ( K T , K t S ) = ∥ δ T − δ t S ∥ 2 2 + ∥ R T − R t S ∥ F 2 . D_p\left(\mathcal{K}^T, \mathcal{K}_t^S\right)=\left\|\boldsymbol{\delta}^T-\boldsymbol{\delta}_t^S\right\|_2^2+\left\|\mathbf{R}^T-\mathbf{R}_t^S\right\|_F^2 . Dp​(KT,KtS​)= ​δT−δtS​ ​22​+ ​RT−RtS​ ​F2​.
第二项 $D_m$ 测量稀疏面部标志的差分兼容性:
D m ( K T , K t S ) = ∑ ( i , j ) ∈ Ω ( ∥ F i T − F j T ∥ 2 − ∥ F t , i S − F t , j S ∥ 2 ) 2 D_m\left(\mathcal{K}^T, \mathcal{K}_t^S\right)=\sum_{(i, j) \in \Omega}\left(\left\|\mathcal{F}_i^T-\mathcal{F}_j^T\right\|_2-\left\|\mathcal{F}_{t, i}^S-\mathcal{F}_{t, j}^S\right\|_2\right)^2 Dm​(KT,KtS​)=(i,j)∈Ω∑​( ​FiT​−FjT​ ​2​− ​Ft,iS​−Ft,jS​ ​2​)2
这里， $\Omega$ 是一组预定义的地标对，定义了上唇和下唇之间或嘴角左右之间的距离。最后一项 $D_a$ 是外观测量项，由两部分组成:
$$D_a\left({\mathcal{K}}^T,{\mathcal{K}}_t^S,t\right)=D_l\left({\mathcal{K}}^T,{\mathcal{K}}_t^S\right)+w_c\left({\mathcal{K}}^T,{\mathcal{K}}_t^S\right)D_c(\tau ,t).$$
$\tau$ 是用于前一帧中的再现的最后检索的帧索引。$D_l\left({\mathcal{K}}^T,{\mathcal{K}}_t^S\right)$ 基于通过卡平方距离比较的 LBPs 来测量相似性(详细信息参见[13])。直流 $D_c(\tau ,t)$ 基于归一化口帧的RGB互相关度量最后检索到的帧 $\tau$ 与视频帧 $t$ 之间的相似性。请注意，嘴巴帧是基于模型纹理参数化进行归一化的(参见图2)。为了促进表情变化的快速帧跳转，我们将权重 $w_c\left({\mathcal{K}}^T,{\mathcal{K}}_t^S\right)=e^{-{\left(D_m\left({\mathcal{K}}^T,{\mathcal{K}}_t^S\right)\right)}^2}$ 。我们将这种帧到帧的距离测量应用到帧到集群的匹配策略中，从而实现实时速率并减轻嘴帧之间的高频跳变。

单帧到组的匹配。利用提出的相似性度量，我们使用基于成对距离函数d的改进k-means算法将目标演员序列聚为 $k=10$ 个聚类，对于每个聚类，我们选择与该聚类中所有其他帧距离最小的帧作为代表。在运行时，我们测量目标描述符 ${\mathcal{K}}^T$ 与集群代表描述符之间的距离，并选择代表帧距离最小的集群作为新的目标帧。

外观图。我们通过建立所有视频帧的完全连接的外观图来提高时间一致性。边的权值是基于RGB规范化嘴唇之间的互相关帧,在参数空间 $D_p$的距离,地标 $D_m$ 距离。图的距离使我们能够找到一个中间画框架既类似于上次检索框架和检索目标框架(见图2)。我们计算这个完美匹配,发现训练序列的帧,最小化边的权值之和最后检索和当前帧目标。在光流对齐后，我们在纹理空间中以像素级将先前检索到的帧与新检索到的帧进行融合。在混合之前，我们应用光照校正，该校正考虑了检索帧和当前视频帧的估计球谐光照参数。最后，我们通过在原始视频帧、经过光照校正的投影嘴帧和渲染的人脸模型之间进行alpha混合来合成新的输出帧。

9. 结果

实时人脸重演准备。我们的现场再现设置由标准的消费者级硬件组成。我们用一个普通的网络摄像头(源)捕捉实时视频，并从Youtube(目标)下载单目视频剪辑。在我们的实验中，我们使用罗技HD Pro C920相机，运行在30Hz，分辨率为640 × 480;尽管我们的方法适用于任何消费类RGB相机。总体而言，我们以1280×720的分辨率在各种目标Youtube视频上展示了我们算法的高度逼真的再现示例。这些视频展示了从不同角度拍摄的不同场景中的不同主体;每个视频都由几名志愿者作为源演员重新播放。再现结果以1280 × 720的分辨率生成。我们在图8和附带的视频中显示了实时再现结果。

运行时间。对于所有的实验，我们使用三个层次来跟踪(源和目标)。在位姿优化中，我们只考虑第二层和第三层，分别运行一个和七个高斯-牛顿步。在高斯-牛顿步骤中，我们总是运行四个PCG步骤。除了跟踪之外，我们的重现管道还有额外的阶段，其时间安排列在表1中。我们的方法在一台配备NVIDIA Titan X和Intel Core i7-4770的普通台式计算机上实时运行。

与以前工作的跟踪比较。面部跟踪本身并不是我们工作的主要重点，但下面的比较表明，我们的跟踪已经达到或超过了最先进的水平。

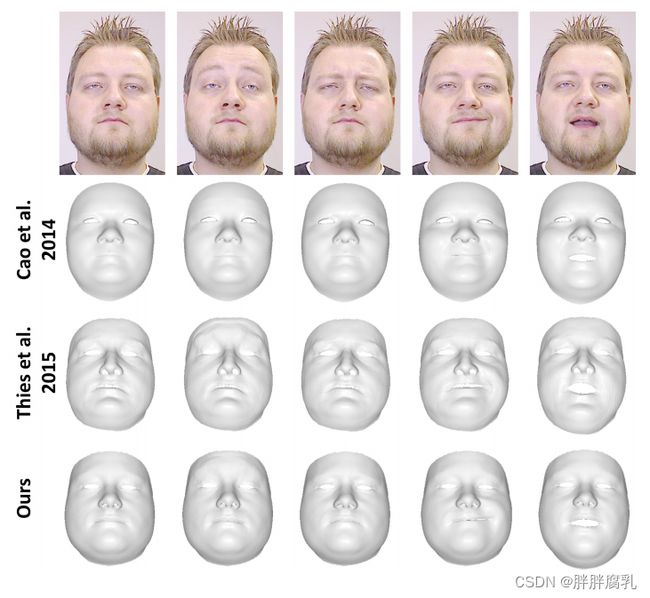
图3：我们的RGB跟踪与 Cao et al. [7] 和 Thies et al. [29] 的RGB- d跟踪的比较。

图4: 我们与 Shi et al. [26] 的跟踪对比。从左到右:RGB输入，重建模型，叠加输入，眼睛和脸颊特写。请注意，Shi等人在后期处理中执行形状-从阴影。

图5: 与facshift RGB-D跟踪的比较。

图6: 配音:与 Garrido et al. [14] 的对比[14]。

Shi et al. 2014 [26]: 他们从单目无约束RGB视频中脱机捕捉人脸行为。图4中的特写显示，我们的在线方法产生了更接近的面部匹配，特别是在输入面部的轮廓处可见。我们相信我们的新密集非刚性束调整导致比他们的稀疏方法更好的形状同一性估计。

Cao et al. 2014 [7]: 通过单目RGB实时捕捉人脸表现。在大多数情况下，我们和他们的方法产生相似的高质量结果(见图3);不过，我们对身份和表情的估计要稍微准确一些。

Thies et al. 2015 [29]: 他们的方法从RGB-D实时捕获面部表现，图3。两种方法的结果同样准确;但我们的方法不需要深度数据。

FaceShift 2014: 我们将我们的跟踪器与facshift的商业实时RGB-D跟踪器进行比较，该跟踪器基于Weise等人[31]的工作。图5显示，我们只使用RGB得到类似的结果。

人脸重现评价。在图6中，我们将我们的方法与Garrido等人[14]的最先进的再现法进行了比较。这两种方法都提供了高度逼真的再现结果;然而，他们的方法基本上是离线的，因为他们需要在任何时候出现一个序列的所有帧。此外，它们依赖于一个通用的几何牙齿代理，这在某些帧使再现不那么令人信服。在图7中，我们与Thies等人[29]的工作进行了比较。两种方法的运行时间和视觉质量是相似的;然而，他们的几何牙齿代理导致不希望的外观变化，在口腔重现。此外，Thies等人使用RGB-D相机，这限制了应用范围;他们不能重现Youtube视频。我们在补充材料中对Dale等人[11]和Garrido等人[13]进行了进一步的比较。

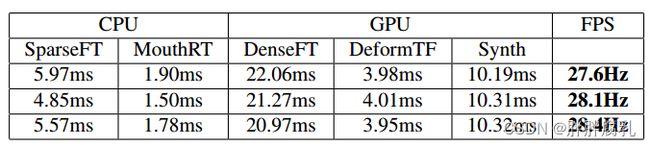
表1:图8中三个序列的平均运行时间，从上到下。最终帧率的标准偏差分别为0.51,0.56和0.59 fps。请注意，CPU和GPU阶段并行运行。

图8: 再现系统的结果。表1列出了相应的运行时间。所述源序列和所得到的输出序列的长度分别为965、1436和1791帧;输入目标序列的长度分别为431帧、286帧和392帧。

10. 局限性

朗伯曲面和光滑照明的假设是有限的，并可能导致在硬阴影或高光存在的人工制品;这是大多数最先进的方法所共有的限制。长头发和胡须遮挡脸部的场景很有挑战性。此外，我们只重建和跟踪一个低维混合形状模型(76个表达式系数)，忽略了精细尺度的静态和瞬态表面细节。我们基于检索的口腔合成假设在目标序列中有足够的可见表达变化。在一个太短的序列中，或者当目标保持静止时，我们无法学习个人特定的嘴部行为。在这种情况下，可以观察到时间混叠，因为检索到的口腔样本的目标空间过于稀疏。另一个限制是由我们的硬件设置(网络摄像头，USB和PCI)引起的，它引入了≈3帧的小延迟。专门的硬件可以解决这个问题，但我们的目标是使用普通硬件进行设置。

11. 结论

我们提出的方法是第一个实时面部再现系统，只需要单目RGB输入。我们的现场设置使遗留视频片段的动画-例如，从Youtube -在实时。总的来说，我们相信我们的系统将为VR/AR、电话会议或带有翻译音频的视频实时配音等领域的许多新的令人兴奋的应用铺平道路。

参考

[1] O. Alexander, M. Rogers, W. Lambeth, M. Chiang, and P. Debevec. The Digital Emily Project: photoreal facial modeling and animation. In ACM SIGGRAPH Courses, pages 12:1–12:15. ACM, 2009.
[2] F. Berthouzoz, W. Li, and M. Agrawala. Tools for placing cuts and transitions in interview video. ACM TOG, 31(4):67, 2012.
[3] V. Blanz and T. Vetter. A morphable model for the synthesis of 3d faces. In Proc. SIGGRAPH, pages 187–194. ACM Press/Addison-Wesley Publishing Co., 1999.
[4] S. Bouaziz, Y. Wang, and M. Pauly. Online modeling for realtime facial animation. ACM TOG, 32(4):40, 2013.
[5] C. Bregler, M. Covell, and M. Slaney. Video rewrite: Driving visual speech with audio. In Proc. SIGGRAPH, pages 353–360. ACM Press/Addison-Wesley Publishing Co., 1997.
[6] C. Cao, D. Bradley, K. Zhou, and T. Beeler. Real-time highfidelity facial performance capture. ACM TOG, 34(4):46:1–46:9, 2015.
[7] C. Cao, Q. Hou, and K. Zhou. Displaced dynamic expression regression for real-time facial tracking and animation. ACM TOG, 33(4):43, 2014.
[8] C. Cao, Y. Weng, S. Lin, and K. Zhou. 3D shape regression for real-time facial animation. ACM TOG, 32(4):41, 2013.
[9] C. Cao, Y. Weng, S. Zhou, Y. Tong, and K. Zhou. Facewarehouse: A 3D facial expression database for visual computing. IEEE TVCG, 20(3):413–425, 2014.
[10] Y.-L. Chen, H.-T. Wu, F. Shi, X. Tong, and J. Chai. Accurate and robust 3d facial capture using a single rgbd camera. Proc. ICCV, pages 3615–3622, 2013.
[11] K. Dale, K. Sunkavalli, M. K. Johnson, D. Vlasic, W. Matusik, and H. Pfister. Video face replacement. ACM TOG, 30(6):130, 2011.
[12] C. H. Q. Ding, D. Zhou, X. He, and H. Zha. R1-pca: rotational invariant l1-norm principal component analysis for robust subspace factorization. In W. W. Cohen and A. Moore, editors, ICML, volume 148 of ACM International Conference Proceeding Series, pages 281–288. ACM, 2006.
[13] P. Garrido, L. Valgaerts, O. Rehmsen, T. Thormaehlen, P. Perez, and C. Theobalt. Automatic face reenactment. In Proc. CVPR, 2014.
[14] P. Garrido, L. Valgaerts, H. Sarmadi, I. Steiner, K. Varanasi, P. Perez, and C. Theobalt. Vdub: Modifying face video of actors for plausible visual alignment to a dubbed audio track. In Computer Graphics Forum. Wiley-Blackwell, 2015.
[15] P. Garrido, L. Valgaerts, C. Wu, and C. Theobalt. Reconstructing detailed dynamic face geometry from monocular video. ACM TOG, 32(6):158, 2013.
[16] P.-L. Hsieh, C. Ma, J. Yu, and H. Li. Unconstrained realtime facial performance capture. In Computer Vision and Pattern Recognition (CVPR), 2015.
[17] A. E. Ichim, S. Bouaziz, and M. Pauly. Dynamic 3d avatar creation from hand-held video input. ACM TOG, 34(4):45:1–45:14, 2015.
[18] M. Kawai, T. Iwao, D. Mima, A. Maejima, and S. Morishima. Data-driven speech animation synthesis focusing on realistic inside of the mouth. Journal of Information Processing, 22(2):401–409, 2014.
[19] I. Kemelmacher-Shlizerman, A. Sankar, E. Shechtman, and S. M. Seitz. Being john malkovich. In Computer Vision- ECCV 2010, 11th European Conference on Computer Vision, Heraklion, Crete, Greece, September 5-11, 2010, Proceedings, Part I, pages 341–353, 2010.
[20] I. Kemelmacher-Shlizerman, E. Shechtman, R. Garg, and S. M. Seitz. Exploring photobios. ACM TOG, 30(4):61, 2011.
[21] H. Li, J. Yu, Y. Ye, and C. Bregler. Realtime facial animation with on-the-fly correctives. ACM TOG, 32(4):42, 2013.
[22] K. Li, F. Xu, J. Wang, Q. Dai, and Y. Liu. A data-driven approach for facial expression synthesis in video. In Proc. CVPR, pages 57–64, 2012.
[23] R. Ramamoorthi and P. Hanrahan. A signal-processing framework for inverse rendering. In Proc. SIGGRAPH, pages 117–128. ACM, 2001.
[24] J. M. Saragih, S. Lucey, and J. F. Cohn. Deformable model fitting by regularized landmark mean-shift. IJCV, 91(2):200–215, 2011.
[25] J. M. Saragih, S. Lucey, and J. F. Cohn. Real-time avatar animation from a single image. In Automatic Face and Gesture Recognition Workshops, pages 213–220, 2011.
[26] F. Shi, H.-T. Wu, X. Tong, and J. Chai. Automatic acquisition of high-fidelity facial performances using monocular videos. ACM TOG, 33(6):222, 2014.
[27] R. W. Sumner and J. Popovic. Deformation transfer for triangle meshes. ACM TOG, 23(3):399–405, 2004.
[28] S. Suwajanakorn, I. Kemelmacher-Shlizerman, and S. M. Seitz. Total moving face reconstruction. In Proc. ECCV, pages 796–812, 2014.
[29] J. Thies, M. Zollhofer, M. Nießner, L. Valgaerts, M. Stam-minger, and C. Theobalt. Real-time expression transfer for facial reenactment. ACM Transactions on Graphics (TOG), 34(6), 2015.
[30] D. Vlasic, M. Brand, H. Pfister, and J. Popovic. Face transfer with multilinear models. ACM TOG, 24(3):426–433, 2005.
[31] T. Weise, S. Bouaziz, H. Li, and M. Pauly. Realtime performance-based facial animation. 30(4):77, 2011.
[32] T. Weise, H. Li, L. V. Gool, and M. Pauly. Face/off: Live facial puppetry. In Proceedings of the 2009 ACM SIGGRAPH/Eurographics Symposium on Computer animation (Proc. SCA’09), ETH Zurich, August 2009. Eurographics Association.
[33] M. Zollhofer, M. Nießner, S. Izadi, C. Rehmann, C. Zach, ¨M. Fisher, C. Wu, A. Fitzgibbon, C. Loop, C. Theobalt, and M.Stamminger. Real-time Non-rigid Reconstruction using an RGB-D Camera. ACM TOG, 33(4):156, 2014.