直方图均衡化-从公式到代码（python）

1.直方图均衡化理论

1.1 直方图均衡化介绍

1.1.1直方图均衡化的介绍

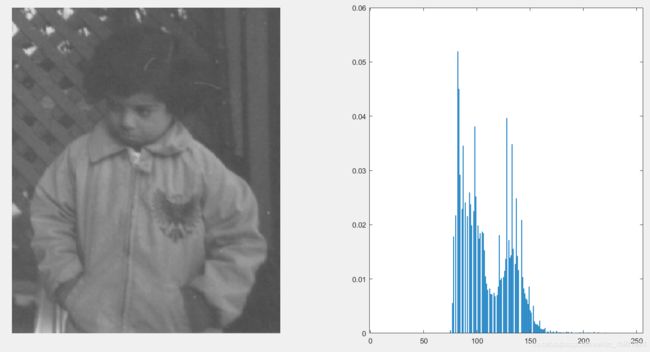
直方图均衡化是一种简单有效的图像增强技术，通过改变图像的直方图来改变图像中各像素的灰度，主要用于增强动态范围偏小的图像的对比度。原始图像由于其灰度分布可能集中在较窄的区间，造成图像不够清晰。例如，过曝光图像的灰度级集中在高亮度范围内，而曝光不足将使图像灰度级集中在低亮度范围内。采用直方图均衡化，可以把原始图像的直方图变换为均匀分布（均衡）的形式，这样就增加了像素之间灰度值差别的动态范围，从而达到增强图像整体对比度的效果。换言之，直方图均衡化的基本原理是：对在图像中像素个数多的灰度值（即对画面起主要作用的灰度值）进行展宽，而对像素个数少的灰度值（即对画面不起主要作用的灰度值）进行归并，从而增大对比度，使图像清晰，达到增强的目的。举个例子，如图1所示，左图为原始图像，右图为直方图均衡化后的图像。

图1

1.1.2直方图的概念

对一幅灰度图像，其直方图反映了该图像中不同灰度级出现的统计情况。图2给出了一个直方图的示例，其中图(a)是一幅图像，其灰度直方图可表示为图(b)，其中横轴表示图像的各灰度级，纵轴表示图像中各灰度级像素的个数。（需要注意，灰度直方图表示了在图像中各个单独灰度级的分布，而图像对比度则取决于相邻近像素之间灰度级的关系。）

#opencv 绘制直方图
import cv2
img = cv2.imread('img.jpg')
hist = cv2.calcHist([img],[0],None,[256],[0,256])
#numpy  绘制直方图
import numpy as np
hist，bins = np.histogram（img.ravel（），256，[0,256]）
hist = np.bincount（img.ravel（），minlength = 256）
#matplotlib 绘制直方图
from matplotlib import pyplot as plt
plt.hist(img,256,[0,256])
plt.show()

严格地说，图像的灰度直方图是一个一维的离散函数，可写成：

$$h(k)=n_k其中k=0,1,...,L-1（公式1）$$

式中，$n_k$是图像f(x,y)中灰度级为k的像素的个数。直方图的每一列（称为bin）的高度对应$n_k$。直方图提供了原图中各种灰度值分布的情况，也可以说直方图给出了一幅图像所有灰度值的整体描述。直方图的均值和方差也是图像灰度的均值和方差。图像的视觉效果与其直方图有对应关系，或者说，直方图的形状和改变对图像有很大的影响。

在直方图的基础上，进一步定义归一化的直方图为灰度级出现的相对频率$P_r(k)$。即：

$$P_r(k)=n_k/N（公式2）$$

式中，N表示图像f(x,y)的像素的总数，$n_k$是图像f(x,y)中灰度级为k的像素的个数。

我们以图1中左图为例，计算其归一化的直方图，结果如图4所示。

1.1.3直方图均衡化的理论基础

为讨论方便起见，以 r 和 s 分别表示归一化了的原图像灰度和经直方图均衡化后的图像灰度（因为归一化了，所以 r 和 s 的取值在0到1之间）。当 r = s = 0时，表示黑色；当 r = s = 1时，表示白色；当 r, s ∈(0, 1)时，表示像素灰度在黑白之间变化。（所谓直方图均衡化，其实是根据直方图对像素点的灰度值进行变换，属于点操作范围。换言之，即：已知r，求其对应的s。）

在 [0,1] 区间内的任何一个 r ，经变换函数 T( r ) 都可以产生一个对应的 s ，且

$$s=T(r)（公式3）$$

式中，T® 应当满足以下两个条件：

在 0 ≤ r ≤ 1 内，T ( r) 为单调递增函数；（此条件保证了均衡化后图像的灰度级从黑到白的次序不变）
在 0 ≤ r ≤ 1 内有 0 ≤ T( r) ≤ 1。（此条件保证了均衡化后图像的像素灰度值在允许的范围内）
公式3的逆变换关系为：
$$r=T^{-1}(s)（公式4）$$
式中，$T^{-1}(s)$对 s 同样满足上述的两个条件。

由概率论可知，如果已知随机变量 r 的概率密度是 $p_r(r)$，而随机变量 s 是 r 的函数，则 s 的概率密度$p_s(s)$可以由$p_r(r)$ 求出。假定随机变量 s 的分布函数用 $F_s(s)$ 表示，根据分布函数的定义有
$$F_s(s)={\int }_{-\infty }^s{p}_s(s)ds={\int }_{-\infty }^r{p}_r(r)dr（公式5）$$
又因为概率密度函数是分布函数的导数，因此公式5两边对 s 求导可得：
$$p_s(s)=\frac{\mathrm{d}{F}_s(s)}{\mathrm{d}s}=\frac{\mathrm{d}\left[{\int }_{-\infty }^r{p}_r(r)dr\right]}{\mathrm{d}s}=p_r(r)\frac{\mathrm{d}r}{\mathrm{d}s}=p_r(r)\frac{dr}{d[T(r)]}（公式6）$$
从公式6可以看出，通过变换函数 T( r) 可以控制图像灰度级的概率密度函数 $p_s(s)$，从而改善图像的灰度层次，这就是直方图均衡化的理论基础。

又有：从人眼视觉特性来考虑，一幅图像的灰度直方图如果是均匀分布的，那么该图像看上去效果比较好（参考冈萨雷斯数字图像处理3.3节）。因此要做直方图均衡化，这里的 $p_s(s)$ 应当是均匀分布的概率密度函数。

由概率论知识可知，对于区间 [a,b]上的均匀分布，其概率密度函数等于 $\frac{1}{b-a}$。 如果原图像没有进行归一化，即 $r\in [0,L-1]$, 那么$p_s(s)=\frac{1}{(L-1)-0}=\frac{1}{L-1}$，归一化之后 $r\in [0,1]$，所以这里的 $p_s(s)=\frac{1}{1-0}=1$。

由公式6可以知道$p_s(s)ds=p_r(r)dr$，又因为 $p_s(s)=1$ ，所以有 $ds=p_r(r)dr$。对这个式子两边积分得：
$$s=T(r)={\int }_0^r{p}_r(r)dr（公式7）$$

公式7就是我们所求的变换函数 T( r)。它表明当变换函数 T( r) 是原图像直方图的累积分布概率时，能达到直方图均衡化的目的。

对于灰度级为离散的数字图像，用频率来代替概率，则变换函数 $T(r_k)$ 的离散形式可以表示为：
$$s_k=T(r_k)=\sum _{i=0}^k{p}_r(r_i)=\sum _{i=0}^k\frac{n_i}{N}（公式8）$$
式中，$0⩽r_k⩽1,k=0,1,2,...,L-1$（注：这里的 $r_k=\frac{k}{L-1}$，表示归一化后的灰度级；k表示归一化前的灰度级）。由公式8可以知道，均衡化后各像素的灰度级 $s_k$ 可直接由原图像的直方图算出来。需要说明的是，这里的 $s_k$ 也是归一化后的灰度级，其值在 0 到 1 之间；有时需要将其乘以L-1再取整，使其灰度级范围在 0 到 L-1之间，与原图像一致。

1.2 直方图均衡化步骤

1.2.1 手工实现直方图均衡化

了解直方图均衡化的原理之后，我们以一个简单的例子来手工计算均衡化后的图像。这里我们假设存在以下这张图像（假定图像的灰度级范围是 [0, 9]）：

图 5 原始图像
计算过程如下：

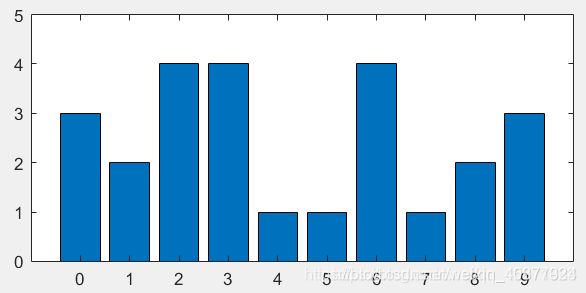
第一步，计算原始图像的灰度直方图 $n_k$。

n(0) = 3，即原始图像中灰度级为0的像素的个数是3，直接从图5中可以数出来。按这样的方式分别得出 n(1), n(2), …, n(9)。这里我们可以得到 $n_k$= [3,2,4,4,1,1,4,1,2,3]。

图 6 原始图像的灰度直方图
第二步，计算原始图像的像素总个数。

这里 N = 5*5 = 25。

第三步，计算原始图像的灰度分布频率。

p_{r}(k) = n_{k} / N = [3/25,2/25,4/25,4/25,1/25,1/25,4/25,1/25,2/25,3/25]，k = 0, 1, 2, …, 9

第四步，计算原始图像的灰度累积分布频率。
$$s_k=\sum _{i=0}^k\frac{n_i}{N}=[3/25,5/25,9/25,13/25,14/25,15/25,19/25,20/25,22/25,25/25]，k=0,1,2,...,9$$
第五步，将归一化的 s_{k} 乘以 L-1再四舍五入，以使得均衡化后图像的灰度级与归一化前的原始图像一致。

$s_0=\frac{3}{25}\ast (L-1)=\frac{3}{25}\ast 9=1.08$，四舍五入之后其值为1，也就是说原始图像中灰度级0对应均衡化后的灰度级1，即0→1。

同理，$s_1$ = 1.8，四舍五入之后为2，即1→2；$s_2$ = 3.24，四舍五入之后为3，即2→3；$s_3$ = 4.68，四舍五入之后为5，即3→5；$s_4$ = 5.04，四舍五入之后为5，即4→5；$s_5$ = 5.4，四舍五入之后为5，即5→5；$s_6$ = 6.84，四舍五入之后为7，即6→7；$s_7$ = 7.2，四舍五入之后为7，即7→7；$s_8$ = 7.92，四舍五入之后为8，即8→8；$s_9$ = 9，四舍五入之后为9，即9→9。

以上的映射关系，就是变换函数 T( r) 的作用。

第六步，根据以上映射关系，参照原始图像中的像素，可以写出直方图均衡化之后的图像，如图7所示。

图 7 直方图均衡化之后的图像
以上过程即为手动计算直方图均衡化。接着，我们看一下均衡化后图像的灰度直方图，如图8所示。

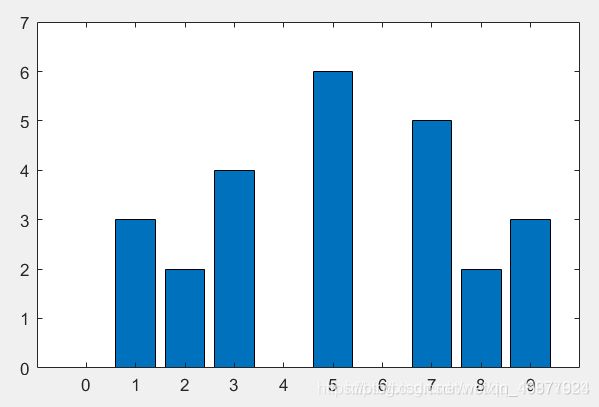
图 8 均衡化后图像的灰度直方图

根据图6和图8，说明一下直方图均衡化是如何增强图像对比度的。在图6中，原始图像灰度值为4，5，7的像素的个数为1，因此在图8中，这三个像素值点分别归并到相邻的灰度值中。因为有三个灰度值归并，因此在均衡化处理后，出现了三个空位，由这些空位将原来相邻的灰度值展开（举个例子：5和6相邻，均衡化后，变成5和7相邻），故而展宽了对比度，但是归并也带来了某些相邻像素对比度的降低（举个例子：4和5相邻，均衡化后，变成5和5相邻）。这也说明了直方图均衡化方法对灰度分布比较集中的图像的处理效果比较明显。

2.python实现直方图均衡化

3直方图均衡化的缺点

如果一幅图像整体偏暗或者偏亮，那么直方图均衡化的方法很适用。但直方图均衡化是一种全局处理方式，它对处理的数据不加选择，可能会增加背景干扰信息的对比度并且降低有用信号的对比度（如果图像某些区域对比度很好，而另一些区域对比度不好，那采用直方图均衡化就不一定适用）。此外，均衡化后图像的灰度级减少，某些细节将会消失；某些图像（如直方图有高峰），经过均衡化后对比度不自然的过分增强。针对直方图均衡化的缺点，已经有局部的直方图均衡化方法出现。

4.参考文献

1.Rafael C. Gonzalez, Richard E. Woods，Digital Image Processing (Third Edition)
2.胡学龙. 数字图像处理（第三版）
3.左飞. 图像处理中的数学修炼
4.https://blog.csdn.net/qq_15971883/article/details/88699218