二叉树进阶——迭代实现前中后序遍历
二叉树的递归遍历代码简单且容易理解,具体可以看这篇博客,里面的递归解释的较为详细
数据结构——二叉树的链式结构及实现(C语言)
然而现实生活中,一棵树的节点往往较多且深度更深时,如果继续使用递归就会产生较多的栈帧,导致栈溢出,对于Linux的进程地址空间来说,一个进程所分配的栈的空间大小是有限且较小的,因此这时候我们就需要使用迭代的方式来实现一棵树的遍历。
不过对于现代编译器而言,debug版本下的递归较大时会导致栈溢出,但是release版本编译器做了优化往往和迭代的效率差不多。
尽管这样,迭代方式还是要掌握的,尤其后序遍历是大厂面试的高频考点!
接下来由浅入深详细理解二叉树的迭代遍历!
一、前序遍历
1.1 问题描述
144. 二叉树的前序遍历
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
![]()
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
![]()
输入:root = [1,2]
输出:[1,2]
示例 5:
![]()
输入:root = [1,null,2]
输出:[1,2]
提示:
- 树中节点数目在范围
[0, 100]内 - `-100 <= Node.val <= 100
1.2 解题思路
首先回顾一下前序遍历的顺序是解题关键
- 先访问根节点
- 遍历访问左子树
- 遍历访问右子树
那么迭代实现二叉树三种遍历的话,都需要借助一个栈来保存树的节点,以便于回溯访问其它节点,定义一个cur指针指向当前节点。
注意:
栈中保存的是节点的指针而非val值,画图是为了方便理解不要产生误解
前序遍历迭代实现步骤:
-
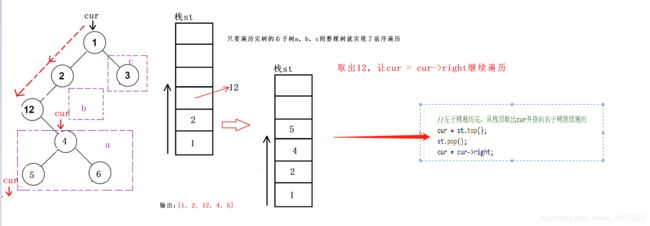
首先遍历树的左子树节点并依次保存到栈st中和数组中直到null停止,如下图所示,遍历并输出的左子树的顺序就是前序遍历的顺序

当这一步骤完成后我们会发现树的左子树全部访问完毕,只剩右子树没有访问了,这个时候我们区访问当前节点cur的右子树
简单来说,就是不断访问左子树入栈直到null,然后取栈顶元素出栈访问左子树为null的节点的右子树,将这个右子树的根节点作为当前节点继续访问左子树入栈。
上面叙述的1,2步骤代码实现简单,主要难点在于while主循环的结束条件
- cur不为空,cur不为空代表当前树还没有访问完,添加这个条件还有一个原因就是循环开始时栈为空,不能单纯以栈作为结束条件
- st栈不为空,栈不为空代表栈中还有数据没有访问完
具体代码如下,相信结合代码更容易理解
1.3 代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ret; //ret保存遍历结果
stack<TreeNode *> st; //st保存树的节点指针
TreeNode *cur = root; //cur指向当前遍历到的节点
//cur不为空代表树没访问完, st不为空代表栈中还有数据
while(cur || !st.empty())
{
//遍历左子树
while(cur)
{
st.push(cur); //当前节点入栈
ret.push_back(cur->val); //当前节点值保存到数组中
cur = cur->left; //继续遍历左子树
}
//左子树遍历完,从栈顶取出top并指向右子树继续遍历
TreeNode *top = st.top();
st.pop();
cur = top->right;
}
return ret;
}
};
如果理解了前序遍历,中序遍历就更容易实现了,只是简单访问位置的变化
二、中序遍历
1.1 问题描述
94. 二叉树的中序遍历
给定一个二叉树的根节点 root ,返回它的 中序 遍历。
示例 1:
![]()
输入:root = [1,null,2,3]
输出:[1,3,2]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
![]()
输入:root = [1,2]
输出:[2,1]
示例 5:
![]()
输入:root = [1,null,2]
输出:[1,2]
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
1.2 解题思路
中序遍历的解题思路和前序遍历相同,前序遍历是遍历左子树并入栈输出,中序遍历先遍历左子树并入栈直到null但不输出,当左子树访问完从栈顶取节点访问右子树时再打印即可,这正好符合了中序遍历的顺序
1.3 代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ret; //ret保存遍历结果
stack<TreeNode *> st; //st保存树的节点指针
TreeNode *cur = root; //cur指向当前遍历到的节点
//cur不为空代表树没访问完, st不为空代表栈中还有数据
while(cur || !st.empty())
{
//遍历左子树
while(cur)
{
st.push(cur); //当前节点入栈
cur = cur->left; //继续遍历左子树
}
//左子树遍历完,从栈顶取出cur并指向右子树继续遍历
cur = st.top();
st.pop();
ret.push_back(cur->val); //当前节点值保存到数组中
cur = cur->right;
}
return ret;
}
};
后序遍历
3.1 问题描述
145. 二叉树的后序遍历
给定一个二叉树,返回它的 后序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [3,2,1]
3.2 解题思路
后续遍历的顺序为
- 遍历访问左子树
- 遍历访问右子树
- 访问根节点
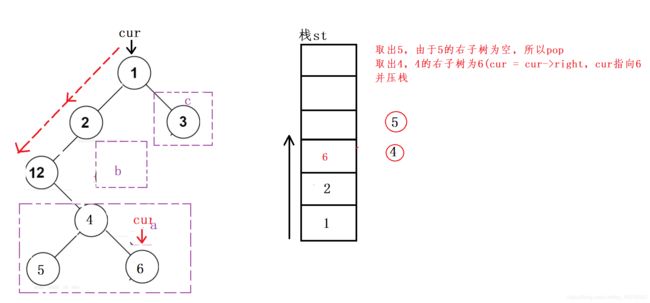
上面两个遍历的思路是遇到左子树为null压栈再访问右子树,无非就是访问的顺序不同
因为左节点只要不为null就会一直压栈,而后序遍历输出当前节点的标志就是左右子树都为null,这种情况表明节点左右子树为空已经遍历完了,访问根节点,符合后序遍历顺序
3.3 代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ret; //ret保存遍历结果
stack<TreeNode *> st; //st保存树的节点指针
TreeNode *prev = nullptr;
TreeNode *cur = root; //cur指向当前遍历到的节点
//cur不为空代表树没访问完, st不为空代表栈中还有数据
while(cur || !st.empty())
{
//遍历左子树
while(cur)
{
st.push(cur); //当前节点入栈
cur = cur->left; //继续遍历左子树
}
//左子树遍历完,从栈顶取出cur并指向右子树继续遍历
TreeNode *top = st.top();
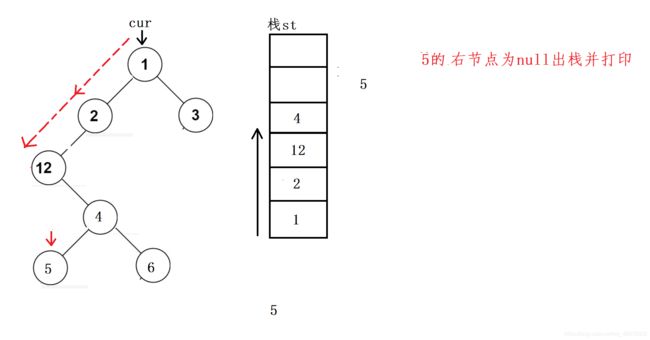
//右子树为null代表当前节点top左右子树都为空则输出,
//但是可能死循环,因为判断节点右子树时可能会被访问两次
//访问两次的标志就是当前节点的右树等于上一次访问的节点
if(top->right == nullptr || top->right == prev)
{
ret.push_back(top->val);
st.pop();
prev = top;
cur = nullptr;
}
else
{
cur = top->right;
}
}
return ret;
}
};