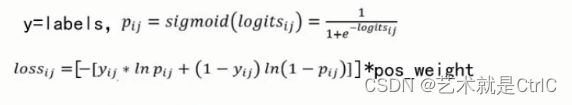TensorFlow入门(二十、损失函数)
损失函数
损失函数用真实值与预测值的距离指导模型的收敛方向,是网络学习质量的关键。不管是什么样的网络结构,如果使用的损失函数不正确,最终训练出的模型一定是不正确的。常见的两类损失函数为:①均值平方差②交叉熵
均值平方差
均值平方差(Mean Squared Error,MSE),也称"均方误差",在神经网络中主要用于表达预测值与真实值之间的差异,针对的是回归问题。其数学计算公式如下:
可以看出,均值平方差是对每一个真实值与预测值相减后的差的平方取平均值。在具体模型中,它的值越小,表明模型越好。除此之外,类似的损失算法还有均方根误差RMSE(即将MSE开平方)、平均绝对值误差MAD(对一个真实值与预测值相减的绝对值取平均值)等。
注意 : 在神经网络计算时,预测值要和真实值控制在同样的数据分布内,例如将预测值经过Sigmoid激活函数得到的值控制在0~1之间,那么真实值也需要归一化在0~1之间。这样,进行loss计算时才会有较好的效果。
在TensorFlow中,没有提供单独的MSE函数。由于公式简单,可以自己组合,例如:
MSE = tf.reduce_mean(tf.pow(tf.sub(logits,outputs),2.0))其中,logits代表标签值,即真实值,outputs代表预测值。
同理,均方根误差RMSE和平均绝对值误差MAD也可以手动组合,例如:
RMSE = tf.sqrt(tf.reduce_mean(tf.pow(tf.sub(logits,outputs),2.0)))
MAD = tf.reduce_mean(tf.complex_abs(tf.sub(logits,outputs)))交叉熵
交叉熵(crossentropy),一般针对的是分类问题,主要用于预测输入样本属于某一类的概率。其数学计算公式如下:
其中y代表真实值分类(0或1),a代表预测值。
注意 : 用于计算的a也是通过分布统一化处理的(或者是经过Sigmoid函数激活的),取值范围在0~1之间。如果真实值和预测值都是1,前面一项y*ln(a)就是1*ln(1)等于0,后一项(1-y)*ln(1-a)也就是0*ln(0)等于0,loss为0,反之loss函数为其他数。
在TensorFlow中常见的交叉熵函数有:
①Sigmoid交叉熵
Sigmoid交叉熵,即tf.nn.sigmoid_cross_entropy_with_logits(_sentinel = None,labels = None,logits = None,name = None),该函数对logits计算sigmoid的交叉熵。logits是神经网络模型中的w*x矩阵,也是神经网络最后一层的输出,还没有经过sigmoid激活函数计算,而labels是实际的标签值,它的shape和logits相同。
具体计算公式如下:
②softmax交叉熵
softmax交叉熵,即tf.nn.softmax_cross_entropy_with_logits(logits,labels,name = None),该函数的参数logits和labels,与Sigmoid交叉熵函数的一样。函数的计算过程一共分为两步:
①将logits通过softmax计算转换成概率,公式如下:
②计算交叉熵损失,把softmax的输出向量[y1,y2,y3...]和样本的实际标签做一个交叉熵,公式如下:
其中,y'i指代实际的标签中第i个的值,yi是上一步softmax的输出向量[y1,y2,y3...]中,第i个元素的值。非常明显,预测越准确,计算得出的值越小,最后再通过求平均值,得到最终的loss。注意:该函数的返回值是一个向量,不是一个数。
③sparse交叉熵
sparse交叉熵,即tf.nn.sparse_softmax_cross_entropy_with_logits(logits,labels,name = None),该函数用于计算logits和labels之间的稀疏softmax交叉熵。计算流程和softmax交叉熵一样,区别在于sparse交叉熵的样本真实值与预测结果不需要one-hot编码,但是要求分类的个数一定要从0开始。比如,如果分两类,标签的预测值只有0和1两个数。如果是五类,预测值有0,1,2,3,4共五个数。
④加权Sigmoid交叉熵
加权Sigmoid交叉熵,即tf.nn.weighted_cross_entropy_with_logits(targets,logits,pos_weight,name = None),该函数用于计算加权交叉熵。计算方式与Sigmoid交叉熵基本一样,只是加上了权重的功能,是计算具有权重的Sigmoid交叉熵函数。
计算公式如下:
使用时,直接调用对应的API即可。
小结
在实际的模型训练过程中,损失函数的选取取决于输入标签数据的类型:如果输入的是实数、无界的值,损失函数使用平方差;如果输入标签是位矢量(分类标志),使用交叉熵会更合适。