Leetcode: 236.二叉树的最近公共祖先
文章目录
- Leetcode:236.二叉树的公共祖先
-
-
- 题目描述
- 示例
- 思路分析
- 代码实现
-
Leetcode:236.二叉树的公共祖先
题目描述
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例
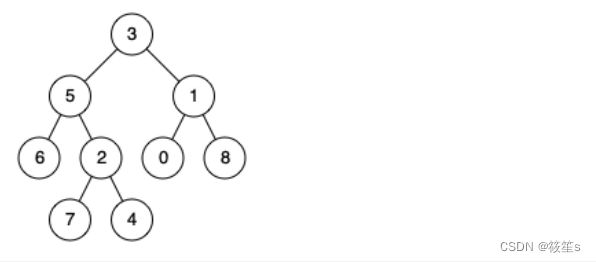
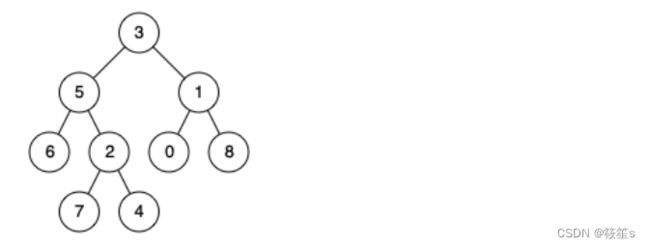
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例2
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3
输入:root = [1,2], p = 1, q = 2
输出:1
思路分析
规则:两个结点中,如果一个是左子树结点,一个是右子树结点,那么它就是公共祖先.
注意:如果两个结点中有一个结点为根结点,那么这个结点也为公共祖先.
解法一:
从根开始递归寻找,如果这两个结点在根的左右子树,就说明对于这棵树来说,这个根就为这两个结点的公共祖先,如果没找到,就说明此时p,q在这棵树根的同一子树中,此时有两种情况:
1:如果p,q结点在左子树,就重新递归到左子树寻找p,q的位置打是否在左子树根的一左一右.
2:如果p,q结点在右子树,就重新递归到右子树寻找p,q的位置是否在右子树根的一左一右.
查找函数:
1: 如果根为空,返回false.
2: 如果找到了,就返回true.
3: 如果没找到,就从root的左子树去找.
4: 左子树没找到就从root的右子树去找.
解法二:
a :我们可以采用类似前序遍历的方式利用栈来保存两个结点的祖先路径.
1: 如果为空树,就返回false.
2: 如果不为空,先入栈保存.
3: 如果找到了,就返回true.
4: 如果没找到,就递归从该树的左子树寻找,左子树没找到,就递归从该树的右子树寻找.
5:如果递归到一棵树的左右子树都为空,并且依旧还没找到,就说明这个结点root绝对不是目标结点的公共路径,所以要将这个结点出栈.并返回false.
b : 当得到两个结点的祖先路径,我们要将保存两个结点中祖先路径较长的栈出栈,直到和另一个栈的路径长度相等.( 出栈的结点一定没有公共祖先).
1:当两个保存祖先路径栈的长度相等,比较栈顶结点,如果相等则说明这个结点就为两个结点的公共祖先.
2:如果不相等则两个栈出栈继续比较栈顶元素,直到两个栈为空.
代码实现
解法一:
class Solution {
public:
bool find( TreeNode* sub,TreeNode* x )
{
if( sub == nullptr )
{
return false;
}
return ( sub == x ) || find( sub->left,x) || find( sub->right,x);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if( root == nullptr )
{
return nullptr;
}
if( root == p || root == q )
{
return root;
}
bool pInLeft,pInRight,qInLeft,qInRight;
pInLeft = find( root->left,p);
pInRight = !pInLeft;
qInLeft = find( root->left,q);
qInRight = !qInLeft;
if( pInLeft && qInRight || pInRight && qInLeft )
{
return root;
}
else if ( pInLeft && qInLeft )
{
return lowestCommonAncestor(root->left,p,q);
}
else if ( pInRight && qInRight )
{
return lowestCommonAncestor(root->right,p,q);
}
else{
return nullptr;
}
}
};
解法二:
class Solution {
public:
bool find( TreeNode* root, TreeNode* x, stack<TreeNode*>& path )
{
if( root == nullptr )
{
return false;
}
path.push(root);
if( root == x )
{
return true;
}
//如果左子树找到了就返回不再遍历
if( find( root->left,x,path) )
{
return true;
}
//如果左子树失败了,就从右子树找.
else if ( find( root->right,x,path))
{
return true;
}
else
{
//如果都没找
path.pop();
return false;
}
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack<TreeNode*> pPath,qPath;
find( root,p,pPath );
find( root,q,qPath );
//转换为链表相交,循环过后让两个祖先栈的路径长度相等.
while ( pPath.size() != qPath.size() )
{
if( pPath.size() > qPath.size() )
{
pPath.pop();
}
else
{
qPath.pop();
}
}
while( pPath.size() != 0 && qPath.size() != 0 )
{
if( pPath.top() == qPath.top() )
{
return pPath.top();
}
pPath.pop();
qPath.pop();
}
return nullptr;
}
};