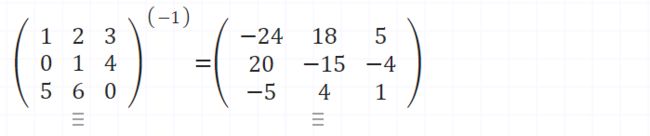关于SSA算法中矩阵的3种运算：转置、求逆、相乘
1、矩阵转置
// 矩阵转置(二维矩阵)
public static double[][] transposeTwo(double[][] matrix) {
int rows = matrix.length;
int cols = matrix[0].length;
double[][] transposedMatrix = new double[cols][rows];
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
transposedMatrix[j][i] = matrix[i][j];
}
}
return transposedMatrix;
}
矩阵转置测试：
package test;
public class transposeOne {
// 矩阵转置(二维矩阵)
public static double[][] transposeTwo(double[][] matrix) {
int rows = matrix.length;
int cols = matrix[0].length;
double[][] transposedMatrix = new double[cols][rows];
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
transposedMatrix[j][i] = matrix[i][j];
}
}
return transposedMatrix;
}
public static void printArray(double[][] array) {
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[i].length; j++) {
System.out.print(array[i][j] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
// 定义一个3x3的矩阵
double[][] matrixData1= {
{1, 2, 3},
{0, 1, 4},
{5, 6, 0}
};
double[][] f=transposeTwo(matrixData1);
printArray(f);
}
}
2、矩阵求逆
// 矩阵求逆（使用高斯-若尔当消元法）
public static double[][] matrixInverse(double[][] matrix) {
int n = matrix.length;
double[][] result = new double[n][n];
double[][] temp = new double[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
temp[i][j] = matrix[i][j];
}
}
for (int i = 0; i < n; i++) {
result[i][i] = 1;
}
for (int i = 0; i < n; i++) {
double diagonalElement = temp[i][i];
if (diagonalElement == 0) {
throw new IllegalArgumentException("Matrix is not invertible");
}
for (int j = 0; j < n; j++) {
temp[i][j] /= diagonalElement;
result[i][j] /= diagonalElement;
}
for (int k = 0; k < n; k++) {
if (k != i) {
double tempValue = temp[k][i];
for (int j = 0; j < n; j++) {
temp[k][j] -= tempValue * temp[i][j];
result[k][j] -= tempValue * result[i][j];
}
}
}
}
return result;
}
矩阵求逆测试
package test;
/**
* 求二维矩阵的逆矩阵
*/
public class test1 {
public static double[][] invert(double[][] matrix) {
int n = matrix.length;
double[][] result = new double[n][n];
double[][] temp = new double[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
temp[i][j] = matrix[i][j];
}
}
for (int i = 0; i < n; i++) {
result[i][i] = 1;
}
for (int i = 0; i < n; i++) {
double diagonalElement = temp[i][i];
if (diagonalElement == 0) {
throw new IllegalArgumentException("Matrix is not invertible");
}
for (int j = 0; j < n; j++) {
temp[i][j] /= diagonalElement;
result[i][j] /= diagonalElement;
}
for (int k = 0; k < n; k++) {
if (k != i) {
double tempValue = temp[k][i];
for (int j = 0; j < n; j++) {
temp[k][j] -= tempValue * temp[i][j];
result[k][j] -= tempValue * result[i][j];
}
}
}
}
return result;
}
public static void printArray(double[][] array) {
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[i].length; j++) {
System.out.print(array[i][j] + " ");
}
System.out.println();
}
}
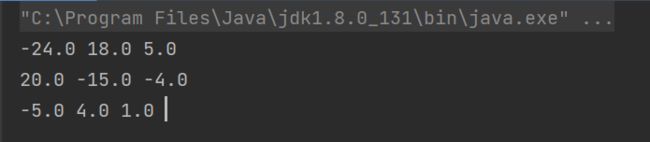
public static void main(String[] args) {
// 定义一个3x3的矩阵
double[][] matrixData = {
{1, 2, 3},
{0, 1, 4},
{5, 6, 0}
};
// 求矩阵的逆
double[][] result = invert(matrixData);
printArray(result);
}
}
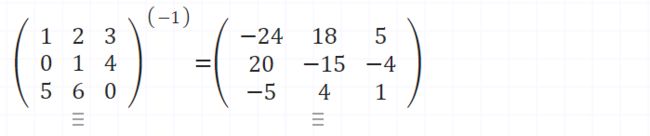
3、矩阵相乘
// 矩阵相乘
public static double[][] matrixMultiply(double[][] matrix1, double[][] matrix2) {
int rows1 = matrix1.length;
int cols1 = matrix1[0].length;
int rows2 = matrix2.length;
int cols2 = matrix2[0].length;
if (cols1 != rows2) {
throw new IllegalArgumentException("矩阵1的列数必须等于矩阵2的行数");
}
double[][] result = new double[rows1][cols2];
for (int i = 0; i < rows1; i++) {
for (int j = 0; j < cols2; j++) {
for (int k = 0; k < cols1; k++) {
result[i][j] += matrix1[i][k] * matrix2[k][j];
}
}
}
return result;
}
矩阵相乘测试：
package test;
public class test_matrixMultiply {
// 矩阵相乘
public static double[][] matrixMultiply(double[][] matrix1, double[][] matrix2) {
int rows1 = matrix1.length;
int cols1 = matrix1[0].length;
int rows2 = matrix2.length;
int cols2 = matrix2[0].length;
if (cols1 != rows2) {
throw new IllegalArgumentException("矩阵1的列数必须等于矩阵2的行数");
}
double[][] result = new double[rows1][cols2];
for (int i = 0; i < rows1; i++) {
for (int j = 0; j < cols2; j++) {
for (int k = 0; k < cols1; k++) {
result[i][j] += matrix1[i][k] * matrix2[k][j];
}
}
}
return result;
}
public static void printArray(double[][] array) {
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[i].length; j++) {
System.out.print(array[i][j] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
// 定义一个3x3的矩阵
double[][] matrixData1= {
{1, 2, 3},
{0, 1, 4},
{5, 6, 0}
};
double[][] matrixData2 = {
{1, 2, 3},
{0, 1, 4},
{5, 6, 0}
};
// 求矩阵的逆
double[][] result = matrixMultiply(matrixData1,matrixData2);
printArray(result);
}
}
